
- •Цепь переменного тока при последовательном соединении элементов
- •Цепь переменного тока при параллельном соединении элементов
- •Трехфазное соединение звездой с нейтральным проводом
- •Пример расчета трехфазной нагрузки, соединенной звездой с нейтральным проводом
- •Трансформаторы
- •Работа трансформатора под нагрузкой
- •Внешняя характеристика трансформатора
- •Механические характеристики эд и им
- •Устройство и принцип действия ад.
- •Основные уравнения ад
- •Момент вращения ад
- •Механическая характеристика ад
- •Регулирование скорости вращения ад
- •Способы пуска ад
- •2. Методы, основанные на сопротивления ротора r2
- •Устройство и принцип действия дпт.
- •Классификация дпт по способу возбуждения.
- •Принцип действия дпт.
Трехфазное соединение звездой с нейтральным проводом
В звезде с нейтральным проводом каждая фаза нагрузки с помощью нейтрального провода и соответствующей линии независимо подключена к своему генератору. Следовательно, если не учитывать малые падения напряжения в линии, фазные напряжения, также как ЭДС генератора равны по величине и сдвинуты по фазе на 1200.
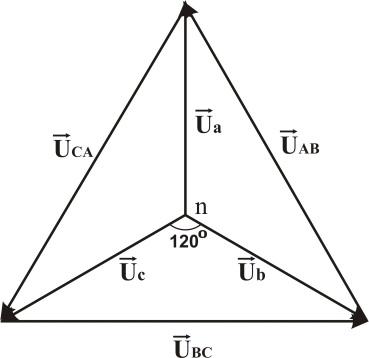
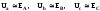
Соответственно, линейные напряжения
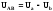

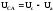
Из векторной диаграммы линейных и фазных напряжений можно найти соотношение между ними. По теореме косинусов для любого линейного напряжения (учитывая, что cos1200 = – 0.5) получим
 =
=

Следовательно, в звезде с
нейтральным проводом при любой нагрузке
линейные напряжения (Uл)
равны по величине и в
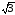 раз больше фазных (Uф).
раз больше фазных (Uф).
Uл
= UAB
= UBC
= UCA
=
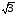 Uф
=
Uф
=
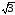 Ua
=
Ua
=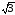 Ub
=
Ub
=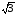 Uc
Uc
Из схемы соединения нагрузки звездой следует, что линейные токи равны соответствующим фазным
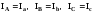
Ток в нейтральном проводе
можно определить из I
закона Кирхгофа для нейтральной точки
нагрузки “n”
 – сумма
геометрическая (векторная), следовательно,
для определения In
нужно построить векторную диаграмму.
– сумма
геометрическая (векторная), следовательно,
для определения In
нужно построить векторную диаграмму.
Пример расчета трехфазной нагрузки, соединенной звездой с нейтральным проводом
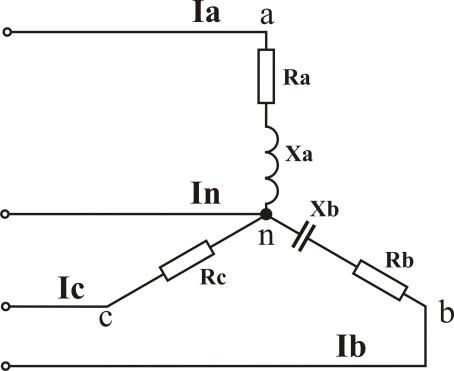
Пусть известно линейное напряжение и сопротивления
всех фаз
Определяем фазные напряжения
Ua
= Ub = Uc = Uл
/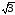
Определяем сопротивления фаз, фазные токи и углы сдвига фаз между током и напряжением
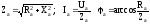
Аналогично определяются Zb, Ib, φb; Zc, Ic, φc
Ток в нейтральном проводе определяется по векторной диаграмме (ВД)
Порядок построения ВД
3.1.
Строим 3 вектора фазных напряжений
 со
сдвигом на 1200
со
сдвигом на 1200

 , учитывая
величину
и направление
угла сдвига фаз между током и напряжением.
, учитывая
величину
и направление
угла сдвига фаз между током и напряжением.
3.3.Складываем геометрически
фазные токи и находим ток
в нейтральном проводе

ФМС
ФМС служат для усиления магнитного поля и придания ему нужной конфигурации. При введении в катушку ФМС он намагничивается и его собственное магнитное поле складывается с полем катушки. В результате магнитный поток (МП) резко возрастает (приблизительно в раз).
– магнитная проницаемость ФМС (до 10 000).
Следовательно, используя ФМС, при том же токе в катушке можно получить в раз больший МП, или заданный МП получить при в раз меньшем токе в обмотке.
Это огромный плюс использования ФМС. Но есть и минусы.
–– В ФМС возникают дополнительные потери энергии (потери в стали)
Рст = Рвт + Рг
1. Вихревые потери Рвт – ток переменный => МП переменный, он будет в самом ФМС индуктировать ЭДС (закон Фарадея), сердечник проводящий, по нему текут вихревые токи, которые разогревают сердечник. Для уменьшения этих потерь сердечники делают не сплошными, а набирают из тонких изолированных пластин, или прессуют из ферромагнитного порошка с диэлектрическим связующим.
2. Гистерезисные потери Рг – или потери на перемагничивание. Ток переменный, при каждом изменении направления тока ФМС перемагничивается, на это тратится энергия, пропорциональная частоте и площади петли гистерезиса. Для уменьшения этих потерь ФМС изготавливают из магнито-мягких материалов с узкой петлей гистерезиса.
