3. Краткие теоретические сведения

Раздел 1. Вероятность и теоремы о ней

Множество всех взаимоисключающих друг друга исходов опыта называется пространством элементарных событий и обозначается Ω, т. е. Ω = {ω₁, ω₂, …}, где ω_i – элементарные события (исходы). Любое подмножество А множества Ω называется событием.

Суммой А + В событий А и В называется событие, состоящее из тех исходов, которые входят в событие А, или в событие В, или в то и другое.

Произведением АВ событий А и В называется событие, состоящее из исходов, которые входят в оба события А и В.

Разностью А – В событий А и В называется событие, состоящее из исходов, входящих в А, но не входящих в В.

Достоверным называется событие, состоящее из всех исходов и обозначается Ω. Событие, не содержащее исходов, называется невозможным и обозначается Ø. События, не содержащие общих исходов, называются несовместными, т. е. если А и В – несовместны, то АВ = Ø.

Событие состоящее из всех исходов опыта, не входящих в событие А, называется противоположным (дополнительным) событию А.

Если множество Ω состоит из n равновозможных исходов, то вероятность Р(А) события А равна

Р(А) = (1)

где m – число исходов, входящих в событие А («благоприятные» для А исходы).

Вероятность (1) называется классической.

Геометрическая вероятность попадания случайной точки в область g, являющейся частью области G, равна

Р(g) = (2)

где мера области – это либо длина, либо площадь, либо объем этой области.

Для вычисления числа исходов опыта (n и m) часто используют формулы комбинаторики.

Число всех перестановок Р_n множества из n равно

Р_n = n!. (3)

Число размещений из n элементов по k равно

(4)

Число сочетаний из n элементов по k равно

(5)

Условная вероятность Р(А | В) события А при условии, что событие В произошло, равна

(6)

где Р(В)  0.

События А и В называются независимыми, если выполняется условие

Р(АВ) = Р(А) ∙ Р(В). (7)

Для независимых событий справедливо

Р(А | В) = Р(А); Р(В | А) = Р(В). (8)

Свойства вероятности:

1. Р(Ω) = 1;

2. Р(Ø) = 0;

3. 0 ≤ Р(А) ≤ 1 для любого события А;

4. Р(А + В) = Р(А) + Р(В) – Р(АВ) для любых событий А и В. Если А и В – несовместны, то Р(А + В) = Р(А) + Р(В);

5. Р = 1 – Р(А);

6. Р(АВ) = Р(А) ∙ Р(В | А) = Р(В) ∙ Р(А | В) для любых событий А и В. Если А и В – независимые события, то Р(АВ) = Р(А) ∙ Р(В).

События H₁, H₂, …, H_n образуют полную группу событий, если они попарно несовместны и в сумме составляют достоверное событие, т. е.

H_i ∙ H_j = Ø (i ≠ j) и H₁ + H₂ + … + H_n = Ω. (9)

Вероятность события А, которое может наступить только вместе с одним из несовместных событий (гипотез) H₁, H₂, …, H_n, вычисляется по формуле полной вероятности:

Р(А) = (10)

С формулой (10) тесно связана формула Байеса, позволяющая вычислить новые условные вероятности гипотез H_i, при условии, что событие А наступило:

i = 1, 2, …, n, (11)

где Р(А) – полная вероятность (10).

Вероятность того, что в n независимых испытаниях успех наступит ровно m раз, находится по формуле Бернулли:

Р_n(m) = (12)

где – число сочетаний из n по m;

р – вероятность успеха в одном испытании;

q = 1 – р – вероятность неудачи.

Если число опытов n велико, а вероятность успеха р – мала (р < 0,1), то вместо формулы (12) применяют приближенную формулу Пуассона

Р_n(m) ≈ (13)

где λ = n ∙ p.

Формула (13) используется в задачах, относящихся к появлению редких событий.

Если m₁, m₂ – целые числа, такие, что 0 ≤ m₁ ≤ m₂ ≤ n, то вероятность того, что успех наступит не менее m₁ и не более m₂ раз в n испытаниях, находится по формуле

Р( m₁ ≤ m ≤ m₂) = 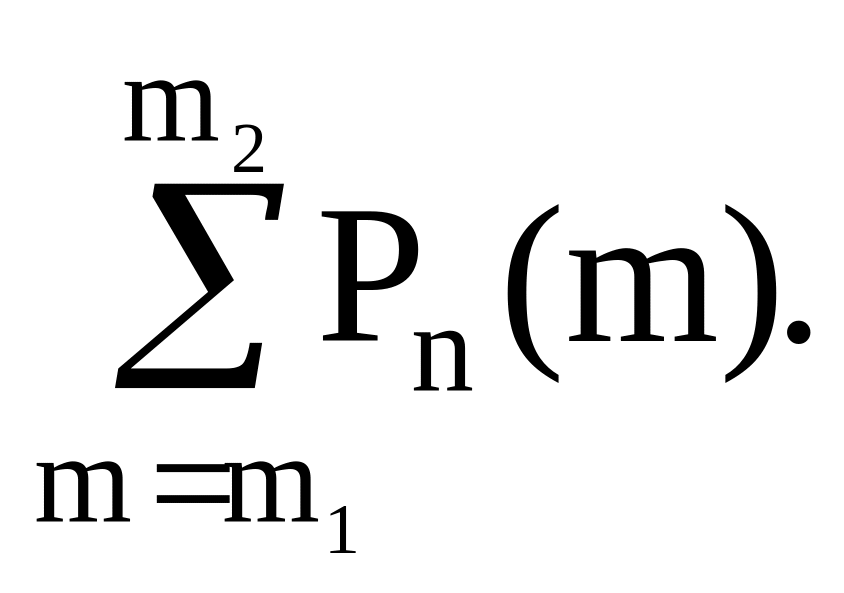(14)