8.4. Определение точек пересечения прямой линии с многогранником

В качестве примера рассмотрим определение проекции точек пересечения прямой l и многогранника SABCD. На рис. 8.7 показано наглядное изображение. Как видим из рисунка плоскость посредник расположена таким образом, чтобы ей принадлежала прямая l. Поэтом на линии пересечения многогранника и плоскости будут находиться точки пересечения прямой линии и многогранника.

Р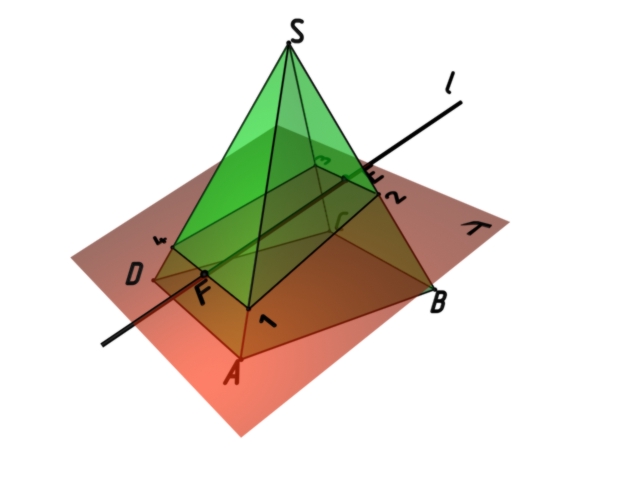 ис. 8.7

На рис. 8.8 показан комплексный чертеж определения точек пересечения пирамиды с прямой l. Показываем поверхность-посредник – фронтально проецирующую плоскость τ, проходящую через прямую l, – и определяем линию пересечения этой пирамиды плоскостью, которую решаем двумя способами: методом ребер для ребер SB, SC и SD находим фронтальные проекции точек пересечения ребер с плоскостью τ – 1₂, 2₂ и 3₂, а для проекций точек 4 и 5 – методом граней (линия пересечения основания пирамиды и проецирующей плоскости – фронтально проецирующая прямая 4–5).

Соединяем проекции горизонтальных точек пересечения – и получаем горизонтальную проекцию линии пересечения пирамиды с фронтально проецирующей плоскостью, в которой расположены прямая l и сечение.

Рис. 8.8

Точки пересечения пирамиды и прямой l определяем по горизонтальной проекции как проекции точек пересечения проекции прямой l с отрезками [12] и [45] – F и Е.

На горизонтальной проекции невидимая часть линии – E₁F₁, так как участки ребер 1S, 2S и 3S будут видимыми.

По горизонтальной проекции определяем, что точки прямой, находящиеся правее точки F, будут ближе, чем точки, принадлежащие пирамиде, а это значит, что на фронтальной проекции данного участка будет видна часть прямой l.

В качестве посредника не всегда использовать плоскости. В частности часто используют прямые линии, принадлежащие граням многогранника. На рис. 8.4 показан пример определения точки пересечения проецирующих прямых l и m с пирамидой.

Пример 30

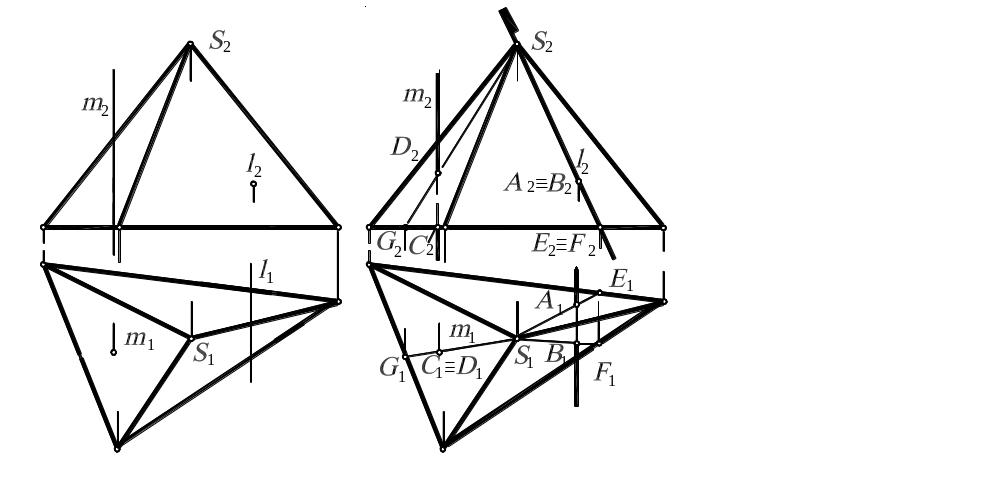
Задание: определить точки встречи прямых m и l с пирамидой и видимость участков прямой (рис. 8.9).

Решение: для прямой m (рис. 8.9) в качестве посредника удобно пользоваться прямой линией. Целесообразно на горизонтальной проекции провести проекцию прямой GS, проходящей через проекции вершины пирамиды S₁ и проекцию прямой m₁ и проекцию основания пирамиды G₁. Далее показываем фронтальную проекцию этой прямой и определяем проекцию верхней точки пересечения D₂. Проекция нижней точки C₂ находится на основании пирамиды. Используя линии связи, определяем горизонтальные проекции точек с и D.

а	б

Рис. 8.9

Для прямой l (рис. 8.9) целесообразно через фронтальную проекцию вершины пирамиды провести фронтально проецирующую плоскость, пересекающую основание пирамиды по фронтально проецирующей прямой, которой принадлежат точки Е и F. Пересечение треугольника E₁F₁S₁ и прямой l₁ определяет горизонтальные проекции точек А и В, которые будут точками пересечения прямой l и пирамиды. По линиям связи определяем фронтальные проекции этих точек. Видимость определяем известными способами.