8.1. Общие определения

М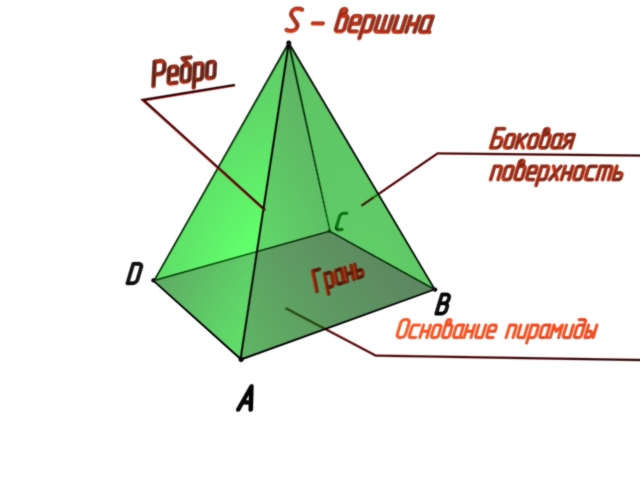 ногогранник – это пространственная фигура, образованная плоскими многоугольниками называемыми гранями. Линию пересечения плоских фигур называют ребрами, рис.8.1, комплексный чертеж, которой представлен на рис. 8.2

Рис. 8.1

Рис. 8.2

При конструировании многих инженерных сооружений, имеющих кривые поверхности, их часто заменяют (аппроксимируют) близкими по форме гранными поверхностями. Атомная структура металлических материалов имеет кристаллическую структуру, которая также имеет форму многогранников.

Рассмотрим те многогранники, которые чаще встречаются в деталях, а значит, на технических чертежах (рис. 8.1, 8.3).

Пирамидой называют многогранник, одна грань которого – многоугольник, являющийся основанием, а все остальные – треугольники с общей вершиной. Правильная пирамида имеет в основании правильный многоугольник, а высота (перпендикуляр, опущенный из вершины пирамиды на основание) проходит через центр этого многоугольника. На рис. 8.1 показано наглядное изображение пирамиды в аксонометрии, – ее проекции на рис. 8.2.

Призмой называют многогранник, две грани которого, называемые основаниями, – одинаковые многоугольники с взаимно параллельными сторонами, а все другие грани – параллелограммы. Призма называется прямой, если ее ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, то ее называют параллелепипедом. На рис. 8.3, а показана аксонометрическая проекция призмы, а на рис. 8.3, б – ее проекция.

a

б

Рис. 8.3

Как видно из комплексного чертеже обычно обозначают только верхние точки ребер призмы. Необходимо отметить, что для решения некоторых задач приходится мысленно увеличивать высоту призмы или пирамиды, поэтому эту часть будем считать мнимой.

Ч астным случаем призмы является куб – многогранник с одинаковыми квадратными гранями (рис. 8.4). если направление проецирование перпендикулярно грани куба, то на всех трех проекциях комплексного чертежа имеем одинаковые квадраты.

Рис. 8.4

8.2. Пересечение прямой и многогранника

Точки пересечения прямой и многогранника определяются способом вспомогательных поверхностей, рассмотренным при определении точки пересечения прямой и плоскости. В качестве поверхности-посредника выбираем проецирующую плоскость, проходящую через прямую, находим линию пересечения плоскости-посредника с многогранником и определяем общую точку сечения плоскости и прямой, которые и будут точками пересечения прямой с плоскостью. По известным правилам определяем видимость прямой. Пример определения точек пересечения прямой и многогранника будет рассмотрен ниже.

8.3. Определение линии пересечения многогранника с проецирующей плоскостью

Линия пересечения плоскости и многогранника определяется методом ребер или методом граней. Первый метод заключается в следующем: определяем точки пересечения проецирующей плоскости с ребрами многогранника (рис.8.4). Второй способ: определяем линии пересечения проецирующей плоскости и грани многогранника (рис.8.5).

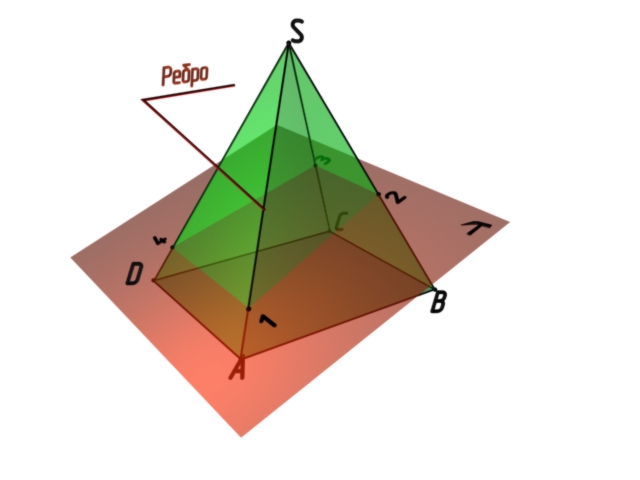
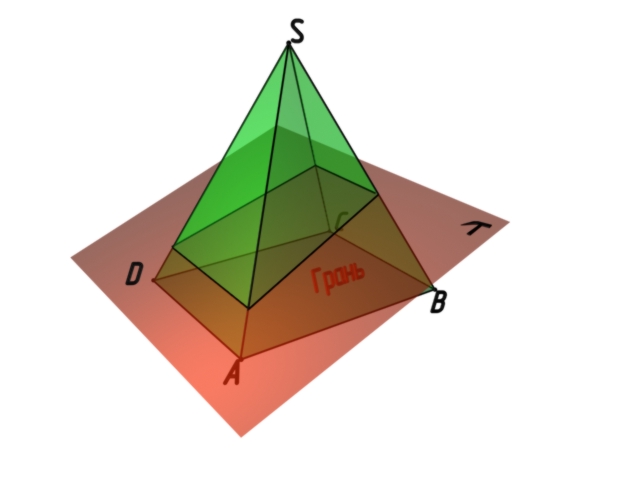
Рис. 8.4

Рис. 8.5

Пример 29

Задание:построить горизонтальную и профильную проекции линии пересечения пирамиды с плоскостью  (рис. 8.6).

Решение: решаем способом ребер

1 показываем фронтальные проекции точек пересечения ребер с плоскостью t.

2 по линиям связи определяем горизонтальные и профильные проекции точек пересечения

3 соединяем соответствующие проекции точек пересечения и показываем проекции линии пересечения одновременно обозначая видидмость.

Р ис. 8.6

При определении точек пересечения в качестве посредника выбирают проецирующую плоскость.