Плоскости уровня. Плоскость, параллельная плоскости проекций, называется плоскостью уровня. Плоскость проекций, которой параллельна плоскость уровня, дает название последней.

Горизонтальной плоскостью уровня называется плоскость, параллельная горизонтальной плоскости проекции (рис. 6.11, а). Эпюр этой плоскости показан на рис. 6.11, б. Обозначение буквой греческого алфавита Г и задана она в виде треугольника АВС. Анализируя рис. 6.11, можно сформулировать свойства такой плоскости: проекция горизонтальной плоскости уровня на фронтальную и профильную плоскости проекций изображается в виде прямой линии, а на горизонтальную плоскость проекций все фигуры, расположенные на горизонтальной плоскости уровня, будут проецироваться без искажения.

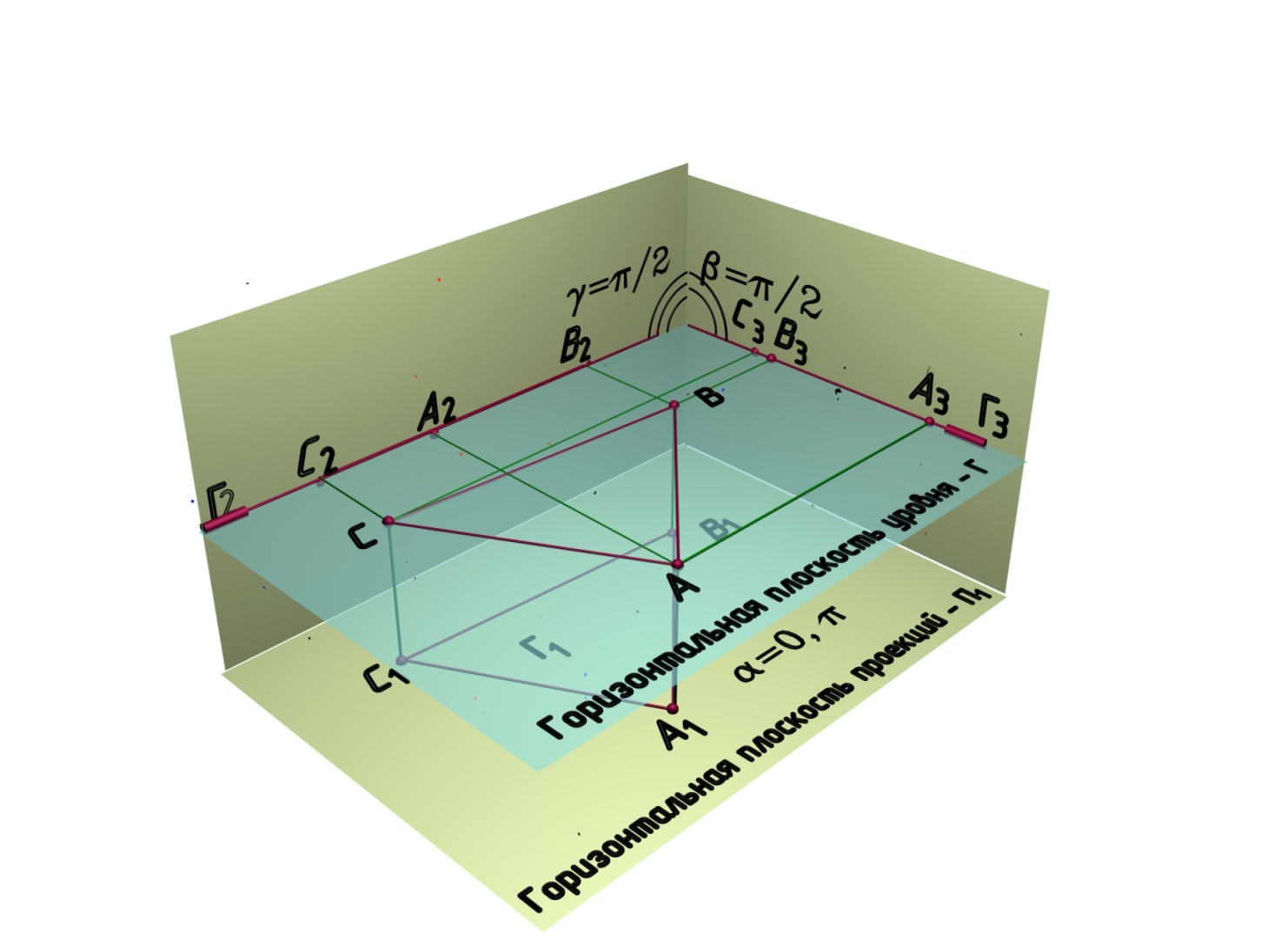
а

б

Рис. 6.11

Фронтальная плоскость уровня (плоскость, параллельная фронтальной плоскости проекций) показана на рис. 6.12. Это Ф(∆АВС). Свойства: проекция фронтальной плоскости уровня на горизонтальную и профильную плоскости проекций изображается в виде прямой линии, все плоские фигуры, расположенные на фронтальной плоскости уровня, будут проецироваться на фронтальную плоскость проекций без искажения. На рис. 6.12, а показано наглядное изображение фронтальной плоскости уровня, а на рис. 6.12, б – ее комплексный чертеж.

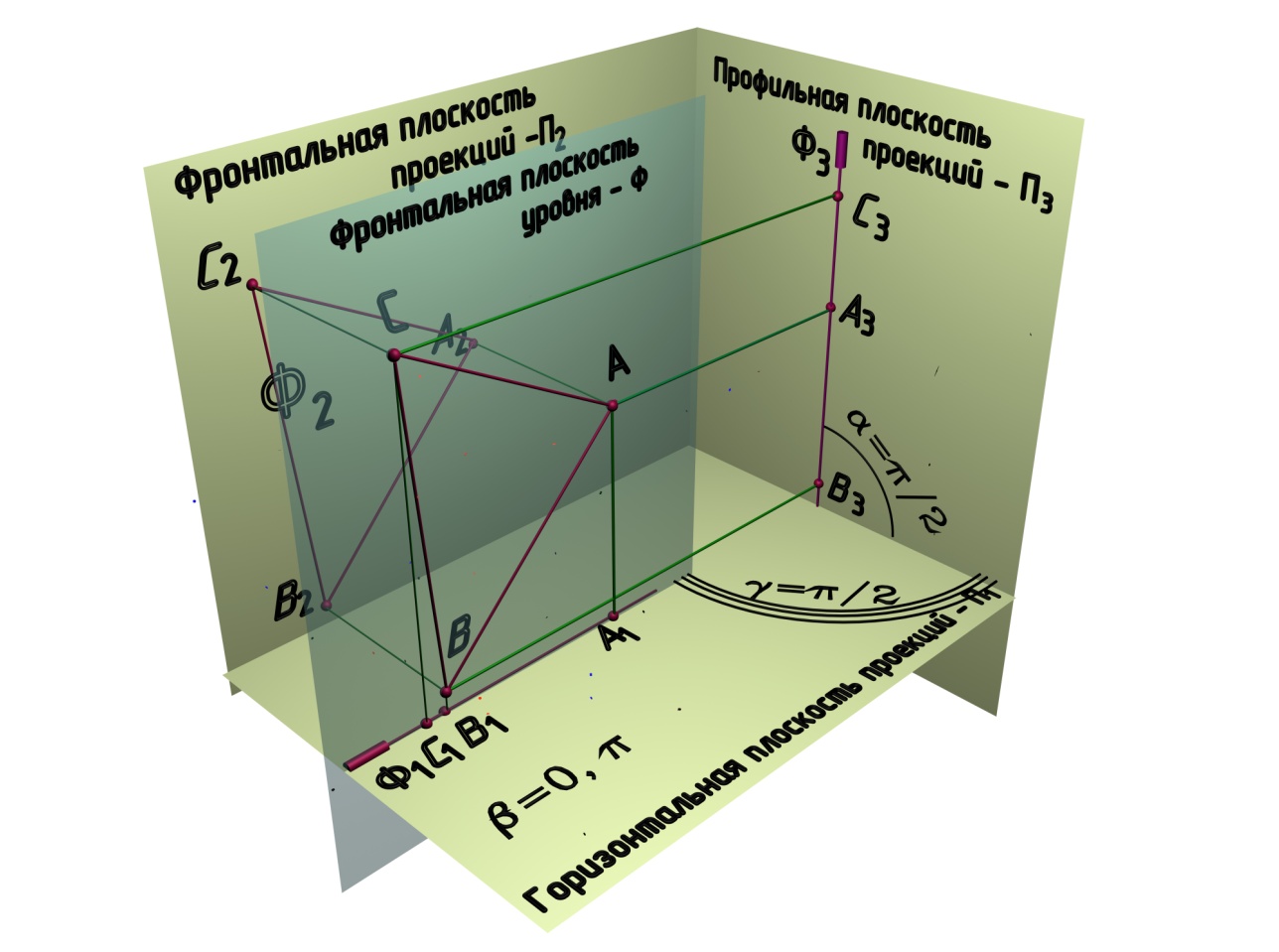
а

б

Рис. 6.12

П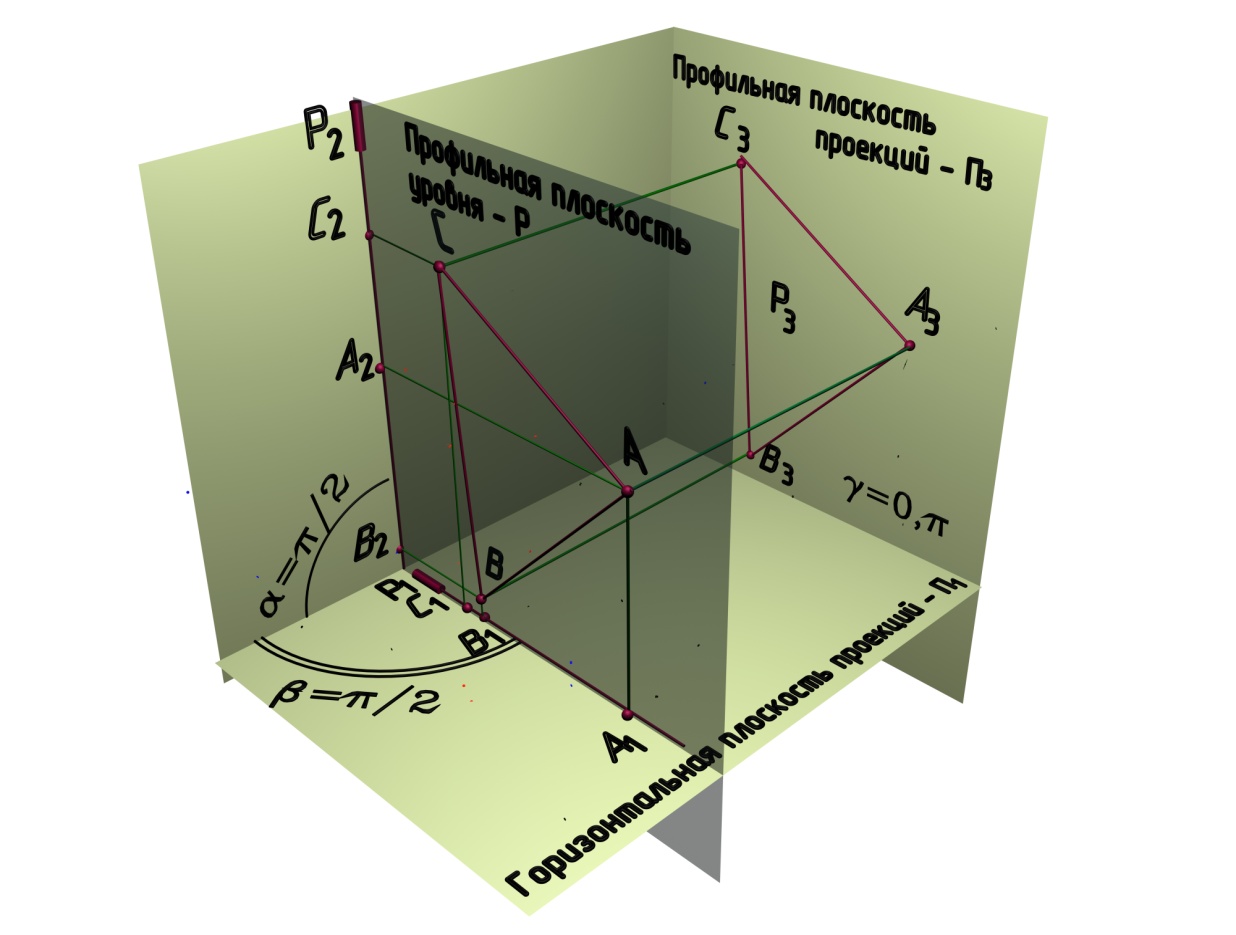 рофильная плоскость уровня – плоскость, параллельная профильной плоскости проекций, показана на рис. 6.13, а и на рис. 6.13, б – ее эпюр. Это Р(∆АВС). Свойства: проекция профильной плоскости уровня на горизонтальную и фронтальную плоскости проекций изображается в виде прямой линии, а на профильную плоскость проекций все фигуры, расположенные на профильной плоскости уровня, будут проецироваться без искажения.

а

б

Рис. 6.13

Понятие плоскостей частного положения имеет важное значение при дальнейшем изучении курса «Начертательная геометрия», в частности при определении линии пересечения поверхностей с помощью поверхностей-посредников.

6.4. Признак принадлежности точки и прямой плоскости

Признак принадлежности точки прямой был рассмотрен выше (свойство 1 евклидова пространства). Выбрать точку в плоскости, принадлежащей данной плоскости, произвольно, не связывая ее с другими элементами плоскости, невозможно. Точка в плоскости выбирается исходя из условия, что она находится на прямой линии этой плоскости. Так как все точки прямой, принадлежащей плоскости, принадлежат этой же плоскости, то решение задачи о принадлежности точки плоскости сводится к определению принадлежности прямой плоскости. Иными словами, признак принадлежности точки плоскости можно сформулировать следующим образом: точка принадлежит плоскости, если она принадлежит прямой, принадлежащей плоскости. Или точка принадлежит плоскости, если ее проекции принадлежат проекциям прямой, принадлежащей проекциям плоскости. На рис. 6.14, а показан комплексный чертеж из которого можно увидеть, что точка А принадлежит прямой точки а, а точка В – прямой b, что можно записать в виде математических формул

А₁ Î а₁ Ù А₂ Î а₂ А Î а; B₁ Î b₁ Ù B₂ Î b₂ B Î b

а	б

Рис. 6.14

Поскольку для определения положения прямой достаточно знать положение двух точек, принадлежащих прямой, то признак принадлежности прямой плоскости можно сформулировать так: если две точки прямой принадлежат плоскости, то и прямая принадлежит плоскости (рис. 6.14, б). Значит, если проекции двух точек прямой принадлежат проекциям точек плоскости, то прямая принадлежит плоскости. Для прямых c и d на рис. 6.14, б, можно записать как

1 Î d Ù b Ù 2 Î a Ù d d Î (a ´ b) и 4 Î с Ù b Ù 3 Î a Ù c c Î  (a ´ b).

Пример 20

Здание: построить проекции прямой a, принадлежащей ΔАBC (рис. 6.15).

Рис. 6.15

Решение: на любой из проекций проводим прямую а. В данном случае на горизонтальной проекции (рис. 6.16). По линиям связи определяем положение фронтальных проекций точек: 1 на стороне треугольника АС и 2 – ВС.

Так как на профильной проекции спроецировался в виде прямой линии (профильно проецирующаяся плоскость), проекции то все проекции любой линии принадлежащие плоскости будут лежать на этой прямой.

Рис. 6.16

Здесь же и будет располагаться третья проекция прямой линии. Поэтому отпадает необходимость нахождения проекций точек 1 и 2.