6.3. Способы задания плоскости на комплексном чертеже

По аналогии с прямой линией плоскости по отношению к плоскостям проекций могут располагаться так: а) произвольным образом – плоскости общего положения; б) перпендикулярно (проецирующие плоскости) или параллельно плоскости проекций (плоскости уровня) – плоскости частного положения. Указанная классификация плоскостей по положению относительно плоскостей проекций имеет принципиальное значение.

6.3.1. Плоскости общего положения

Из бесчисленного числа точек плоскости для ее однозначного определения на комплексном чертеже достаточно определить положение трех точек, принадлежащих плоскости и не лежащих на одной прямой (рис. 6.2, а). Этого будет достаточно для решения задач начертательной геометрии.

К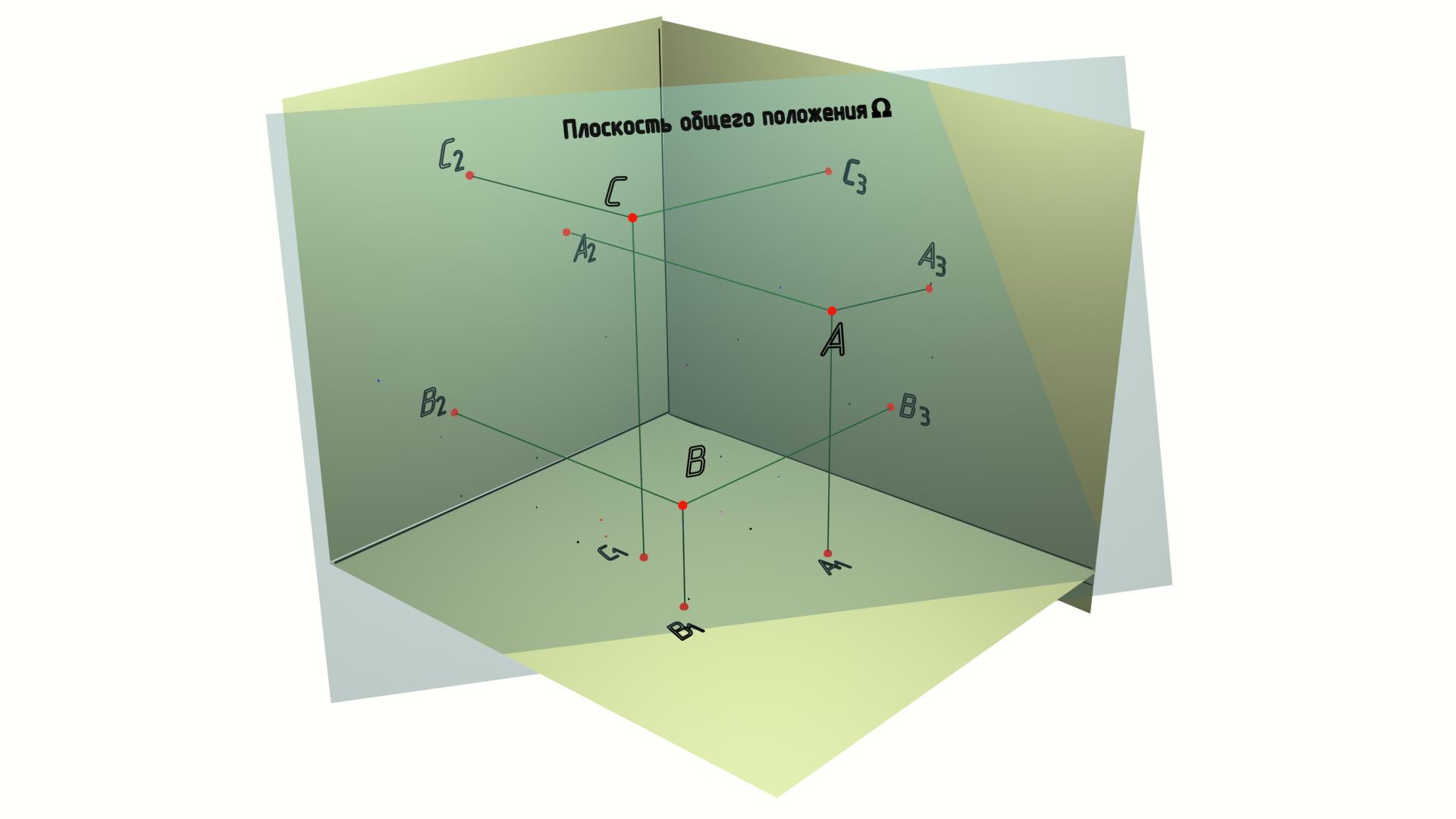 омплексный чертеж плоскости общего положения в виде проекций трех точек показан на рис. 6.2, б. Однако при решении той или иной задачи начертательной геометрии данный способ не всегда является рациональным и в зависимости от условия задачи его можно представить в другом виде.

а

б

Рис. 6.2

Рассмотрим какое сочетание простейших геометрических объектов (с точки зрения их построения) можно использовать для решения задач начертательной геометрии.

Н аиболее распространенный способ задания плоскости общего положения в виде треугольника (рис. 6.3). На рис. 6.3, а показан комплексный чертеж плоскости общего положения заданного в виде треугольника ((∆АВС)). Следует отметить, что при этом способе задания точки принадлежащие этой плоскости находятся не только внутри треугольника, но и снаружи. Иными словами мы должны видеть бесконечную плоскость.

а

б

Рис. 6.3

Следующий способ задания плоскости можно получить, если две точки представить в виде одной прямой (отрезка прямой) (рис. 6.4).

К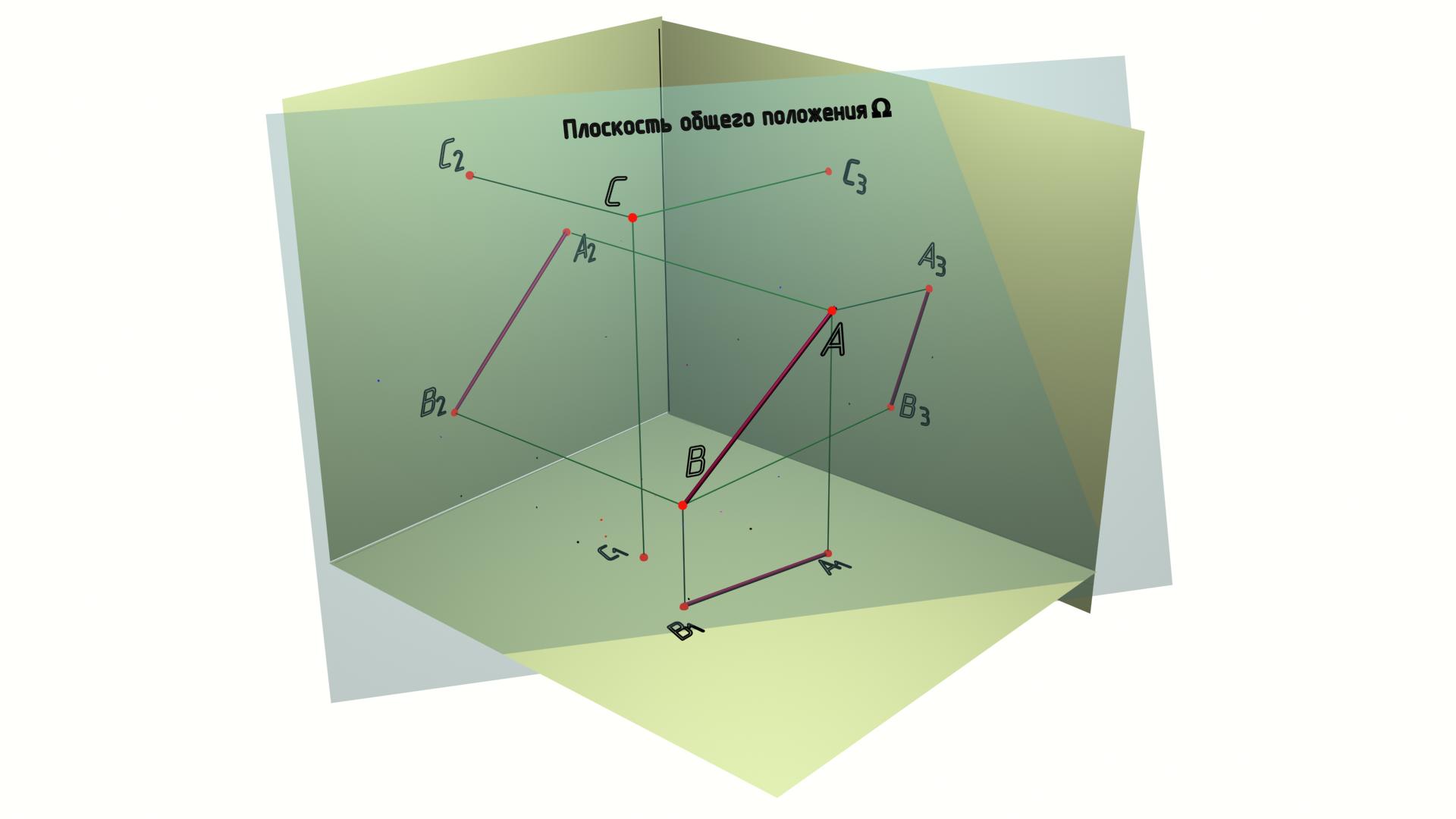 омплексный чертеж задания плоскости в виде отрезка и точки (С, [АВ]) показан на рис. 6.4.

а

б

Рис. 6.4

Если теперь через точку А провести параллельную прямую, то тогда ту же плоскость можно определить посредством двух параллельных прямых (рис. 6.5)

На основании свойства 6 п. 2.2.3 (проекции параллельных прямых параллельны) комплексный чертеж плоскости общего положения выглядит как проекции параллельных прямых (a ׀׀с) (рис. 6.5, б).

а

б

Рис. 6.5

Наконец, через три точки можно провести две пересекающиеся прямые (рис. 6.6), которые то же будут являться еще одним способом задания плоскостей. Комплексный чертеж плоскости общего положения, заданной в виде двух пересекающихся прямых (a  b) показан на рис. 6.6, б.

а

б

Рис. 6.6

Итак, мы рассмотрели четыре способа задания плоскости общего положения, основанных на проекциях трех точек. Именно, эти четыре способа подчеркивают свойство плоскости как поверхности первого порядка, что определяется прямыми линиями. Когда мы задаем плоскость тремя точками, то здесь обязательно должно быть пояснение, что это плоскость. В противном случае через три точки можно провести сколько угодно поверхностей порядок, которых будет выше первого. Однако, через три точки можно провести только одну плоскость.

Плоскости можно задавать на различных проекциях различными способами, как показано на рис. 6.7, где горизонтальная проекция задана в виде параллельных прямых

W₁(a₁ ׀׀ b₁), фронтальная – ₂(∆А₂В₂С₂) и профильная – ₃(С₃, [А₃В₃]).

Рис. 6.7

Однако, такова рода сочетание нескольких способов задания плоскостей практически не встречается.

Пример 19