Вопросы и задания для самопроверки

1. Как изображается прямая общего положения, как она располагается по отношению к плоскостям проекций? Показать на примере.

2. Какие существуют прямые частного положения?

3. Дать определение натуральной величины отрезка общего положения и определить углы наклона его к плоскостям проекций методом прямоугольного треугольника.

4. Дать определение натуральной величины и определить углы наклона к плоскостям проекций:

а) прямой уровня,

б) проецирующей прямой.

5. Перечислить возможные случаи расположения прямых в пространстве. И выполнить их комплексный чертеж.

6. Сформулируйте признак принадлежности точки прямой.

7. Сформулируйте признак пересечения прямых, опишите их свойства, выполните комплексный чертеж.

8. Сформулируйте признак параллельности прямых, опишите их свойства, выполните комплексный чертеж.

9. Сформулируйте признак скрещивающихся прямых, опишите их свойства, выполните комплексный чертеж.

6. Поверхности, плоскости

Наиболее сложным объектом для построения изображения является поверхность и ее частный случай – плоскость. При этом необходимо рассмотреть взаимодействие поверхностей с другими объектами: точкой, прямой, поверхностью.

6.1. Общие сведения

Все технические чертежи содержат проекции точек, линий и поверхностей, поэтому в начертательной геометрии необходимо рассматривать вопросы, связанные с изображениями поверхностей и способами их задания.

В начертательной геометрии поверхность может быть охарактеризована как совокупность всех последовательных положений образующей линии g вдоль неподвижных направляющих {d,….} линии g_j; указаний о характере перемещения g_j, при этом указания могут быть заданы также графически, в частности с помощью направляющей γ (рис. 6.1). Данный способ образования поверхности называется кинематическим. Существует каркасный способ задания поверхностей, когда поверхность задается в виде последовательного расположения линий d_i и ряда g_j, образующих сетку, или в виде последовательного положения узлов А_ij сетки:

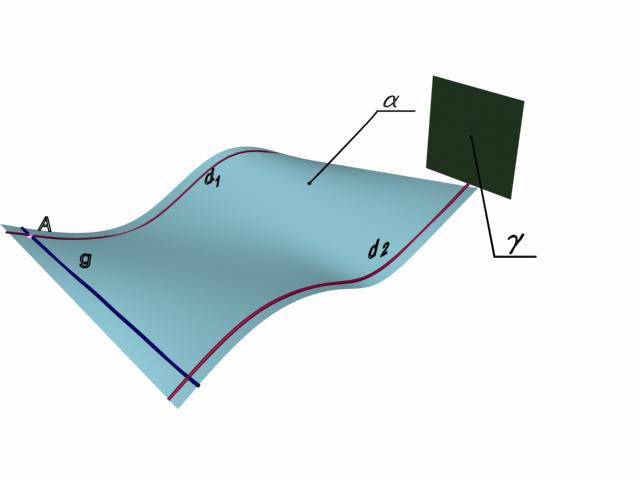
Рис. 6.1

Большое многообразие поверхностей, различные способы их формообразования, сложность геометрических характеристик создают трудности при попытках классифицировать поверхности, объединить их в систему.

Здесь мы рассмотрим три типа поверхностей: плоскости, многогранники и поверхности вращения, наиболее часто встречающиеся в технике

6.2. Определение плоскости

Если пользоваться приведенным выше определением поверхности, то плоскость можно рассматривать как совокупность всех последовательных положений прямой g вдоль двух параллельных линий d₁ и d₂. Если мы будем проецировать плоскость не перпендикулярно плоскости проекций, то проекции всех точек займут все поле чертежа (плоскость бесконечна).

Встает вопрос о способах задания плоскостей посредством минимального, но достаточного количества геометрических объектов, позволяющих решать композиционные и метрические задачи тем или иным способом. По отношению к плоскостям проекций плоскости могут занимать общее и частное положение.