Распознавание образов на Нейронной Сети Хопфилда.
Цель работы: Изучение особенностей применения НС Хопфилда для запоминания и восстановления искаженных образов.
Работа выполняется на программе MATLAB.
Время выполнения работы — 2 учебных часа
Методика выполнения работы.
Наибольшие трудности при распознавании возникают, когда подаваемый образ не полностью совпадает с эталонным образом. НС Хопфилда позволяет успешно решать задачи с неполной информацией за счет свойства ассоциативной памяти, которое присуще данной структуре сети.
При распознавании НС Хопфилда не определяет к какому классу относится предъявленный образ, а просто восстанавливает на своем выходе наиболее близкий к нему из уже запомненных образов. Поэтому если подать хранящийся в памяти НС образ, то она должна остаться в этом состоянии, а если подать на ее вход искаженный образ (зашумленный или затененный), то сеть перейдет к образу наиболее близкому (в смысле расстояния Хемминга) из запомненных.
Структура НС Хопфилда из S нейронов представлена на рис. 4.1, где w – матрица весовых коэффициентов размерностью [SxS], b – вектор смещения [Sx1], D – элементы задержки с внешним заданием состояния, на которые в первый момент времени поступают значения входного сигнала p (в нашем случае пикселей образа).
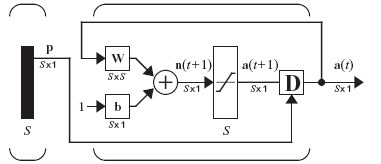
Рис. 4.1. Структура НС Хопфилда
Определим постановку задачи и последовательность ее решения на следующем примере. Требуется обучить НС для распознавания 10 букв английского алфавита, состоящие из 35 бит информации (7х5 пикселей).
Число нейронов в сети Хопфилда должно соответствовать числу бит информации в каждой букве. В данном случае число нейронов S равно 35. Для обучения НС Хопфилада необходимо сформировать входную обучающую матрицу из всех 10 образов, которые требуется запомнить (каждый образ представим в виде одного столбца в 35 элементов в матрице). В итоге получится матрица размерностью [35х10].
Замечание: НС Хопфилда функционирует с внутренними значениями переменных в диапазоне [-1, +1], поэтому исходное изображение необходимо нормировать из значений {0, 1} в {-1, +1}.
Для формирования входной матрицы символов воспользуемся встроенной функцией MATLAB prprob, которая возвращает матрицу 35х26, содержащую все буквы английского алфавита закодированные в виде столбцов из 35 элементов {-1, +1}.
Код MATLAB для создания массива для обучения приводится ниже.
% КОД 1.// Создание Обучающей выборки
[P,T] = prprob; % читаем матрицу всех символов
% P – матрица символов 35x26. 26 букв английского алфавита
% Каждая буква составляет вектор 35 элементов (5x7 пиксел).
% T - 26x26 единичная матрица. Не используется при обучении данной сети
[Nn, Np] = size(P); % размерность исходной матрицы
Nv = 1; % номер варианта.
Np = 10; % задаем число образов.
% выбираем Np букв в зависимости от номера варианта.
P = (2*P(:,Nv:(Nv+Np-1)-1); % переводим данные из {0 1} в {-1 +1}
Создание и обучение НС Хопфилда осуществляется с помощью функции newhop, в которую передается матрица запоминаемых образов размерностью [35x10].
% КОД 2.// Создание и обучение НС
net = newhop(P);
Замечание: В MATLAB для обучение НС Хопфилда используют алгоритмы обучения основанные на SVD разложении.
Для оценки работоспособности сети необходимо протестировать ее при подаче на вход искаженных образов. Рассмотрим влияние основных видов возможных искажений.
Первый вид шума - аддитивный, т.е. к каждому исходному образу P(:,p) добавляется случайный шум в диапазоне [-1 +1].
% КОД 3.// тестирование на образах с аддитивным шумом c ограничением +/-1
LevNoise = 50; % амплитуда аддитивного шума в процентах (%)
YS = zeros(35,Np);
for p = 1:Np
% читаем пример P(:,p), добавляем шум и ограничиваем результат [-1 1]
Y = satlins(P(:,p) + 2*(0.5-rand(Nn,1))*LevNoise/100);
% рисуем искаженный образ
figure(2+p),subplot(1,2,1),imagesc(reshape(Y, 5, 7)')
% выполняем 15 тактов функционирования сети
for i = 1:15, Y = sim(net,1,[],Y); end
% рисуем ближайший образ
figure(2+p),subplot(1,2,2),imagesc(reshape(Y, 5, 7)'), colormap('gray')
YS(:,p) = Y; % сохраняем результат
end
Error = sum(sum(abs(P-YS))) % вычисляем ошибку
Второй вид шума - зашумление, т.е. в исходном образе в N случайных точках (пикселях) их значения меняются на +1.
% КОД 4.// тестирование на зашумленных образах (добавляются точки +1)
NumPoint = 3; % количество точек зашумления
LevNoise = NumPoint/35
YS = zeros(35,Np);
for p = 1:Np
% читаем пример P(:,p), добавляем шум и ограничиваем результат [-1 1]
noise = 2*randerr(1,35,NumPoint)'; % создаем матрицу шума Np x 35
Y = satlins(P(:,p) + noise) ;
% рисуем искаженный образ
figure(2+p),subplot(1,2,1),imagesc(reshape(Y, 5, 7)')
% выполняем 15 тактов функционирования сети
for i = 1:15, Y = sim(net,1,[],Y); end
% рисуем ближайший образ
figure(2+p),subplot(1,2,2),imagesc(reshape(Y, 5, 7)'), colormap('gray')
YS(:,p) = Y; % сохраняем результат
end
Error = sum(sum(abs(P-YS))) % вычисляем ошибку
Третий вид шума - затенение, т.е. в исходном образе в N случайных точках (пикселях) их значения меняются на -1.
% КОД 5.// тестирование на затененных образах (добавляются точки -1)
NumPoint = 3; % количество точек затенения
LevNoise = NumPoint/35
YS = zeros(35,Np);
for p = 1:Np
% читаем пример P(:,p), добавляем шум и ограничиваем результат [-1 1]
noise = -2*randerr(1,35,NumPoint)'; % создаем матрицу шума Np x 35
Y = satlins(P(:,p) + noise) ; % читаем p пример + шум
% рисуем искаженный образ
figure(2+p),subplot(1,2,1),imagesc(reshape(Y, 5, 7)')
% выполняем 15 тактов функционирования сети
for i = 1:15, Y = sim(net,1,[],Y); end
% рисуем ближайший образ
figure(2+p),subplot(1,2,2),imagesc(reshape(Y, 5, 7)'), colormap(gray)
YS(:,p) = Y; % сохраняем результат
end
Error = sum(sum(abs(P-YS))) % вычисляем ошибку
Результатом выполнения данного кода является Np рисунков (для каждой буквы), на которых отображаются искаженные образы и ответ НС Хопфилда. Например, на рис. 4.2 приведены зашумленные и восстановленные образы, полученные в результате тестирования НС Хопфилда, описанные в кодах 3 (LevelNoise = 150%), 4 (LevelNoise = 8,57%), 5 (LevelNoise = 8,57%) для буквы «А» при Np = 10.
Рис. 4.2. Результаты тестирования НС Хопфилда для различных видов искажений: а) аддитивный шум, б) зашумление - добавляются точки +1, в) затенение –добавляются точки -1.
Дополнительно в командном окне отображается значение ошибки Error, которая считается как абсолютная разница между исходной и результирующей матрицами образов.
Номер варианта задается преподавателем и может быть {1,2,3,4,5,6,7,8,9,10,11}. В коде 1 присвоить Nv = номеру варианта.
Задание
1. Составить программу из кодов 1, 2, 3 при аддитивном шуме. Для различного количества запоминаемых образов Np={5,10,15} определить максимальный уровень шума из заданных значений LevelNoise = {50 100 150 200 250}, при котором сохраняется полное распознавание, т.е. Error < 1.
2. Составить программу из кодов 1, 2, 4 при зашумлении образа. Для различного количества запоминаемых образов Np={5,10,15} определить максимальный уровень шума из заданных значений NumPoint = {1 2 3 4 5}, при котором сохраняется полное распознавание, т.е. Error < 1.
3. Составить программу из кодов 1, 2, 5 при затенении образа. Для различного количества запоминаемых образов Np={5,10,15} определить максимальный уровень шума из заданных значений NumPoint = {1 2 3 4 5}, при котором сохраняется полное распознавание, т.е. Error < 1.
Отчет должен содержать: для каждого пункта и для каждого значения Np максимальный уровень шума.
Контрольные вопросы
1. Какие методы обучения НС Хопфилда знаете?
2. Как влияет число запоминаемых образов на распознающую способность сети Хопфилда?
3. Как определить, что НС Хопфилда закончила свою работу?
4. Что понимается под ассоциативной памятью с точки зрения работы НС Хопфилда?