Классификация на многослойной нейронной сети прямого распространения
Цель работы: Изучение особенностей применения МНСПР для классификации и способов формирования примеров для бинарной классификации.
Работа выполняется на программе MATLAB.
Время выполнения работы — 2 учебных часа.
Методика выполнения работы.
Бинарная классификация — частный случай распознавания образов, когда входные данные могут принадлежать только двум классам. Далее эти два класса будем называть “один” и “два”. Для бинарной классификации используют структуру МНСПР приведенную на рис. 2.1.
Рис. 2.1. Структура входов и выходов МНСПР для решения задачи бинарной классификации
Для данной задачи входной набор образов можно представить матрицей I, которая имеет размерность RxNp, где R — число признаков образа, Np—число образов. Эталонный выход можно представить вектором O, который имеет размерность 1xNp и принимает значения {-1 1}.
В данной работе исследуются функциональные возможности МНСПР в зависимости от её размерности на примере бинарной классификации двухмерного входного вектора.
Последовательность создания м-файла покажем для решения задачи классификации линейно-разделимых входных данных. Создадим случайные входные данные по x, y в диапазоне [- ].
% КОД 1// Создание случайных входных данных
Np = 5 % Количество примеров
x = 2*pi*(0.5-rand(Np)); % входная матрица X (Np x Np)
y = 2*pi*(0.5-rand(Np)); % входная матрица Y (Np x Np)
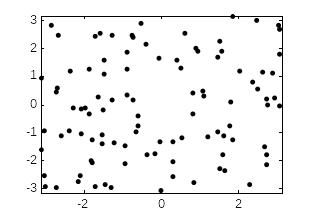
figure(1), plot(x,y,'k.'),axis([-pi pi -pi pi]) % область просмотра
Результатом выполнения данного кода показан на рис. 2.2 а. Функция axis ограничивает область просмотра в диапазоне [- ].
Определим принадлежность входных данных к классам {-1 1} по формуле z = sign(y – f(x)), где f(x) = 1.5*x+1.5 и описывает прямую проходящую через плоскость.
% КОД 2.// Формирование выходных данных (классов)
K=1.5; % (по № варианта)
f = @(x) (K*x + K); % описание функции границы классов
z = sign(y-f(x)); z(find(z >= 0)) = 1; % определяем классы {-1 +1}
i1 = find(z >= 0); i2 = find(z<0); % находим индексы для класса 1 и 2
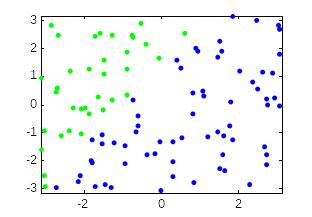
figure(1), plot(x(i1),y(i1),'g.',x(i2),y(i2),'b.'), axis([-pi pi -pi pi]) % область просмотра
Функция find возвращает вектор индексов i1 и i2, удовлетворяющих условию принадлежности к классам. Отразим на рисунке значения входных векторов с индексами i1 точечными маркерам зеленого цвета, входных векторов с индексами i2 маркерам синего цвета (рис. 2.2 б).
На основании входных и выходных данных необходимо сформировать обучающую выборку Ii = {xi, yi} Oi = {zi}, где i=1,…,Np*Np.
% КОД 3.// Создание обучающей выборки
I = [x(:) y(:)]'; % переводим все вх данные в размерность 2хNp
O = z(:)'; % переводим все значения классов в размерность 1хNp
а) б)
Рис.2.2. Результат выполнения кода 1(а) и кода 2 (б)
Для классификации линейно-разделимых данных достаточно использовать однослойную НС. Формально выходной нейрон должен иметь релейную характеристику, но тогда невозможно будет использовать алгоритмы обучения, основанные на вычислении градиента, поэтому функция преобразования выбирается tansig, которая удовлетворяет требованиям по обучению и близка к релейной. При обучении будем использовать метод trainlm, который обладает высокой скоростью сходимости.
% КОД 4.// Создание и Обучение НС
net = newff(minmax(I), [1],{'tansig'},'trainlm');
net.trainParam.epochs = 150;
net.trainParam.goal = 1e-10;
net=train(net,I,O);
Если после обучения достигнута желаемая точность, то НС теперь способна решать задачу классификации. Для проверки свойств обобщения НС создадим тестовую выборку, охватывающую все возможные значения x, y по заданной сетке в диапазоне [- ] c шагом 0.1. Функция meshgrid формирует матрицы х и у в заданном диапазоне.
% КОД 5// Создание тестовой выборки
[x, y] = meshgrid(-pi:0.1:pi); % формируем сетку
z = sign(y-f(x)); z(find(z >= 0)) = 1; % определяем классы {-1 +1}
I = [x(:) y(:)]'; % переводим все входные данные в размерность 2хNp
Подадим тестовые данные на НС и отобразим результаты классификации по аналогии с кодом 2. Для визуального сравнения с желаемым разбиением входных данных на этом же рисунке покажем эталонную функцию f(xe), которую нарисуем красной линией.
% КОД 6// Тестирование НС, отображение результатов классификации
out_nn = sign(sim(net, I)); % переводим выход НС в {-1, +1}
i1 = find(out_nn >= 0); i2 = find(out_nn < 0); % находим индексы для класса 1 и 2
xe = -pi:0.1:pi;
figure(2), plot(x(i1),y(i1),'g.', x(i2),y(i2),'b.', xe, f(xe), 'r-'), axis([-pi pi -pi pi])
E = sum(1-z(:).*out_nn')/2 % количество неверно распознаных
title(['Error: ' num2str(E)])
Для численной оценки посчитаем количество неверно распознанных входных данных E и отобразим полученное значение в заголовке на рисунке с помощью функции title. Результат тестирования имеет вид представленный на рис. 2.3, где красная линия – желаемое разделение.
Для однослойной НС можно посмотреть полученную функцию разделения
%ye = -net.IW{1,1}(1)/net.IW{1,1}(2)*xe - net.b{1}/net.IW{1,1}(2);
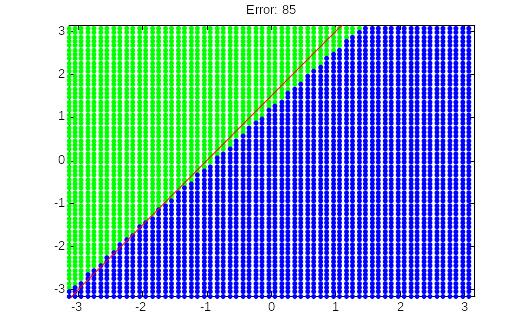
Рис.2.3. Результат тестирования НС
Таблица 2.1
№ вар |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
K |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
-1 |
-2 |
-3 |
Задание 1. Исследовать обобщающие способности НС для линейного разделения классов.
Составить программу в MATLAB состоящую из кодов 1-6.
Задать в коде 2 K из таблицы 1 в соответствии с номером варианта.
Изменяя количество примеров Np = {5, 10, 15, 20, 30, 40} оценить влияние случайной выборки на качество классификации визуально и на основании количество неверно распознанных входных данных E. Для каждого значения Np повторить расчет 3 раза и вычислить среднее значение Eav = (E1+E2+E3)/3.
Отчет по заданию 1 должен содержать текст программы, рисунки для пункта 3 при значение Np={5, 40}, Eav для каждого значения Np.
Задание 2. Исследовать обобщающие способности НС для нелинейного разделения классов.
Составить программу в MATLAB состоящую из кодов 1-6.
Заменить в коде 2 функцию разделения классов f = @(x) (K*sin(x));
Задать в коде 2 K из таблицы 1 в соответствии с номером варианта.
Добавить скрытый сдой нейронов в задании НС, т.е. в коде 4 изменить задание НС на следующую строку
net = newff(minmax(I), [N 1],{'tansig' 'tansig'},'trainlm');
Задать Np = 50 и подобрать минимальное количество нейронов в скрытом слое N.
Изменяя количество примеров Np = {5, 10, 15, 20, 30, 40} оценить влияние случайной выборки на качество классификации визуально и на основании количество неверно распознанных входных данных E. Для каждого значения Np повторить расчет 3 раза и вычислить среднее значение Eav = (E1+E2+E3)/3.
Отчет по заданию 2 должен содержать текст программы, рисунок для пункта 6, минимальное количество нейронов в скрытом слое, Eav для каждого значения Np.
Контрольные вопросы:
1. Какая минимальная структура НС способна реализовать линейное разделение входных данных?
2. Что такое бинарная классификация и какая структура МНСПР должна быть для решения данной задачи?
3. Что такое n-нарная классификация и какая структура МНСПР должна быть для решения данной задачи?
4. Как влияет количество скрытых слоев МНСПР на возможности классификации?
Лабораторная работа № 3