
- •Часть I
- •§ 1. Тригонометрия.
- •Радианная мера угла.
- •Тригонометрические величины некоторых углов.
- •Выражение одних тригонометрических функций через другие.
- •Формулы приведения.
- •Значения обратных тригонометрических функций некоторых углов.
- •Формулы решения простейших тригонометрических уравнений.
- •Частные случаи простейших тригонометрических уравнений.
- •§ 2. Таблица квадратов натуральных чисел от 10 до 99.
- •§ 3. Формулы преобразования многочленов.
- •Формулы сокращённого умножения.
- •Следствия из формул сокращённого умножения.
- •§ 4. Средние величины.
- •Неравенства между средними величинами:
- •§ 5. Модуль и его свойства.
- •§ 6. Степени и корни.
- •§ 7. Арифметическая прогрессия.
- •§ 8. Геометрическая прогрессия.
- •§ 9. Область определения функции.
- •§ 10. Множество значений функции.
- •§ 11. Чётность, нечётность, периодичность функции.
- •§ 12. Производная функции.
- •§ 13. Первообразная функции.
- •§ 14. Показательная функция.
- •§ 15. Логарифмы и логарифмическая функция.
- •§ 17. Графики элементарных функций.
- •§ 16. Факториал и его свойства.
- •§ 17. Основные математические постоянные.
- •§ 18. Конечные числовые суммы.
- •§ 19. Часто используемые неравенства.
- •400002, Волгоград, Университетский пр-т, 26
§ 17. Графики элементарных функций.
П
 рямая
пропорциональность задается формулой
рямая
пропорциональность задается формулой
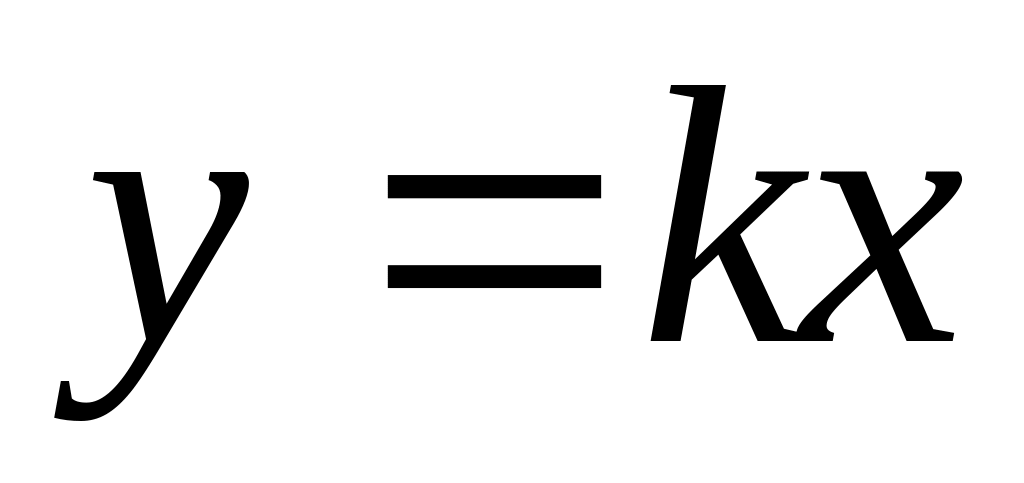 .
Графиком является прямая, проходящая
через начало координат и образующая с
осью
угол
,
причем
.
Графиком является прямая, проходящая
через начало координат и образующая с
осью
угол
,
причем
![]() ,
где
,
где
- угловой коэффициент прямой.
Линейная функция. Графиком линейной функции является прямая.
 - общий вид уравнения прямой с угловым
коэффициентом.
- общий вид уравнения прямой с угловым
коэффициентом.
При
![]() функция возрастает, при
функция возрастает, при
![]() убывает.
убывает.
- прямая, параллельная оси .
![]() - прямая, параллельная оси
.
- прямая, параллельная оси
.
![]() - уравнение оси
.
- уравнение оси
.
![]() - уравнение оси
.
- уравнение оси
.
Квадратичная функция , . Графиком квадратичной функции является парабола. При ветви параболы направлены вверх, при ветви направлены вниз. Количество корней уравнения зависит от дискриминанта
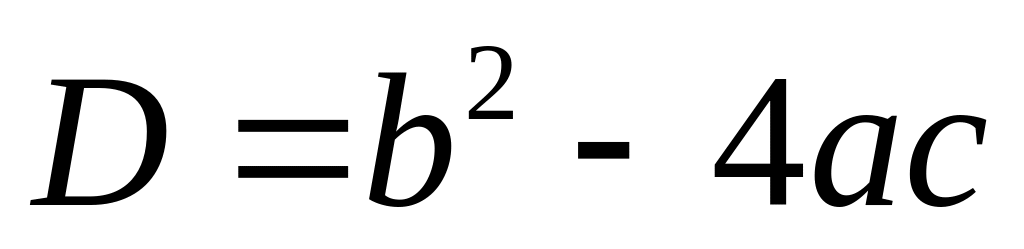 .
.
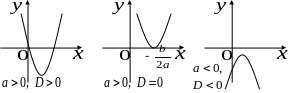
О
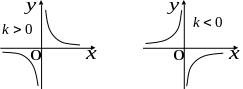 братная
пропорциональность
братная
пропорциональность
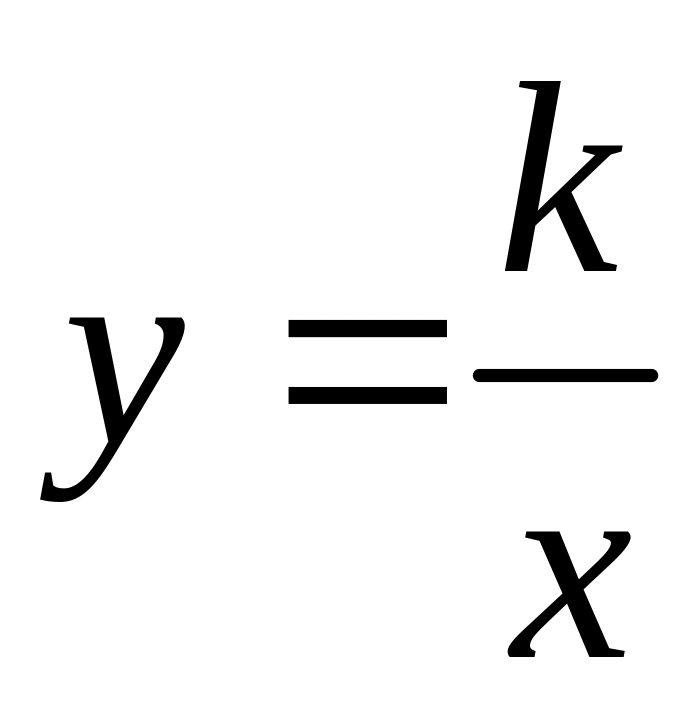 .
Графиком является гипербола.
.
Графиком является гипербола.
При
гипербола расположена в
![]() и
и
![]() четверти, при
- во
четверти, при
- во
![]() и
и
![]() .
.
Дробно-линейная функция
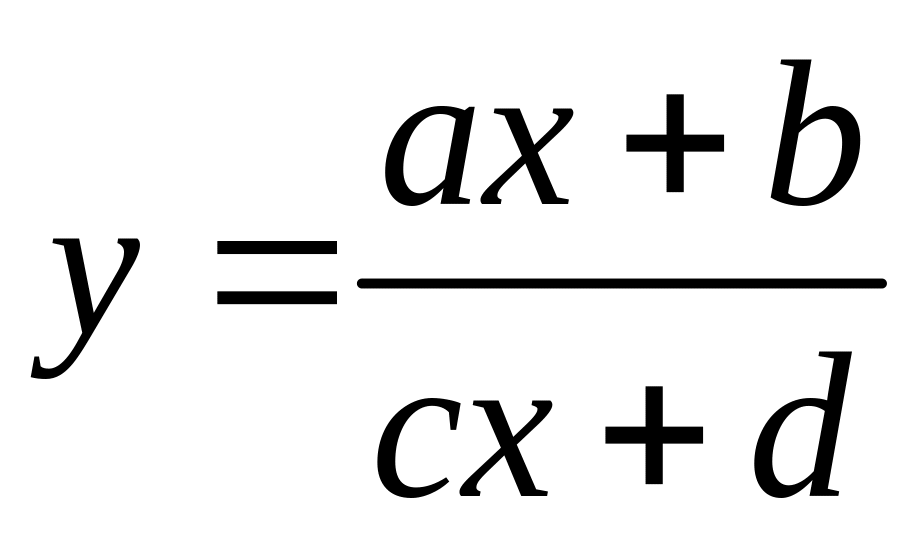 ,
,
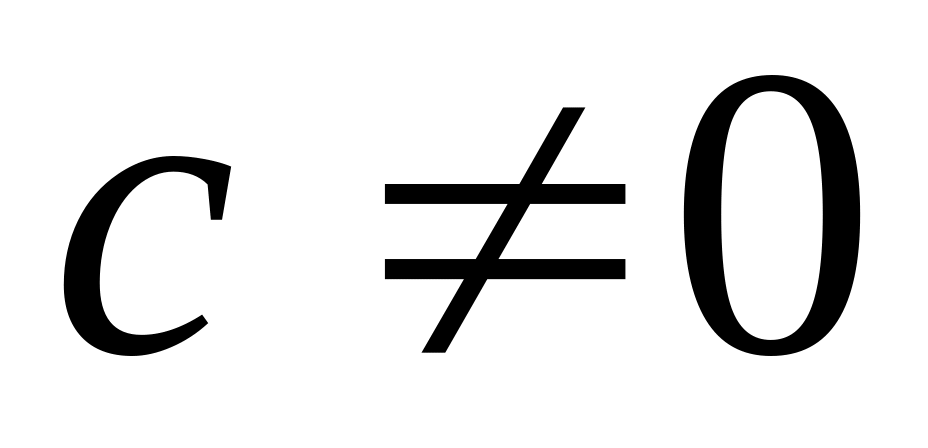 .
Графиком является гипербола
.
Графиком является гипербола
с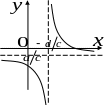 вертикальной асимптотой
вертикальной асимптотой
![]()
и горизонтальной
![]() .
.
Степенная функция
 .
При
графиком является прямая, при
.
При
графиком является прямая, при
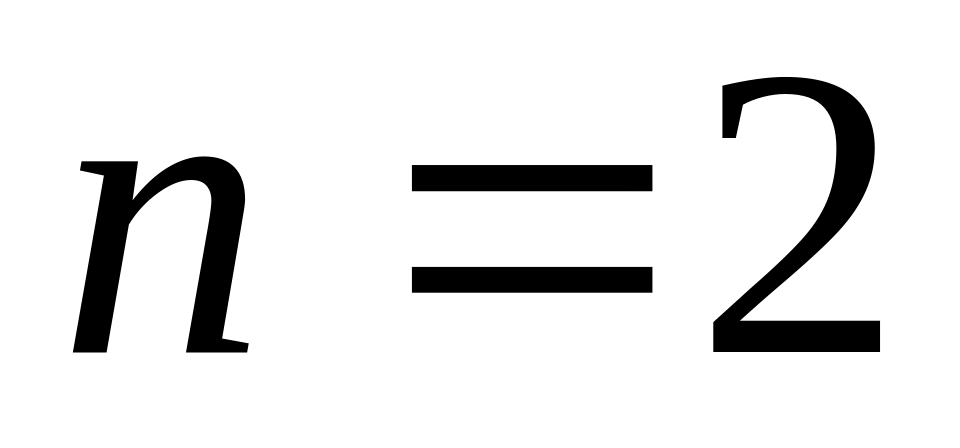 - парабола, при
- парабола, при
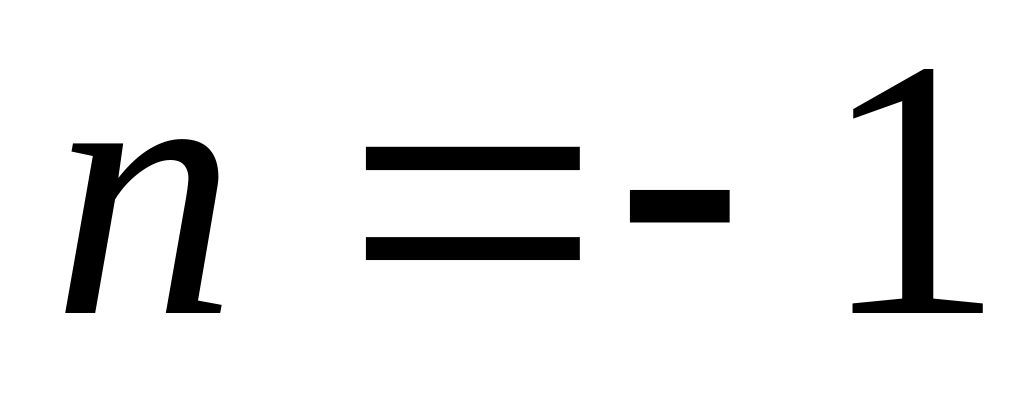 - гипербола. При
- гипербола. При
 графиком функции
графиком функции
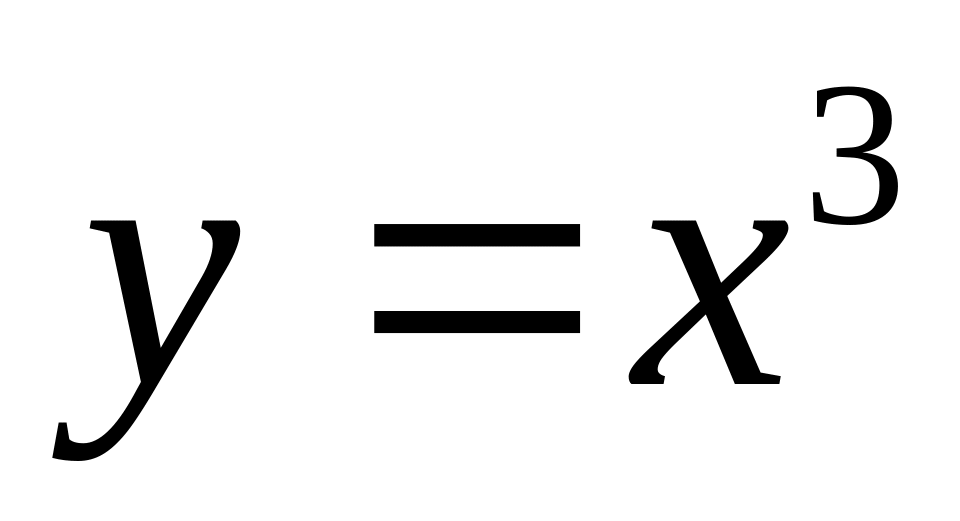 является кубическая парабола.
является кубическая парабола.
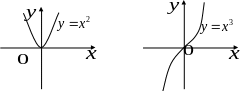
Показательная функция , , .
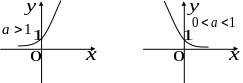
Логарифмическая функция , , .
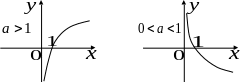
Тригонометрические функции.
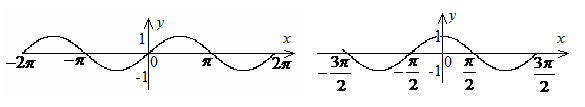
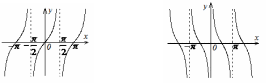
Обратные тригонометрические функции.
![]()
![]()
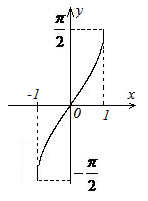
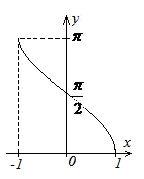
![]()
![]()
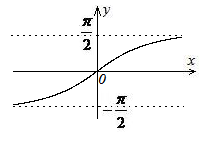
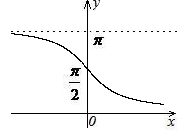
§ 16. Факториал и его свойства.
Определение. Факториалом натурального числа
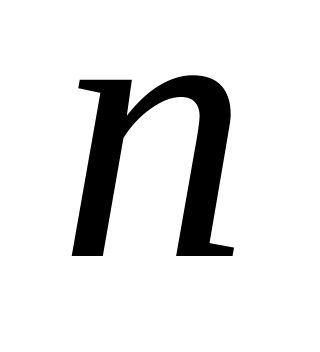 называется произведение всех натуральных
чисел от
до
включительно:
называется произведение всех натуральных
чисел от
до
включительно:
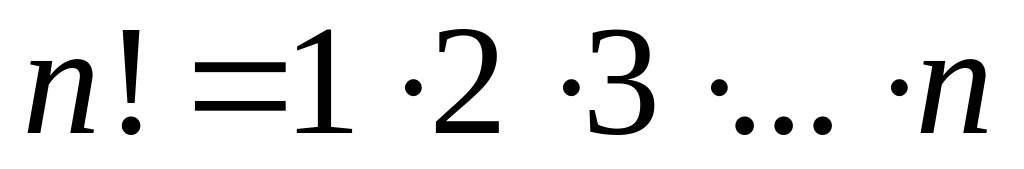 .
При этом
.
При этом
 ,
,
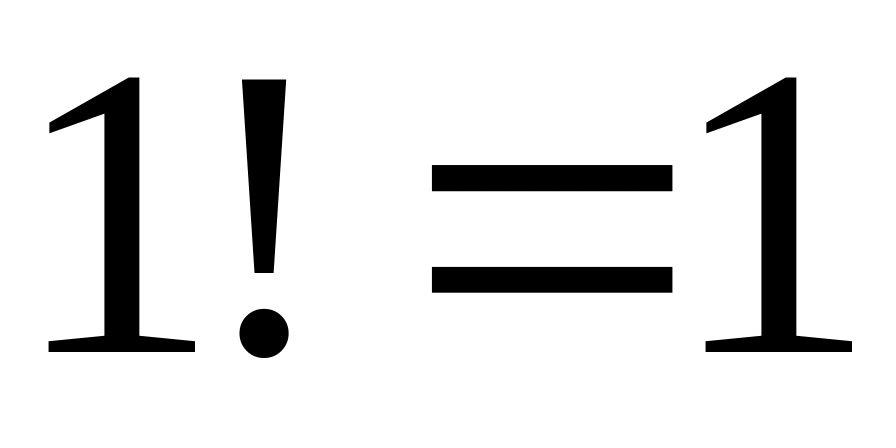 ,
,
 ,
,
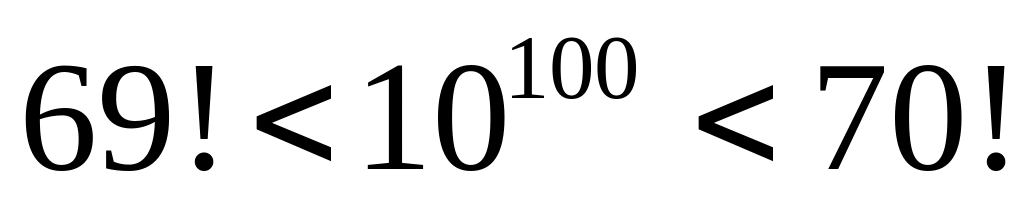 .
.Основное свойство:
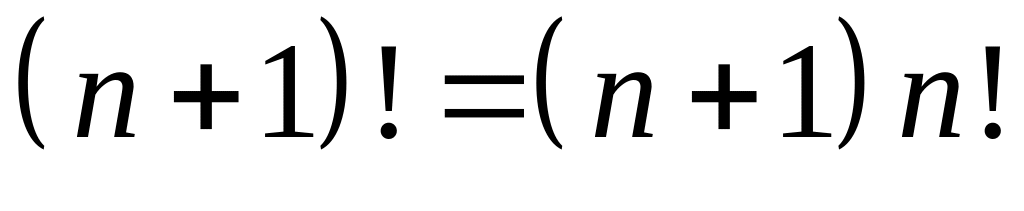 или
или
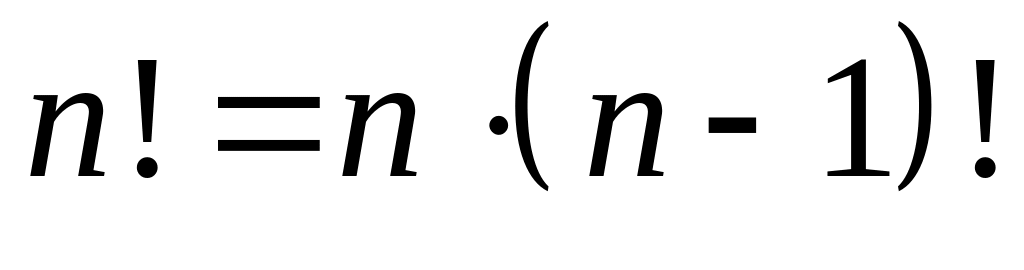
Формулы Стирлинга (для вычисления факториалов больших чисел):
 ,
,
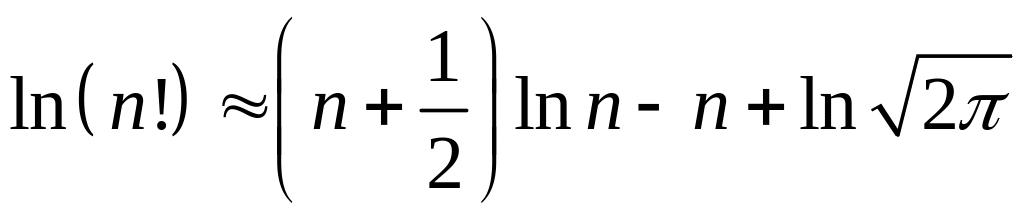 .
.Выражение
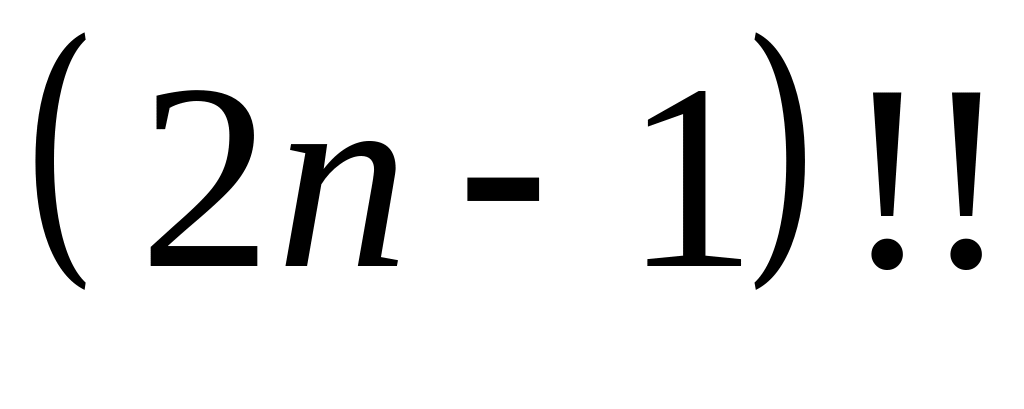 обозначает произведение всех нечётных
натуральных чисел от 1 до
обозначает произведение всех нечётных
натуральных чисел от 1 до
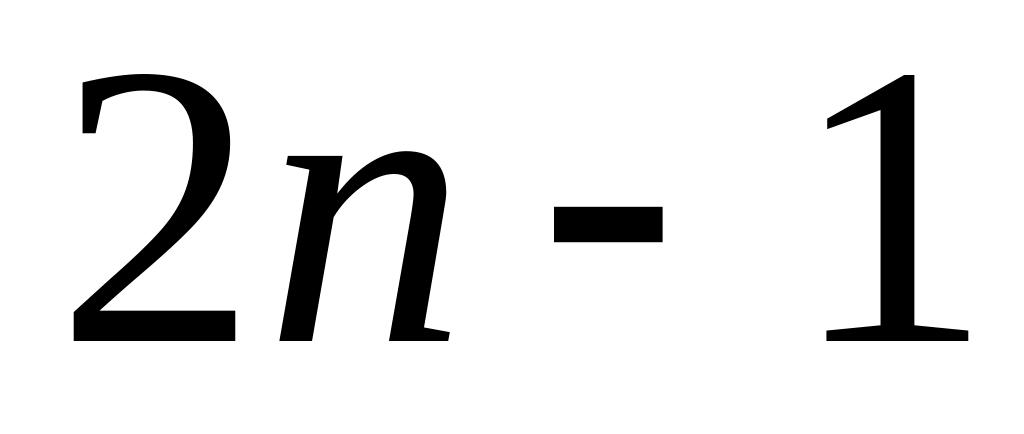 включительно:
включительно:
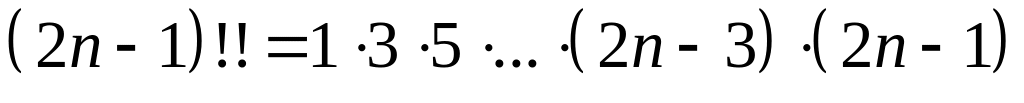 .
.Выражение
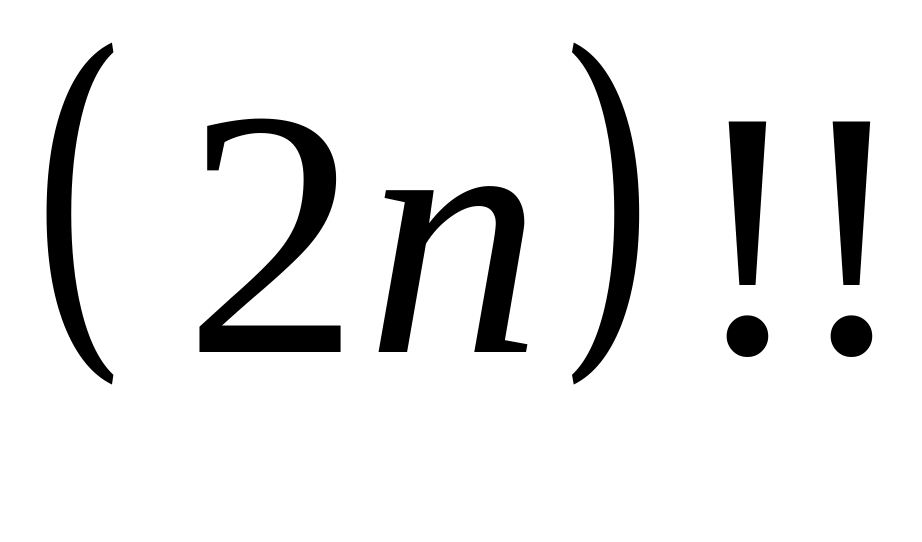 обозначает произведение всех чётных
натуральных чисел
обозначает произведение всех чётных
натуральных чисел
от 2 до
![]() включительно:
включительно:
![]() .
.
§ 17. Основные математические постоянные.
Отношение длины окружности к диаметру
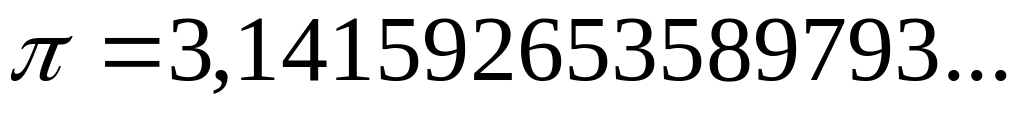
![]() .
.
Основание натурального логарифма (экспонента)
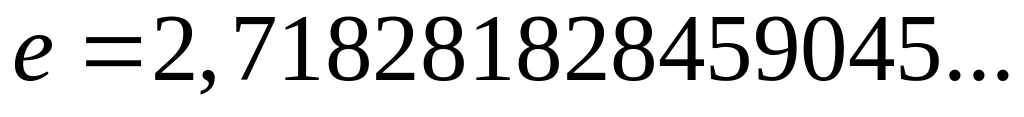
![]() .
.
Золотое сечение. Величина делится на части и
 так, что
так, что
![]() ,
откуда
,
откуда
![]() .
.
§ 18. Конечные числовые суммы.
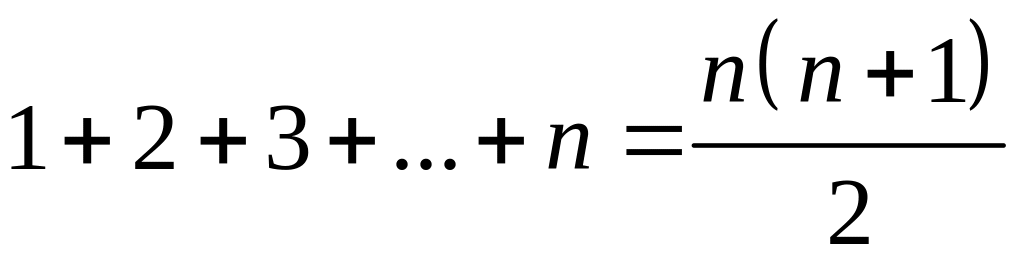 .
.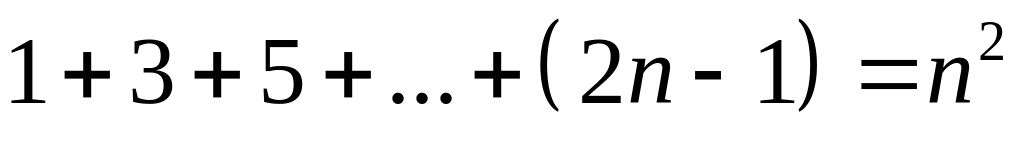 .
.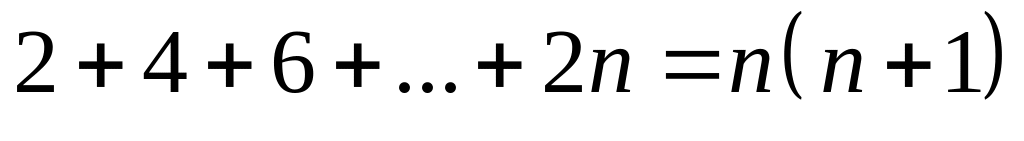 .
.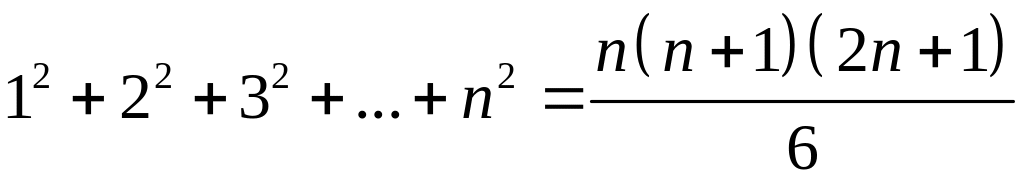 .
.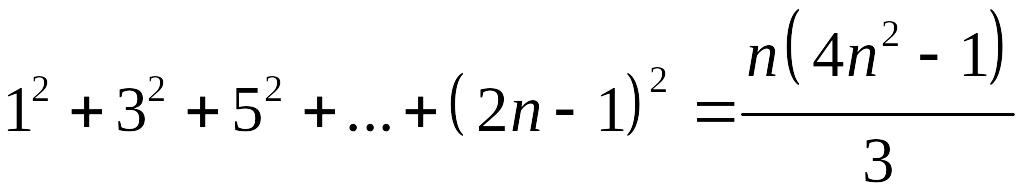 .
.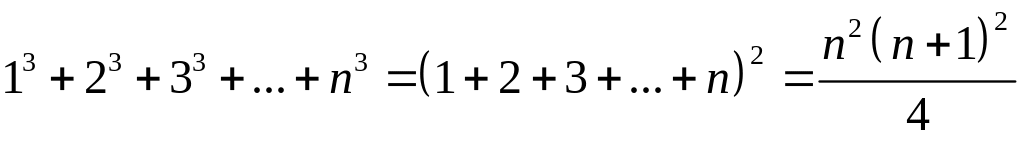 .
.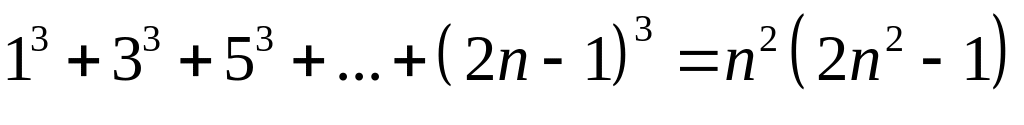 .
.
§ 19. Часто используемые неравенства.
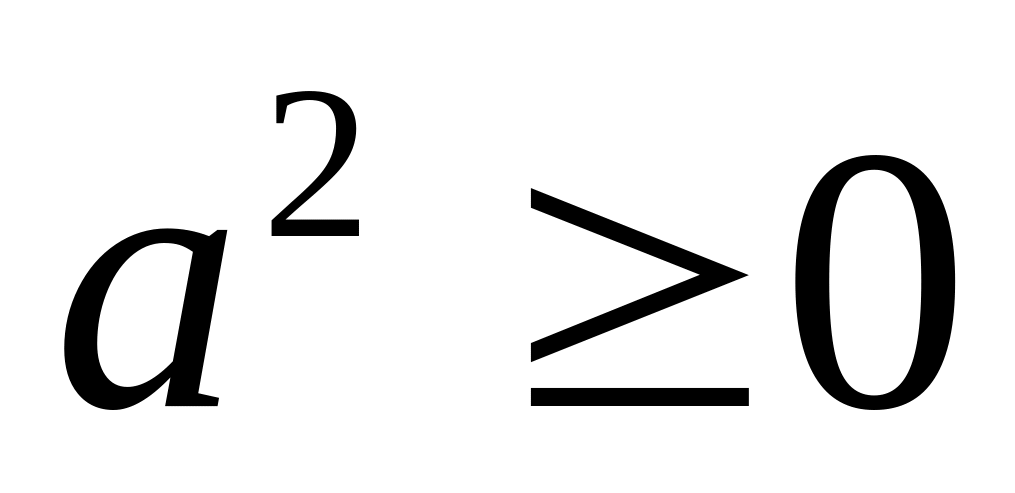 при любом значении
.
при любом значении
.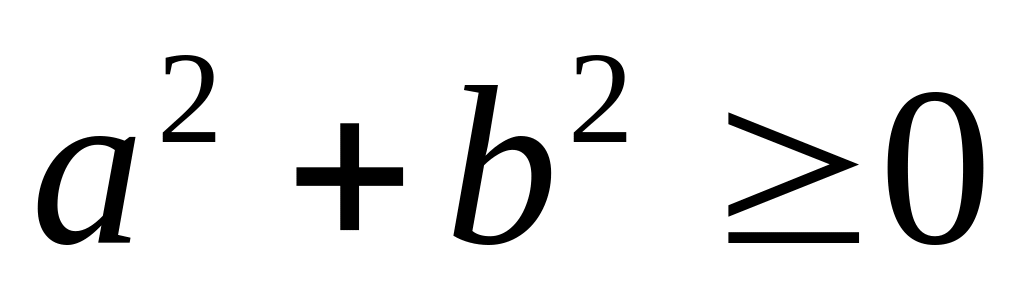 при любых значениях
и
.
при любых значениях
и
.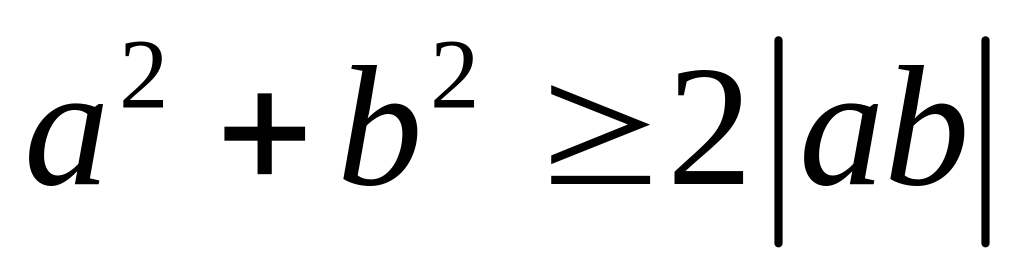 ,
причём равенство достигается при
,
причём равенство достигается при
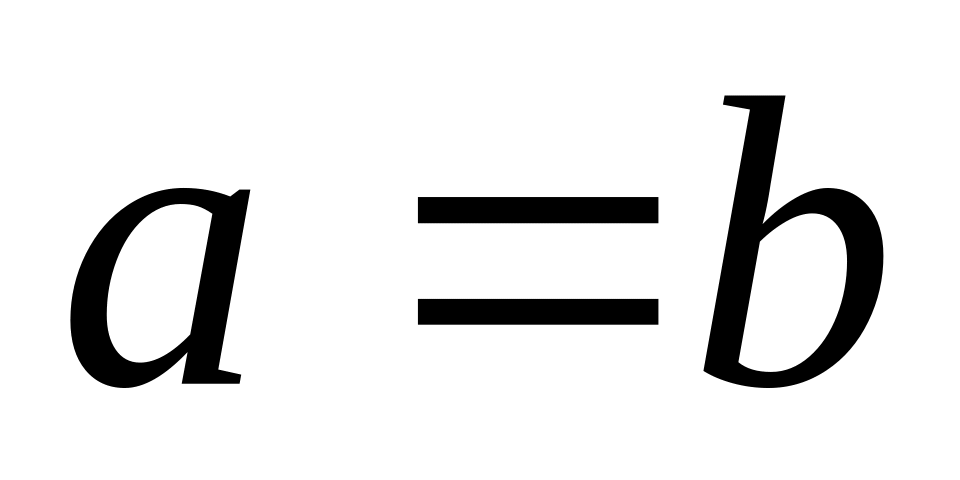 .
.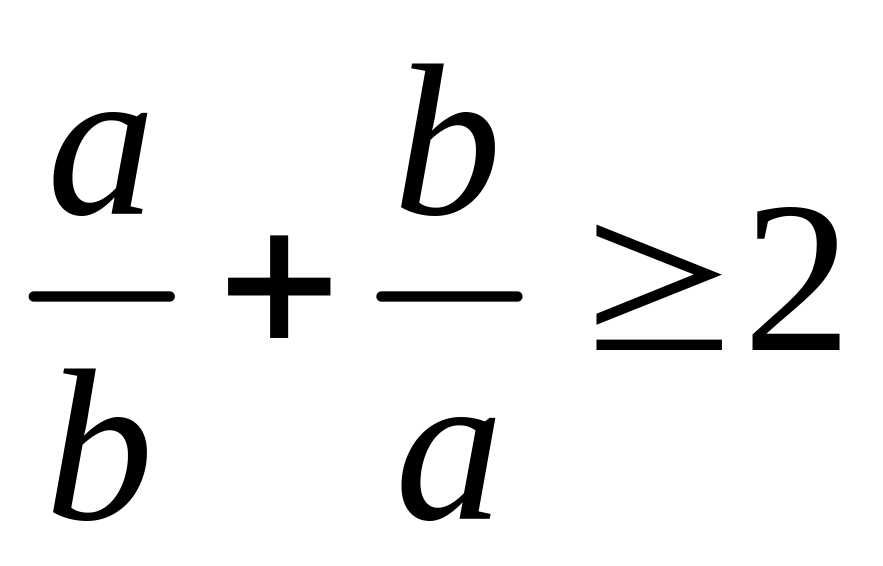 ,
,
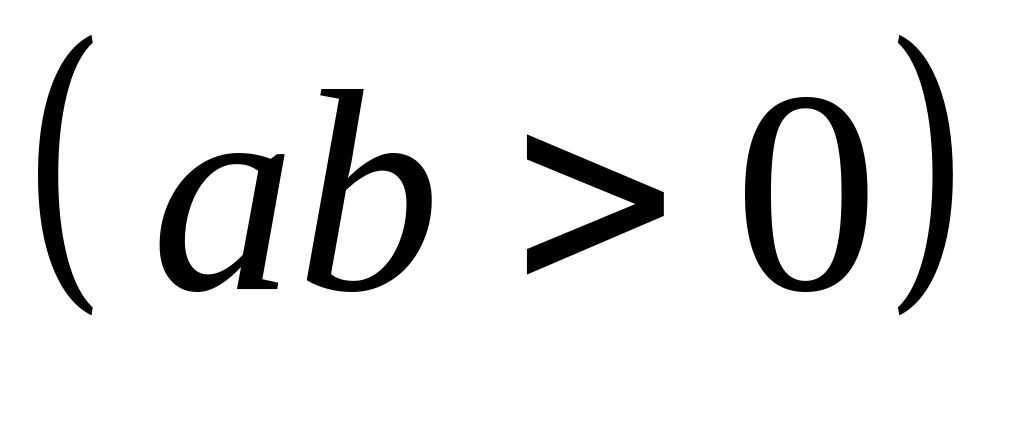 ,
причём равенство достигается при
.
,
причём равенство достигается при
. ,
,
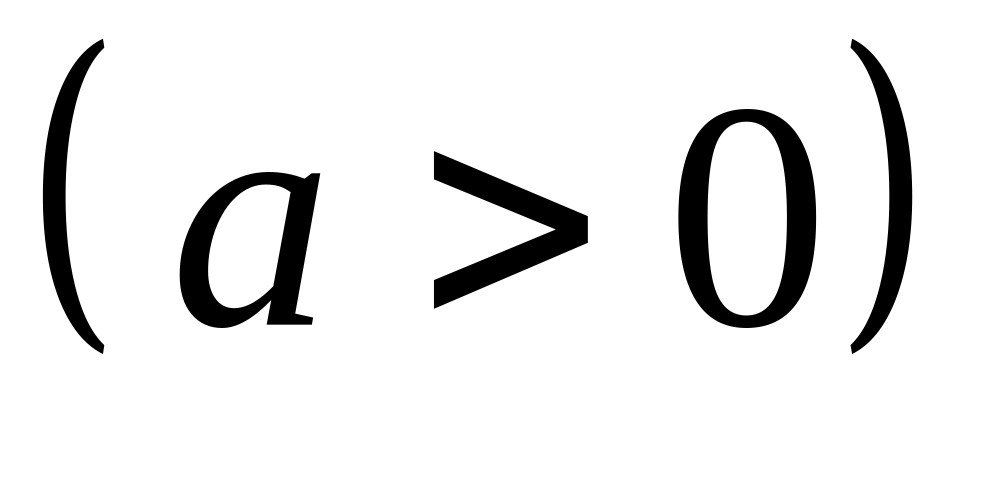 или
или
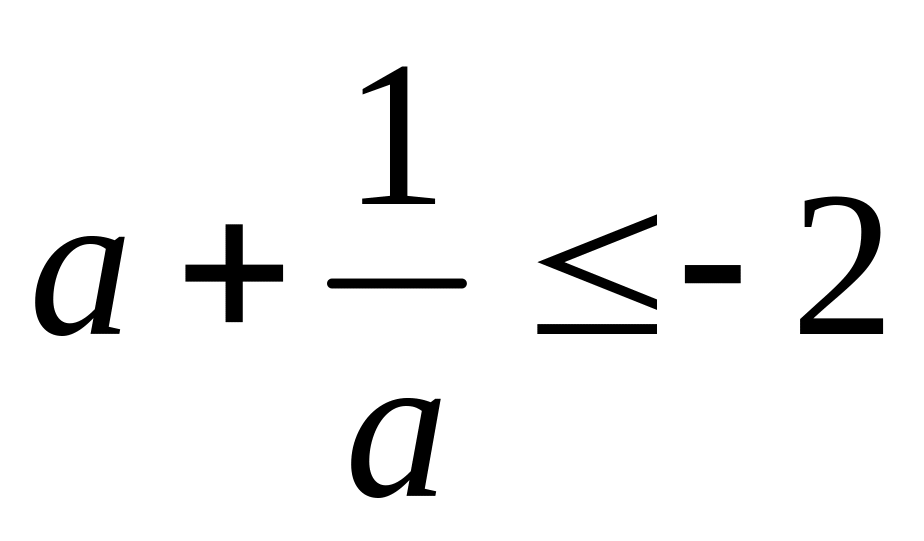 ,
,
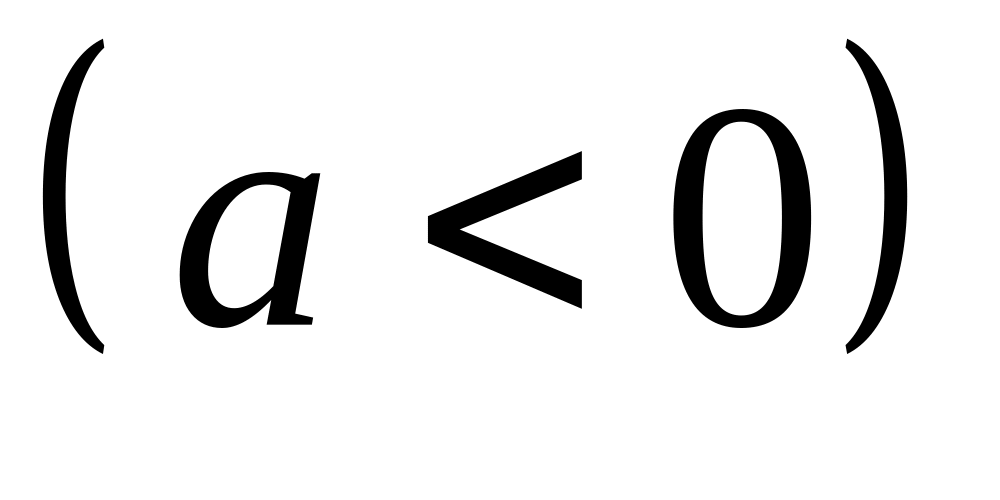 .
.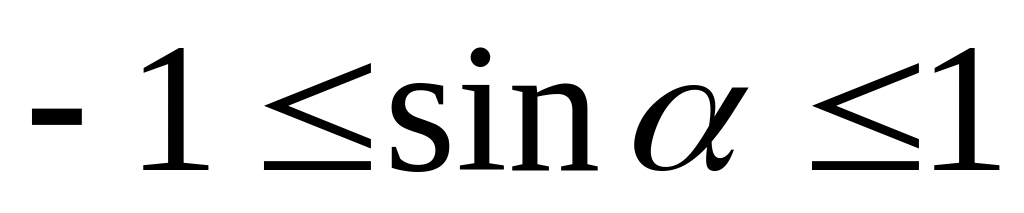 и
и
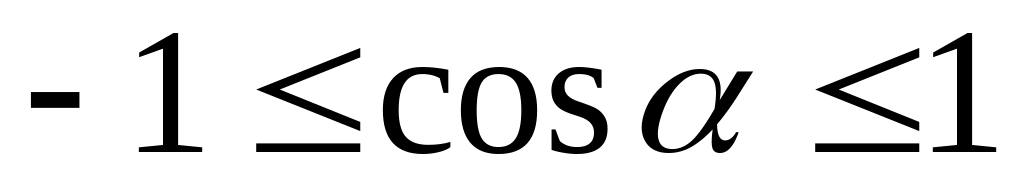 .
.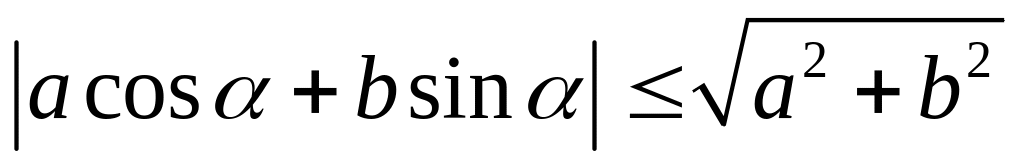 .
.Неравенство Бернулли:
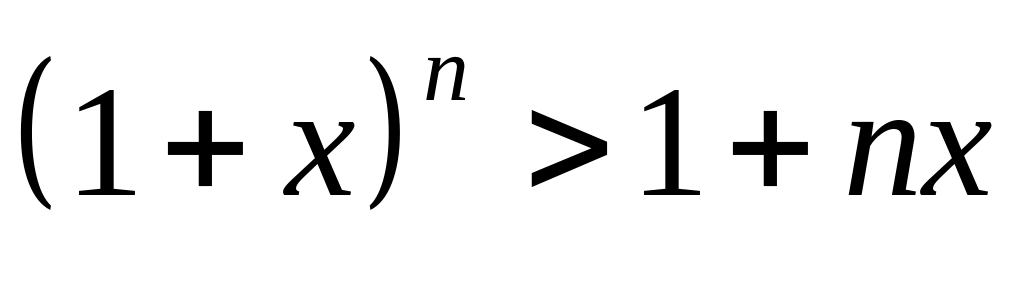 ,
,
.
,
,
.
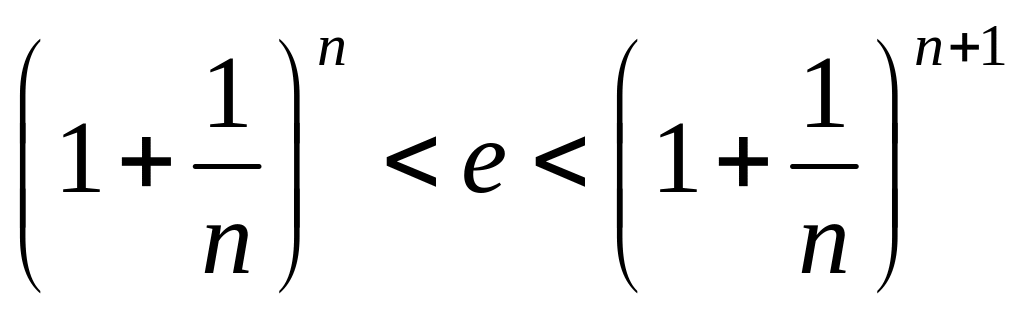 ,
где
.
,
где
. ,
где
.
,
где
.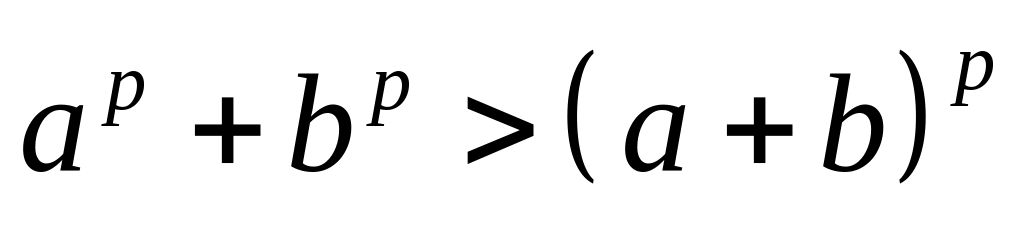 ,
если
,
если
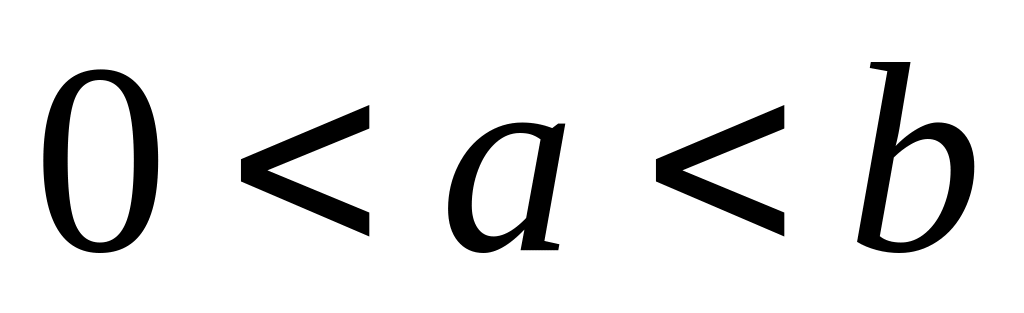 и
и
 .
.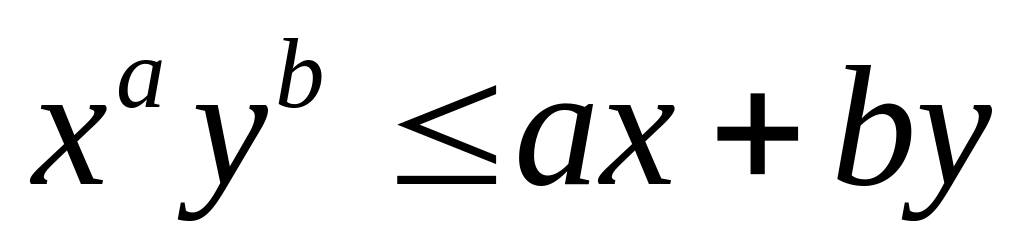 ,
если
,
если
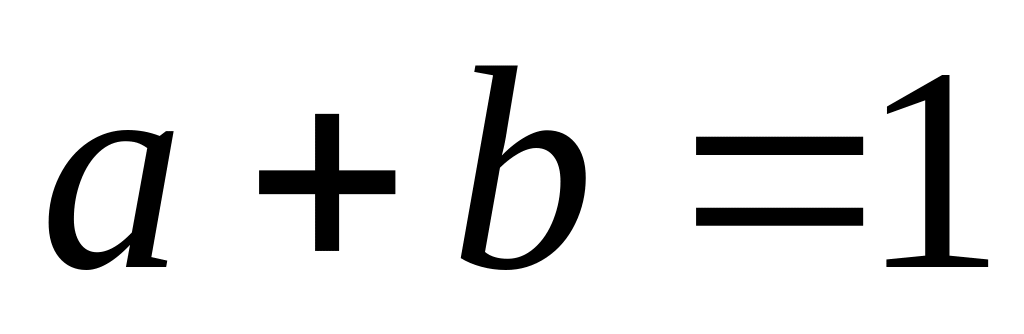 ,
,
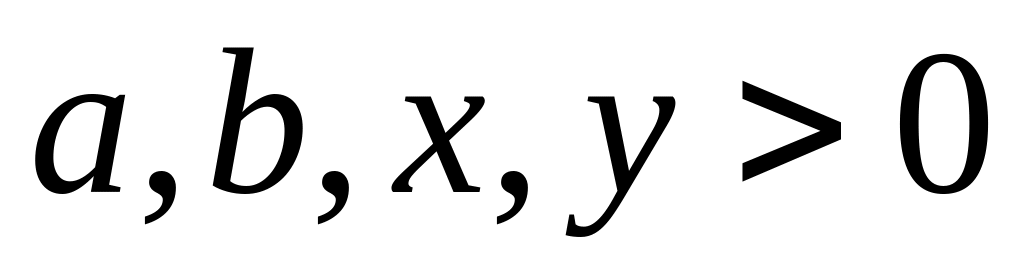 ,
равенство достигается при
,
равенство достигается при
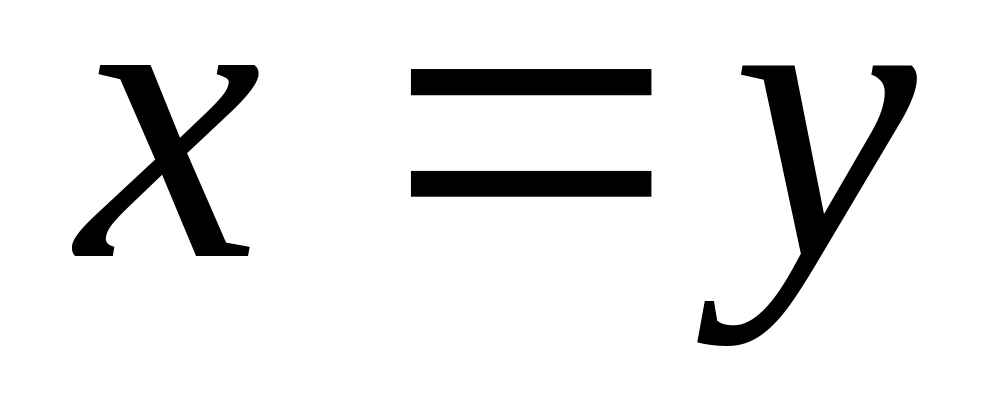 .
.
Библиография
Выгодский М.Я. Справочник по элементарной математике.
Математика в формулах. 5-11 кл.: Справочное пособие. М.: Дрофа, 1998г.
Никольский С.М. и др. Алгебра и начала анализа. Учебники для 10 и 11 класса.
Математика. Подготовка к ЕГЭ-2010. Вступительные испытания. Под редакцией Лысенко Ф.Ф. Ростов-на-Дону, 2009г.
Письменный Д.Т. Готовимся к экзамену по математике. Москва, 2003г.
Ткачук В.В. Математика абитуриенту. Москва, 2006г.
Сборник задач по математике для поступающих в вузы. Под редакцией
Сканави М.И. Москва, 2006г.
В авторской редакции.
Компьютерная вёрстка Шубовича А.А.
Подписано в печать Формат
![]()
Усл. печ. л. 1,17 Тираж 100. Заказ
Издательско-полиграфический комплекс ВГСХА «Нива»
