
- •Часть I
- •§ 1. Тригонометрия.
- •Радианная мера угла.
- •Тригонометрические величины некоторых углов.
- •Выражение одних тригонометрических функций через другие.
- •Формулы приведения.
- •Значения обратных тригонометрических функций некоторых углов.
- •Формулы решения простейших тригонометрических уравнений.
- •Частные случаи простейших тригонометрических уравнений.
- •§ 2. Таблица квадратов натуральных чисел от 10 до 99.
- •§ 3. Формулы преобразования многочленов.
- •Формулы сокращённого умножения.
- •Следствия из формул сокращённого умножения.
- •§ 4. Средние величины.
- •Неравенства между средними величинами:
- •§ 5. Модуль и его свойства.
- •§ 6. Степени и корни.
- •§ 7. Арифметическая прогрессия.
- •§ 8. Геометрическая прогрессия.
- •§ 9. Область определения функции.
- •§ 10. Множество значений функции.
- •§ 11. Чётность, нечётность, периодичность функции.
- •§ 12. Производная функции.
- •§ 13. Первообразная функции.
- •§ 14. Показательная функция.
- •§ 15. Логарифмы и логарифмическая функция.
- •§ 17. Графики элементарных функций.
- •§ 16. Факториал и его свойства.
- •§ 17. Основные математические постоянные.
- •§ 18. Конечные числовые суммы.
- •§ 19. Часто используемые неравенства.
- •400002, Волгоград, Университетский пр-т, 26
§ 3. Формулы преобразования многочленов.
Формулы сокращённого умножения.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Следствия из формул сокращённого умножения.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Разложение квадратного трёхчлена на множители.
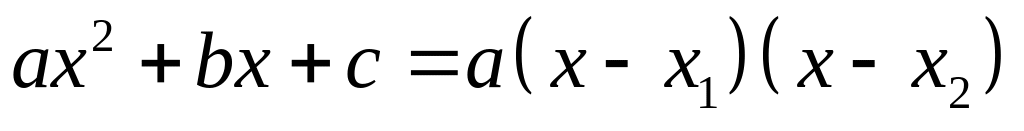 ,
где
,
где
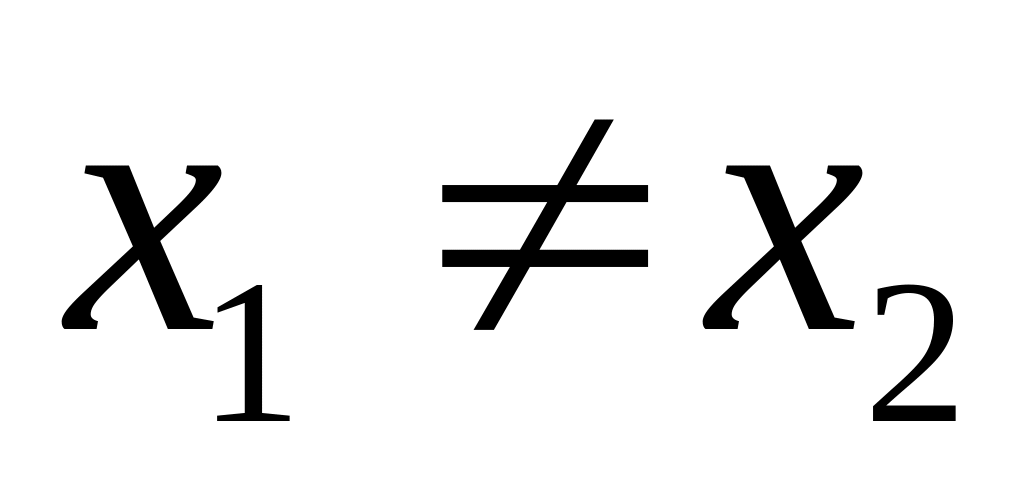 - корни уравнения
- корни уравнения
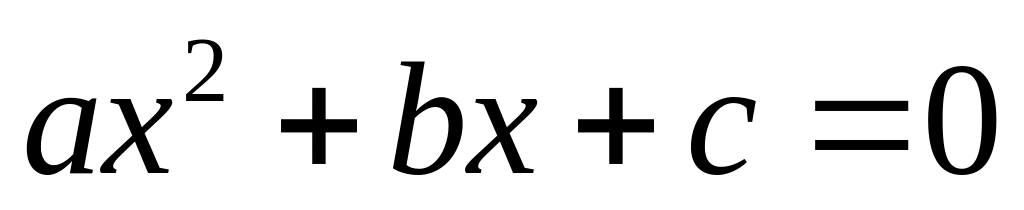 ;
;
![]() ,
где
,
где
![]() ,
,
![]() .
.
§ 4. Средние величины.
Среднее арифметическое
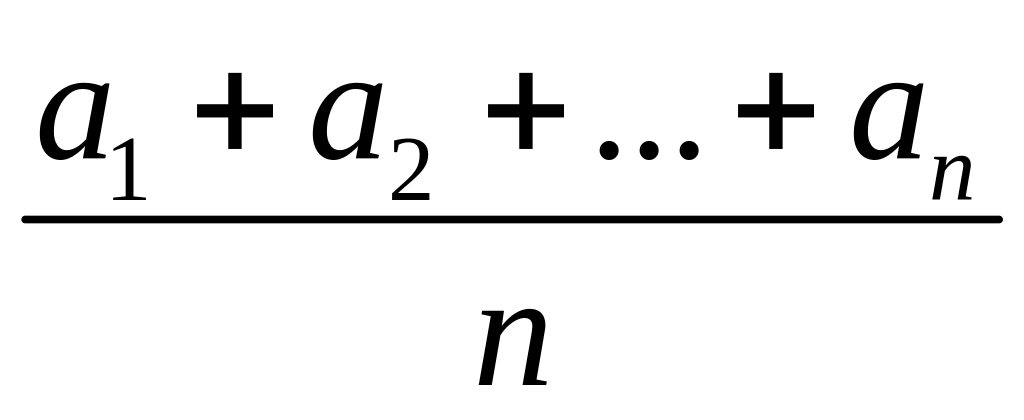 ;
для двух чисел
;
для двух чисел
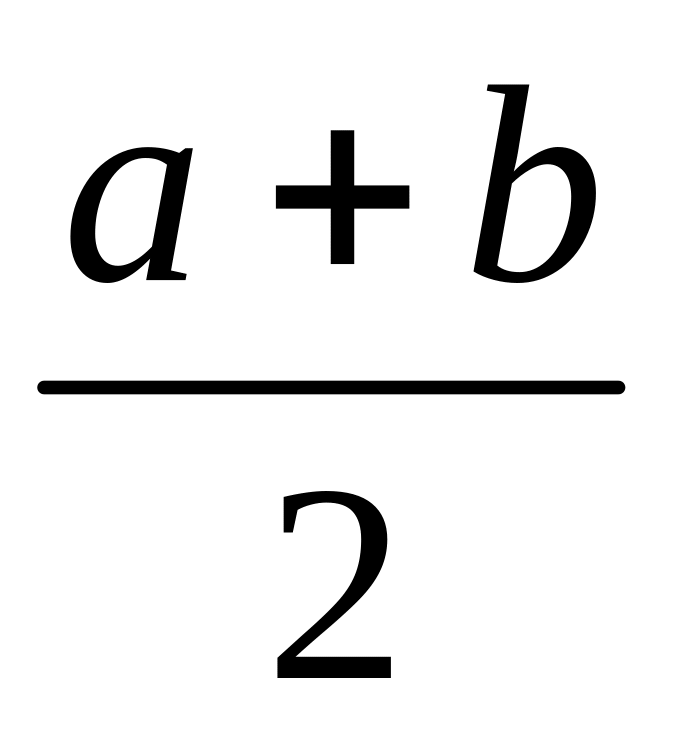 .
.Среднее геометрическое (пропорциональное)
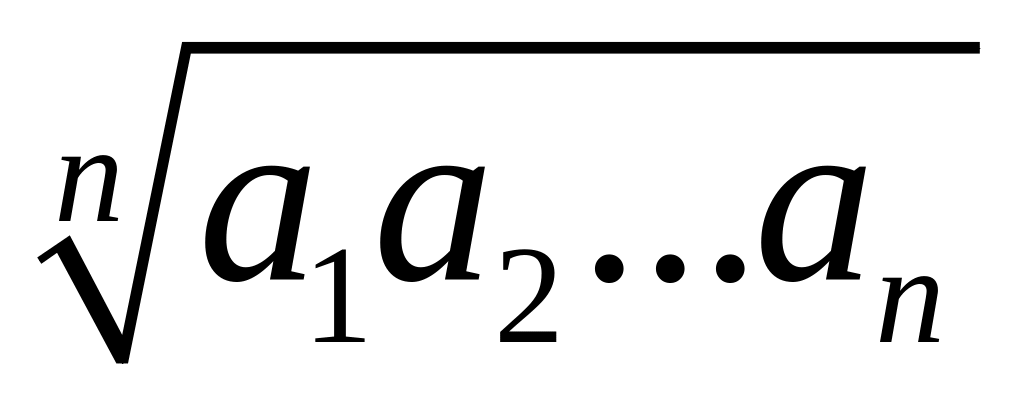 ;
для двух чисел
;
для двух чисел
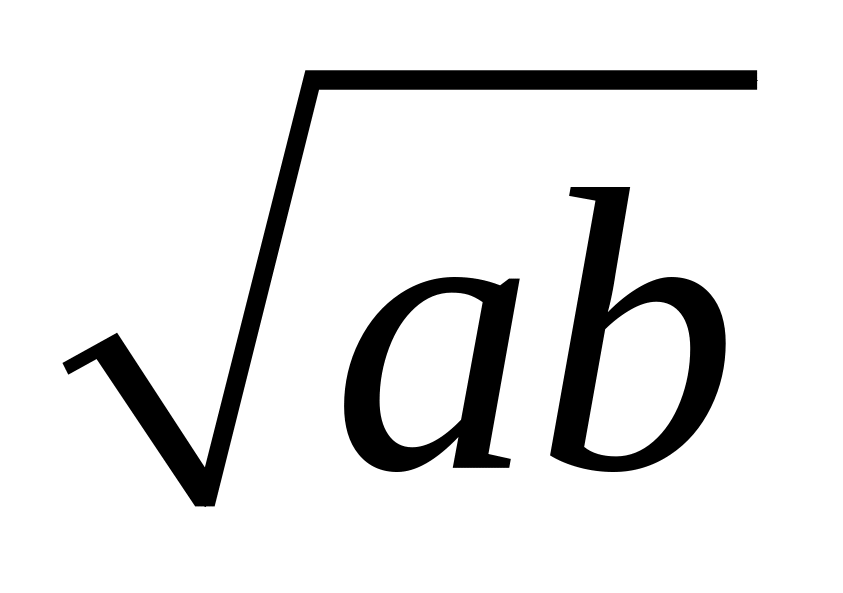 .
.Среднее квадратичное
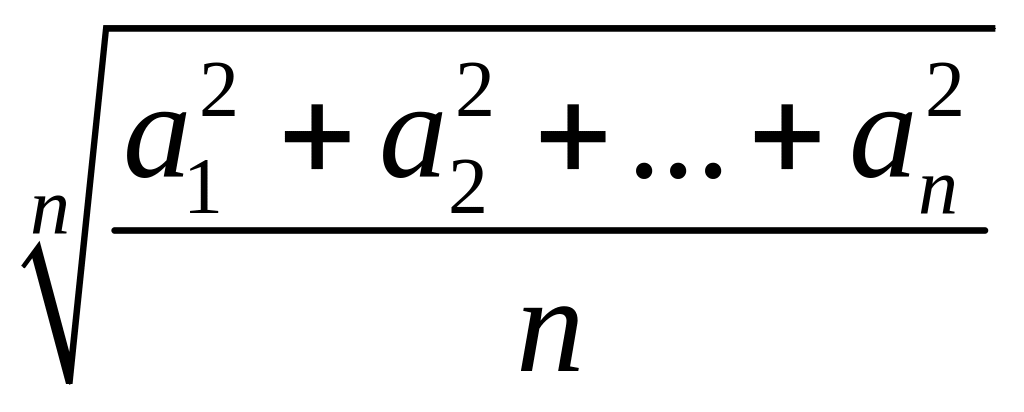 ;
для двух чисел
;
для двух чисел
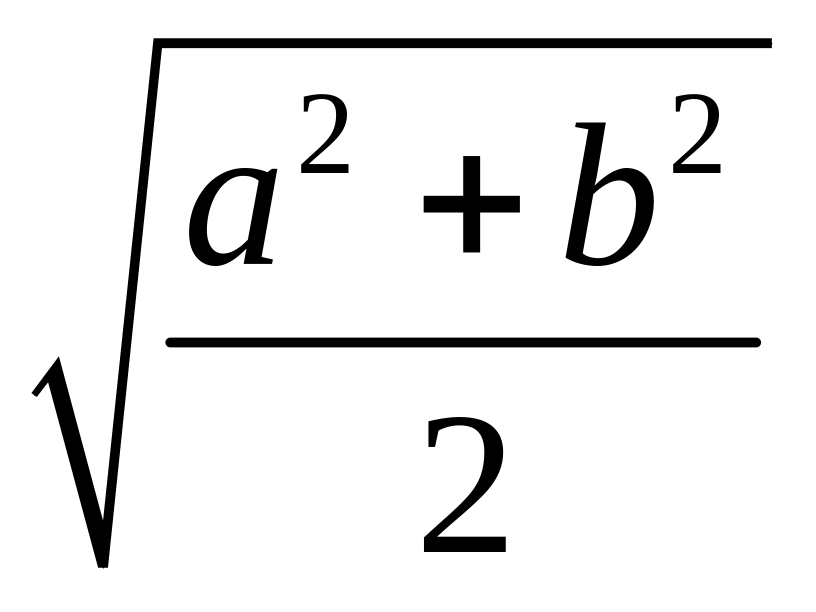 .
.Среднее гармоническое
 ;
для двух чисел
;
для двух чисел
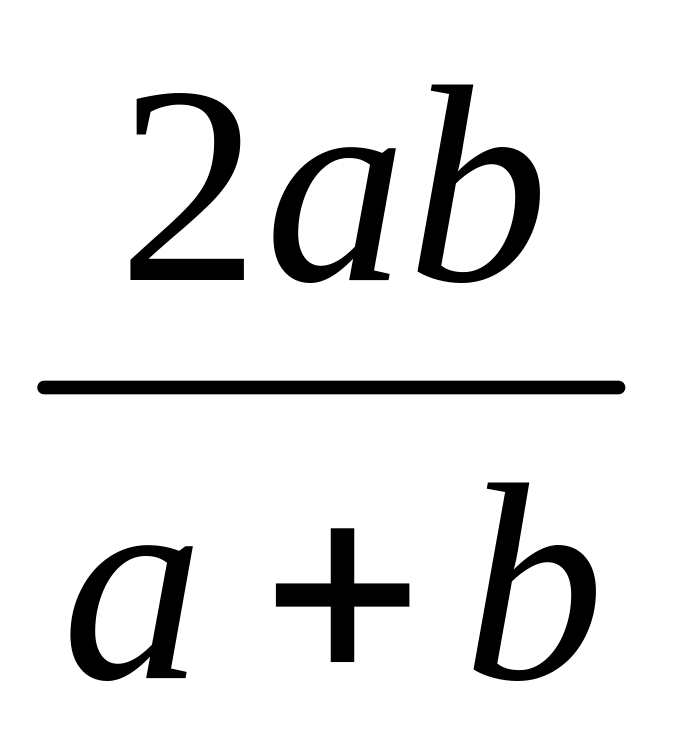 .
.Неравенства между средними величинами:
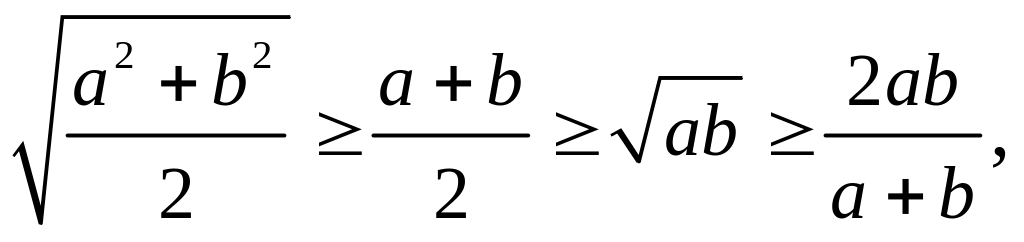
![]() .
.
§ 5. Модуль и его свойства.
По определению,
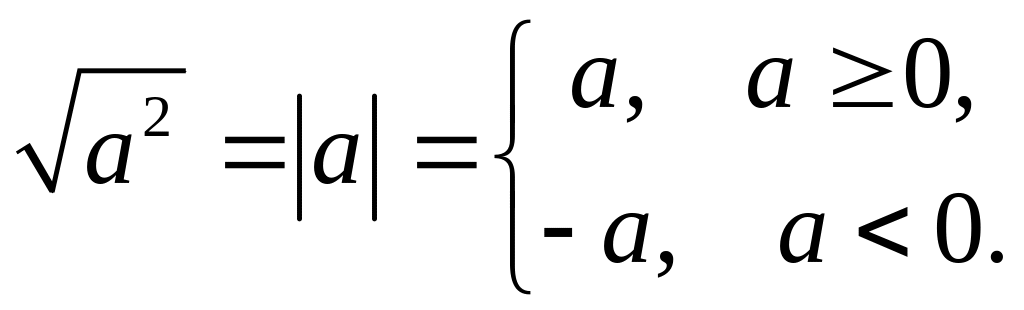 Аналогично,
Аналогично,
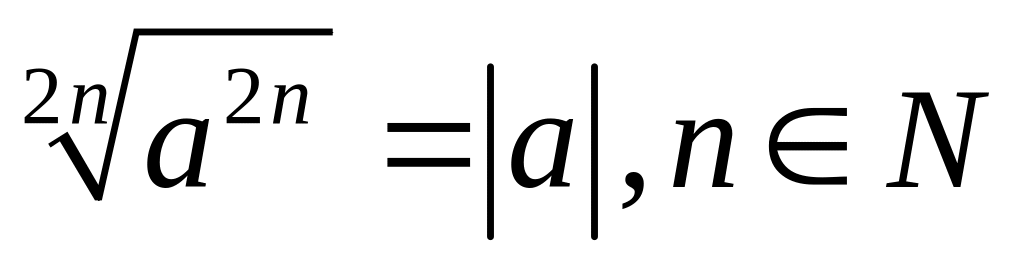 .
.При решении уравнений и неравенств с модулем:
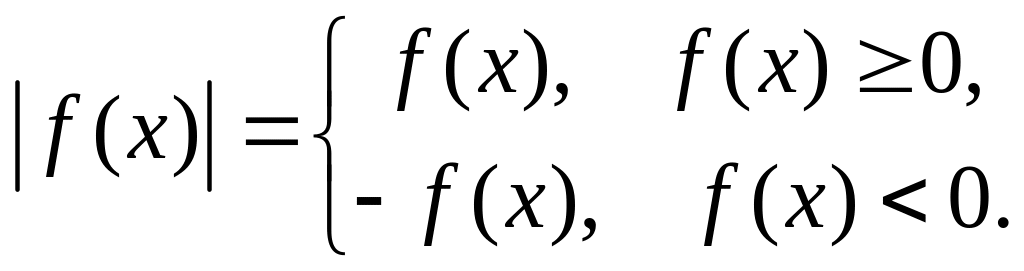
Свойства модуля:
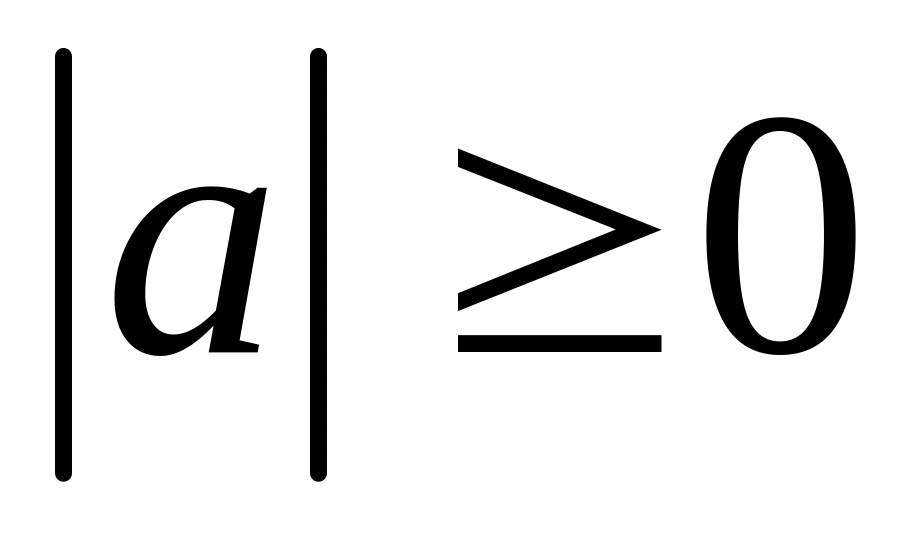 ;
;
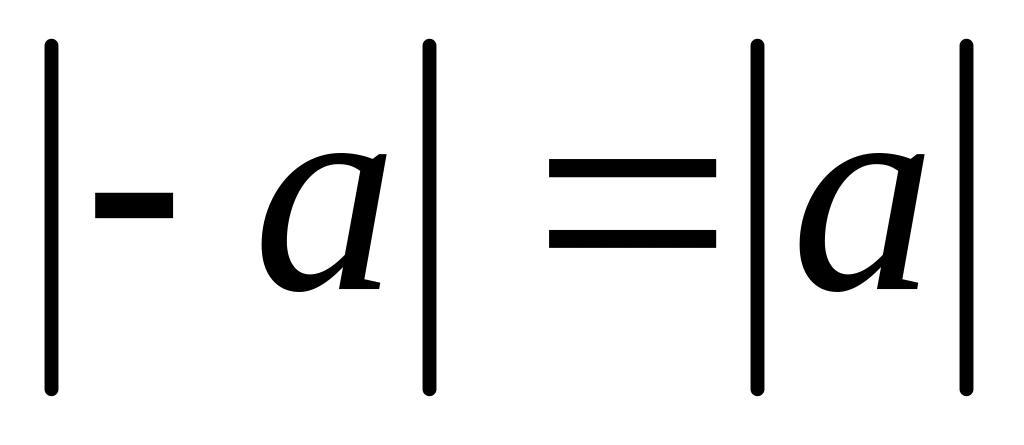 ;
;
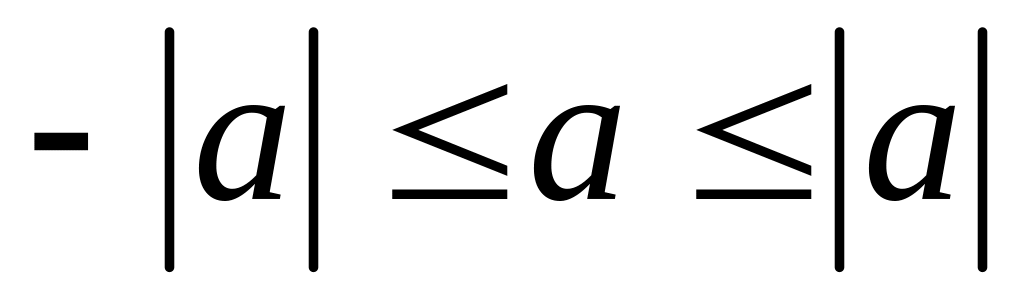 ;
;
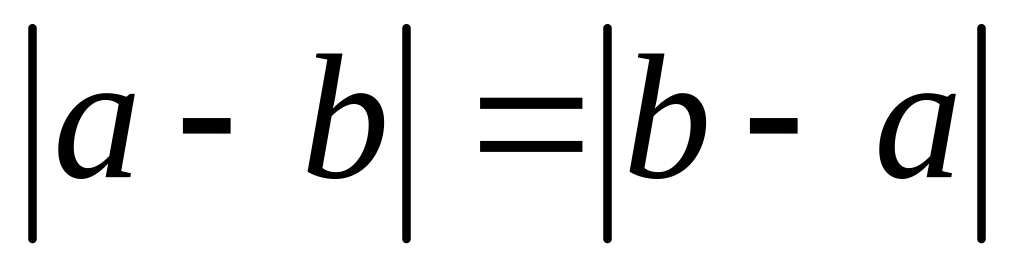 ;
;
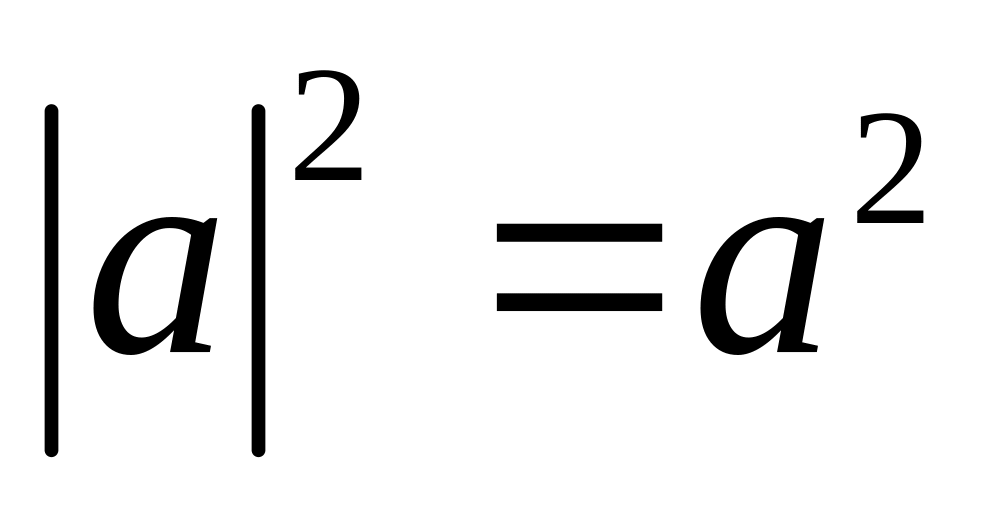 ;
;
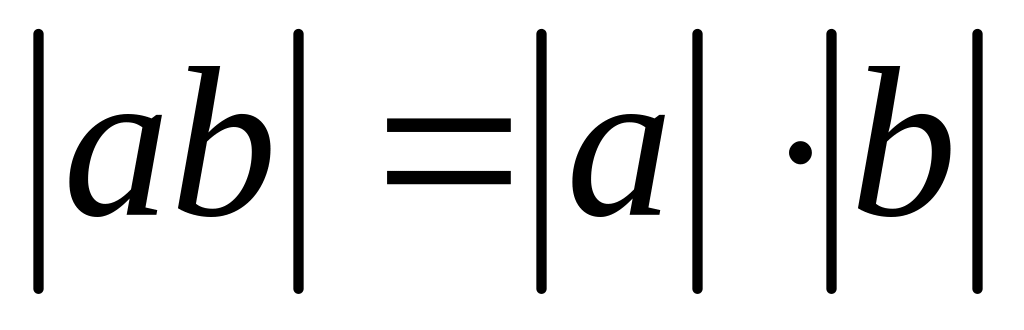 ;
;
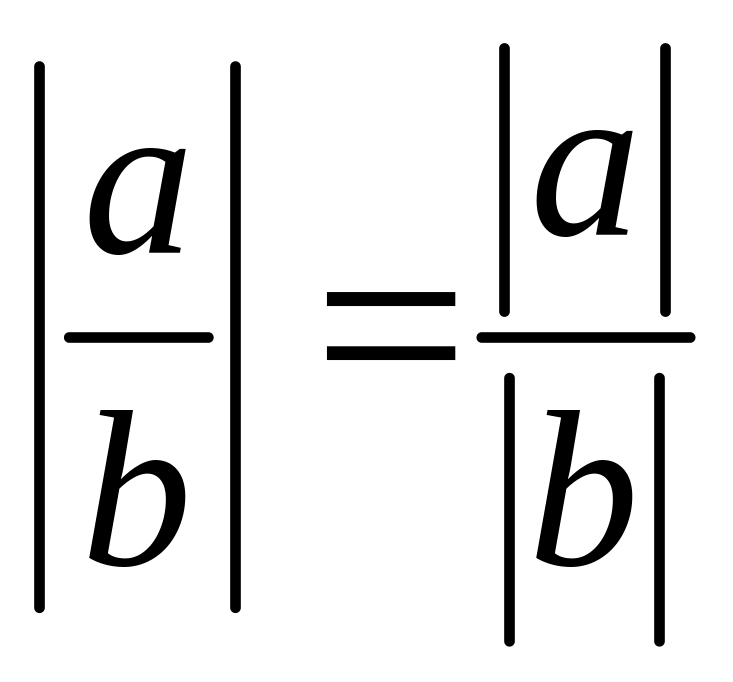 ,
,
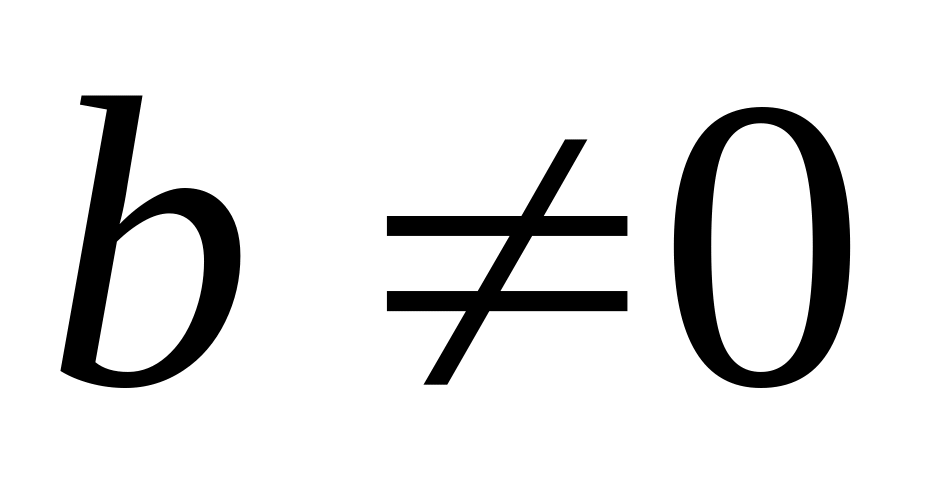 ;
;
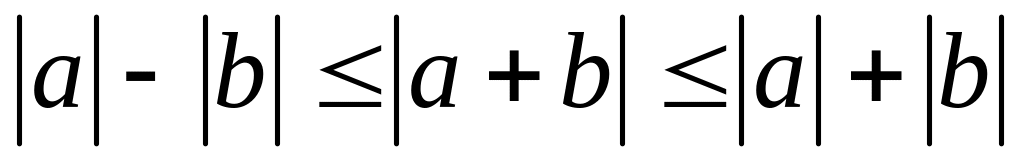 ;
;
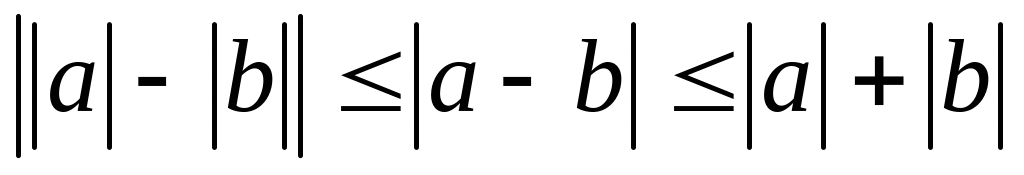 .
.Расстояние между точками
 и
и
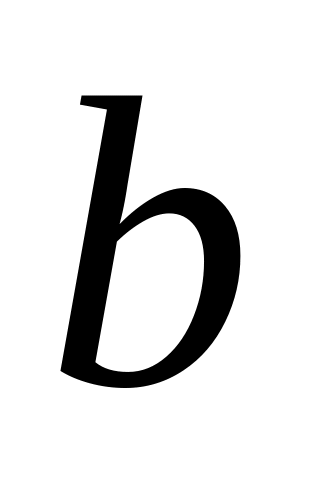 равно
равно
 ;
расстояние между соответствующими
точками графиков функций
;
расстояние между соответствующими
точками графиков функций
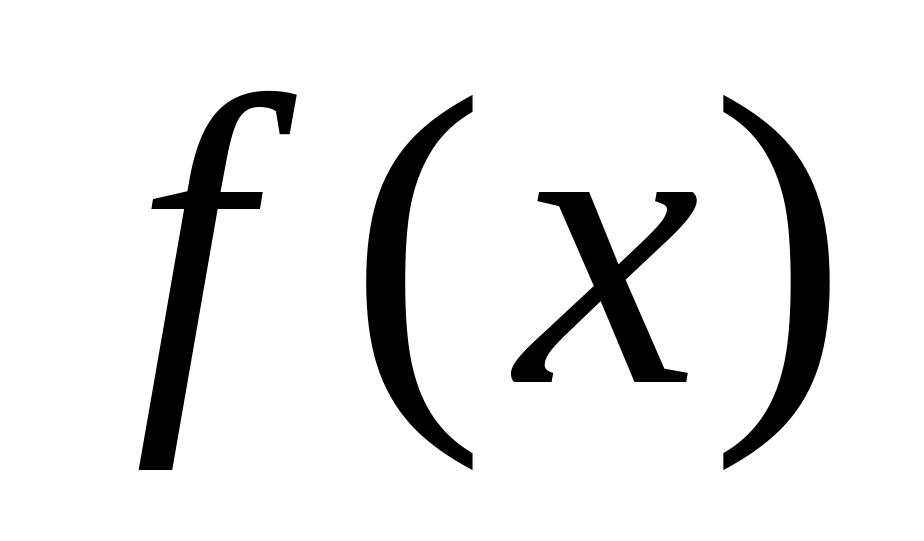 и
и
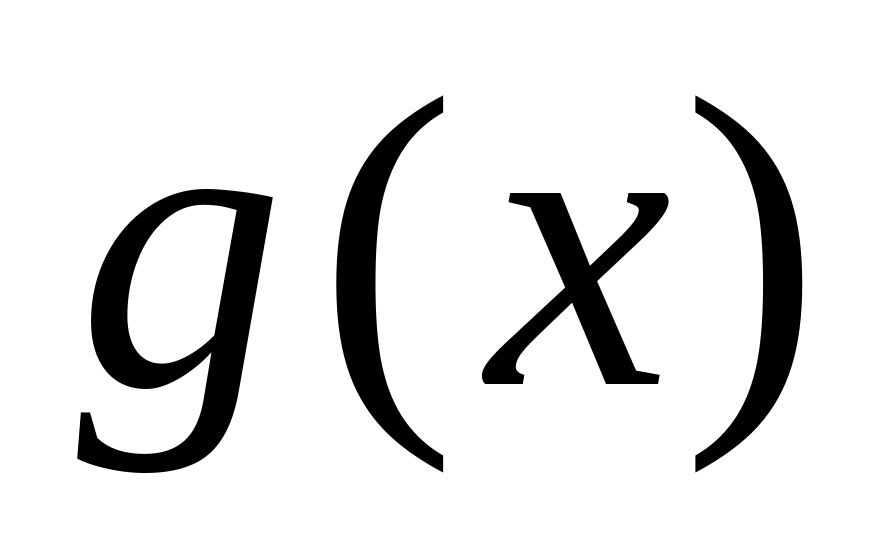 равно
равно
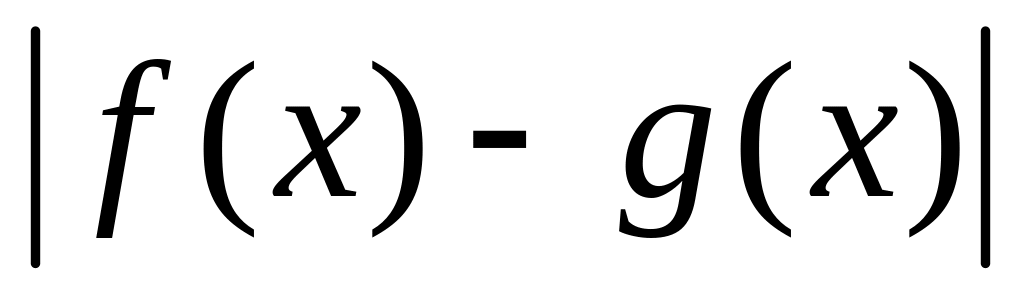 .
.Уравнение с модулем:
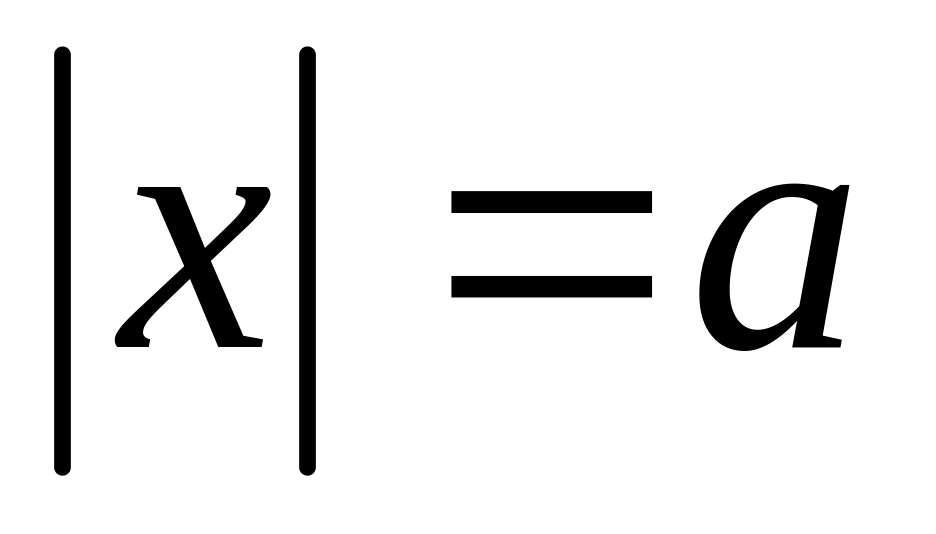 ,
,
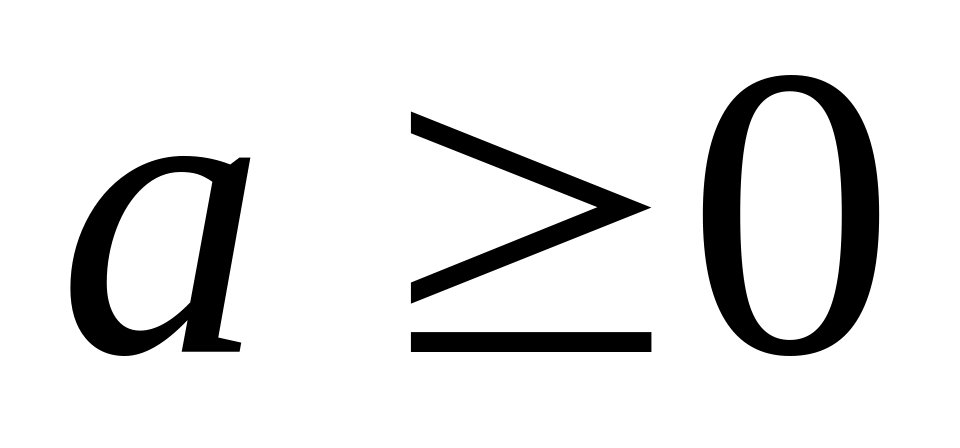
 ;
; .
.Неравенства с модулем:

 (пересечение)
или
(пересечение)
или
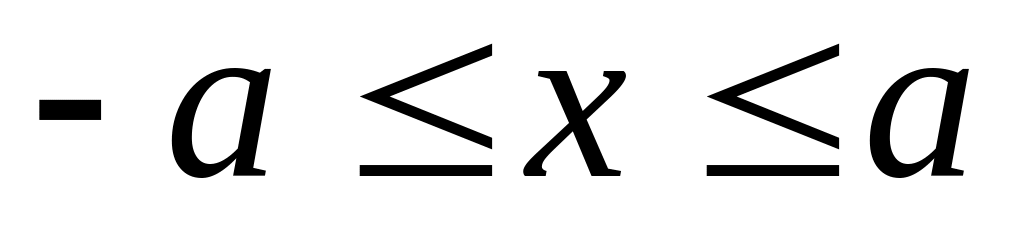 ;
;
![]() ,
,
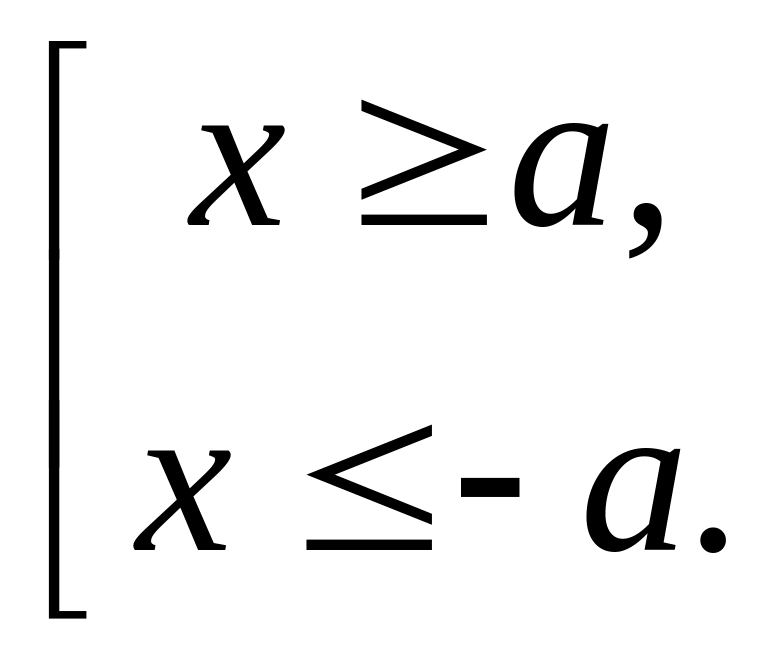 (объединение).
(объединение).
§ 6. Степени и корни.
Определение.
 ,
,
 ;
;
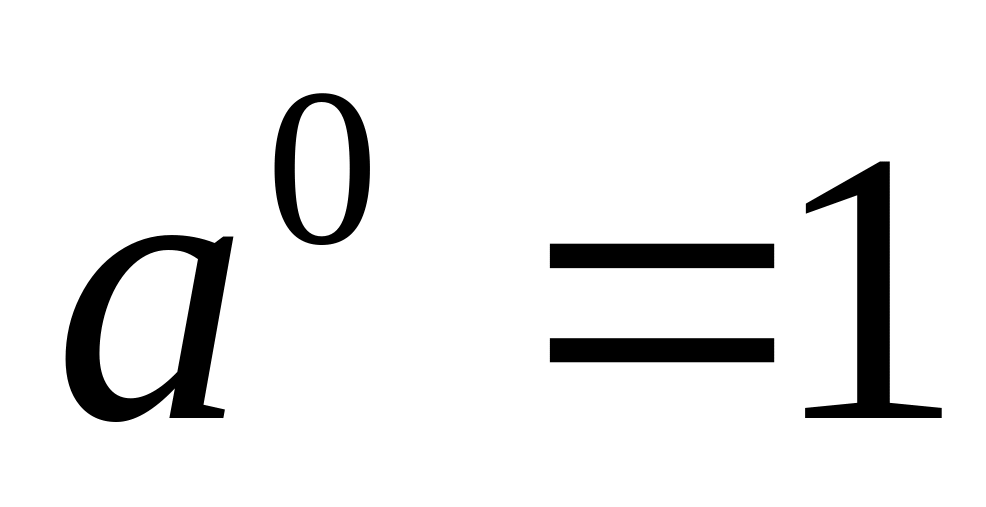 ,
если
,
если
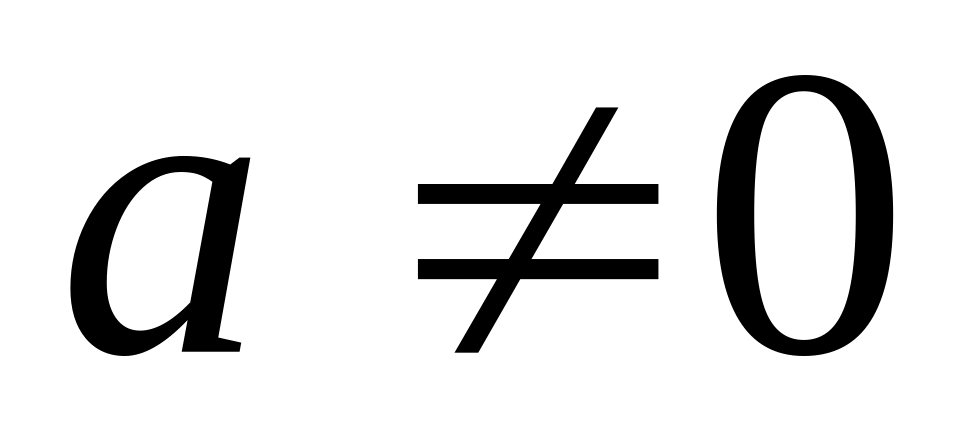 .
.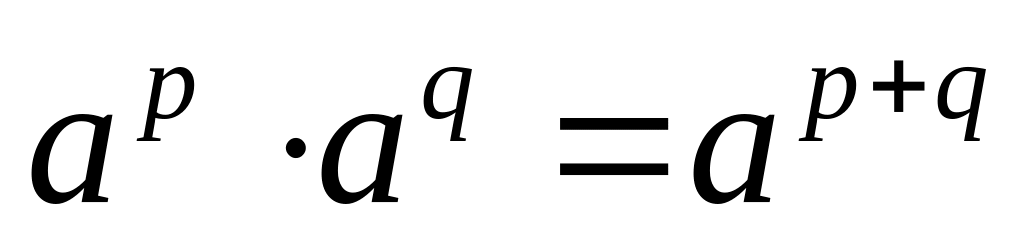 ;
;
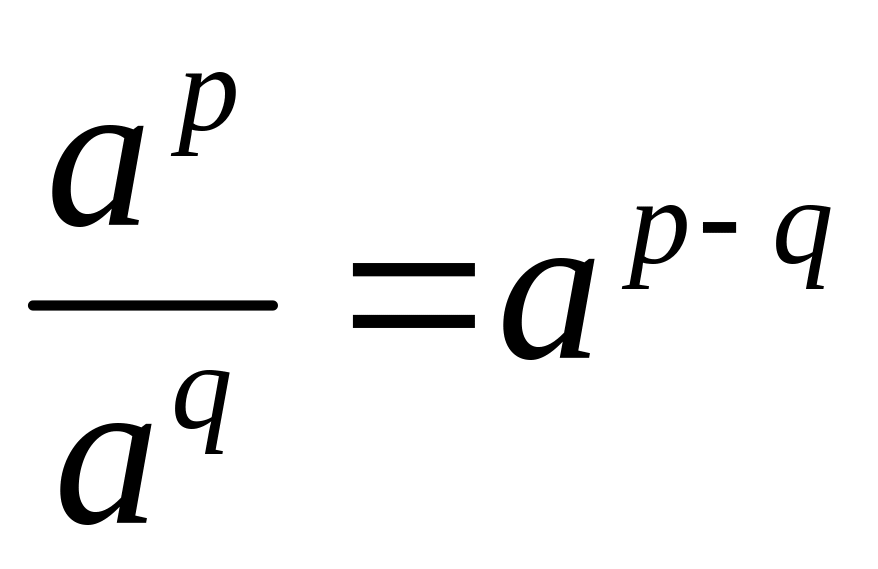 ;
;
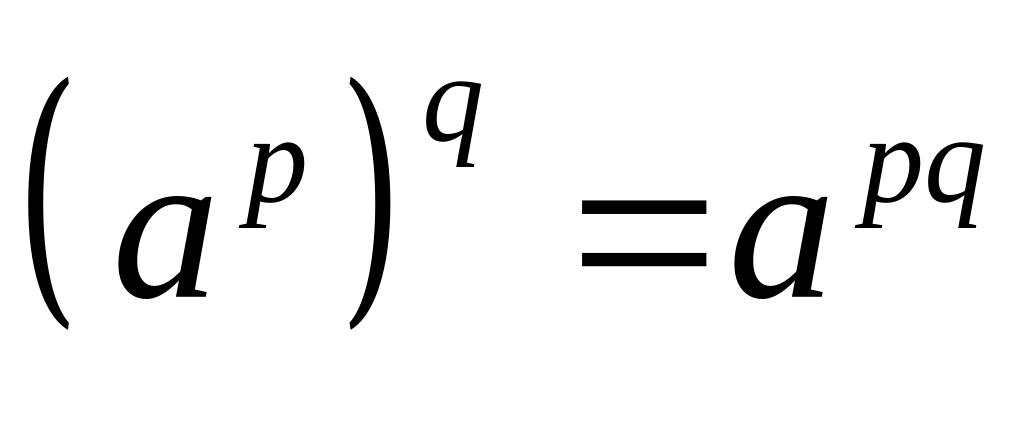 ;
;
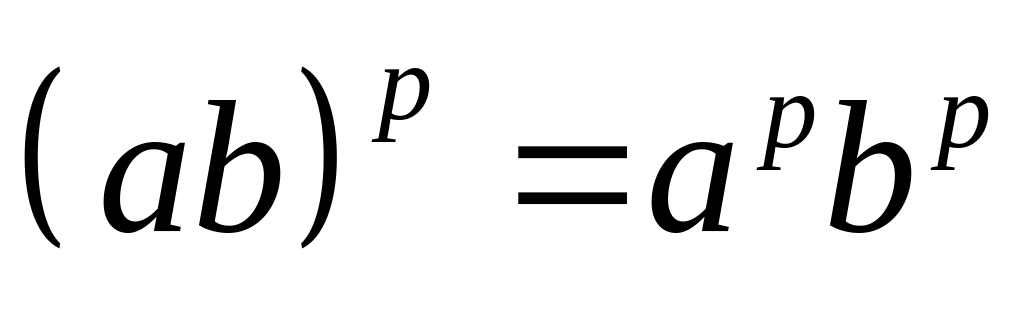 ,
,
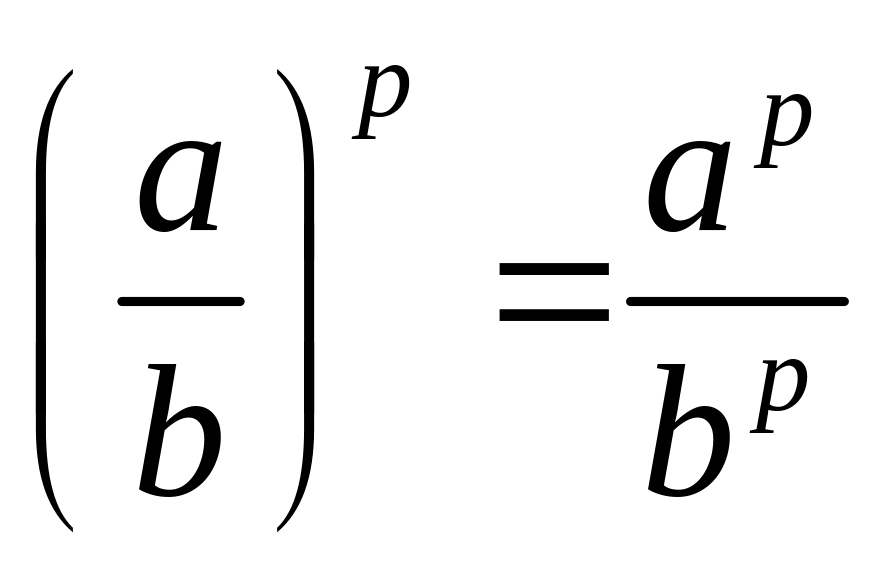 .
.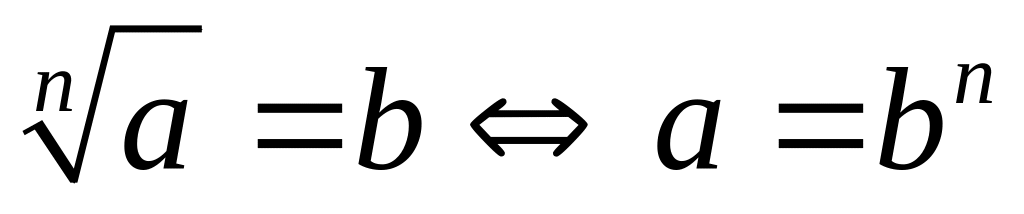 и
и
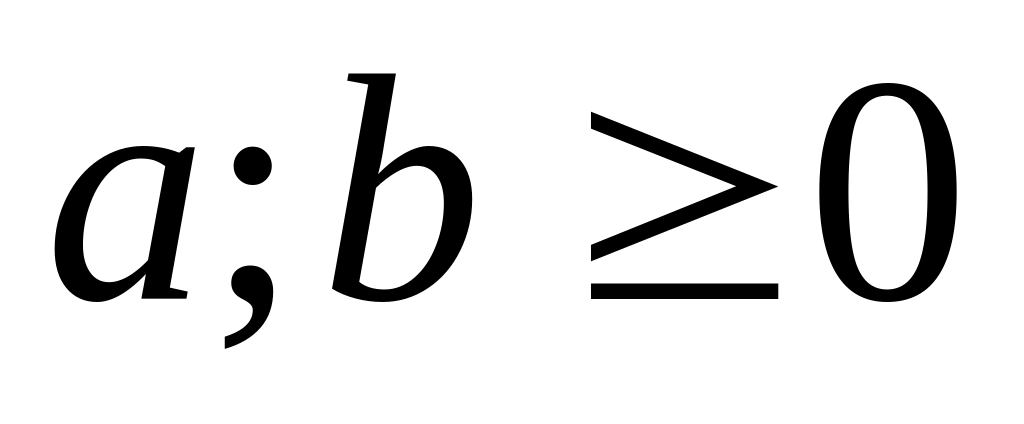 при
при
 - чётном;
при
- нечётном.
- чётном;
при
- нечётном. ,
если
;
,
если
;
 не определено;
не определено;
 ;
;
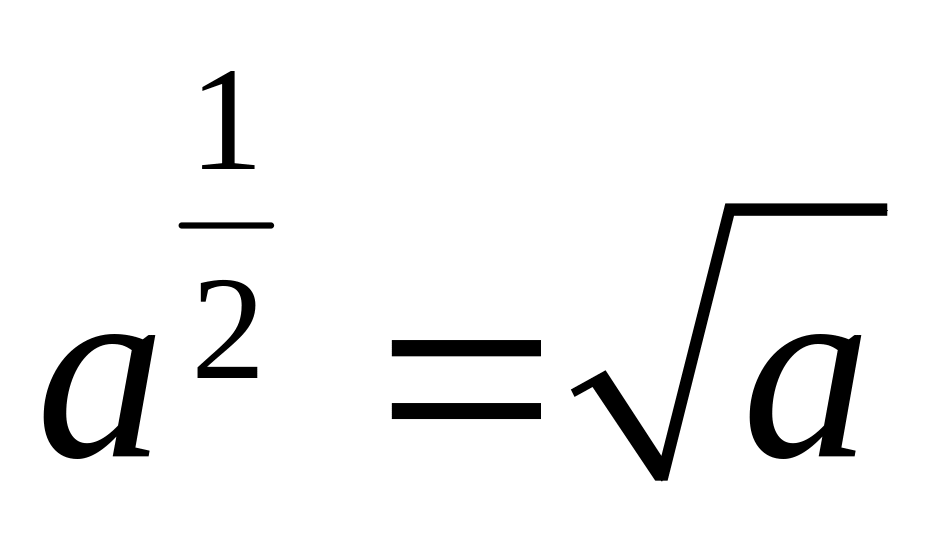 ;
;
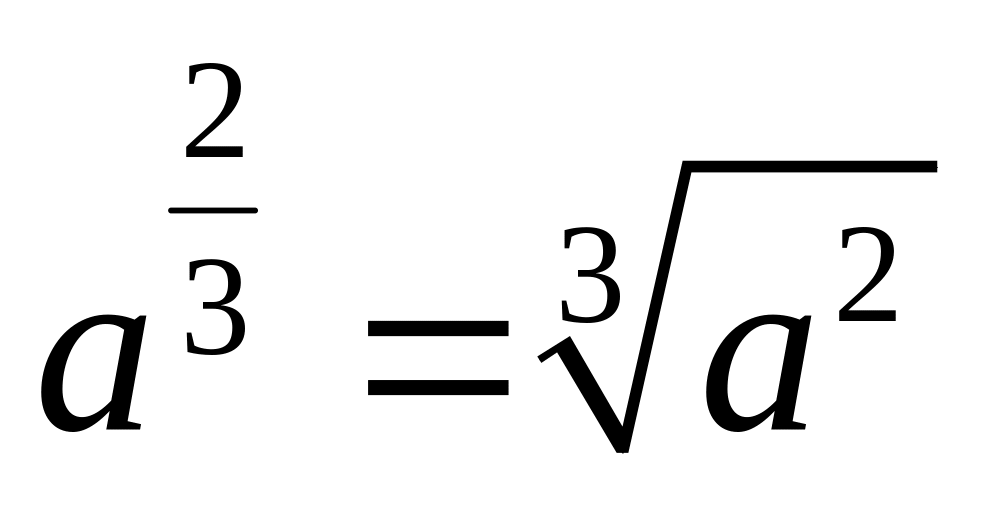 ,
и т. п.
,
и т. п.
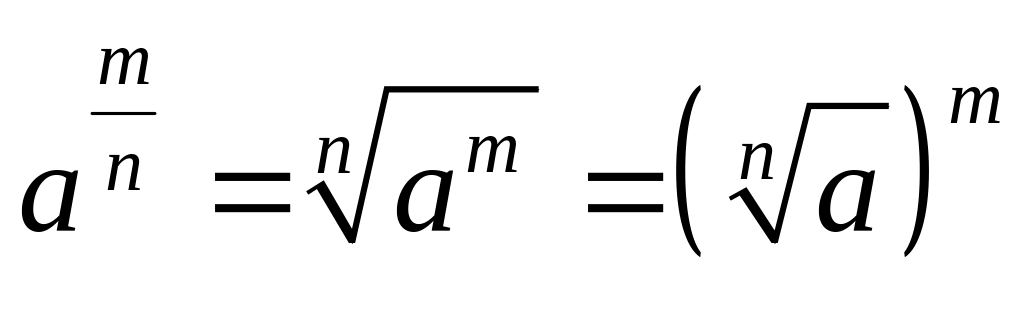 ,
,
 .
При
:
.
При
:
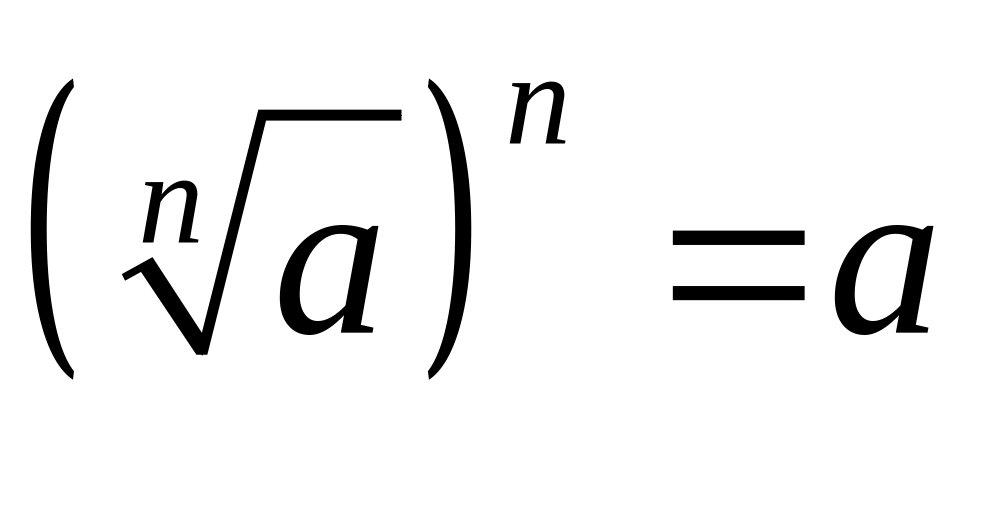 ;
;
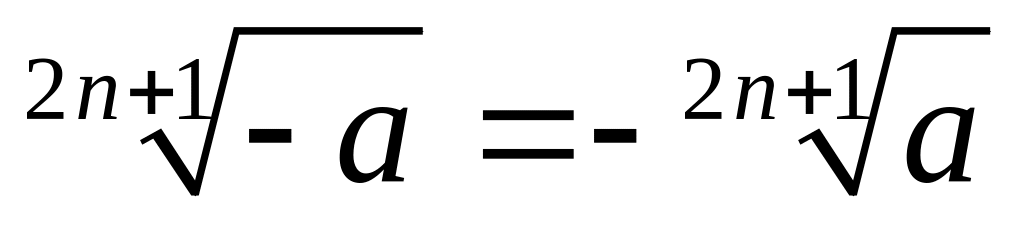 .
.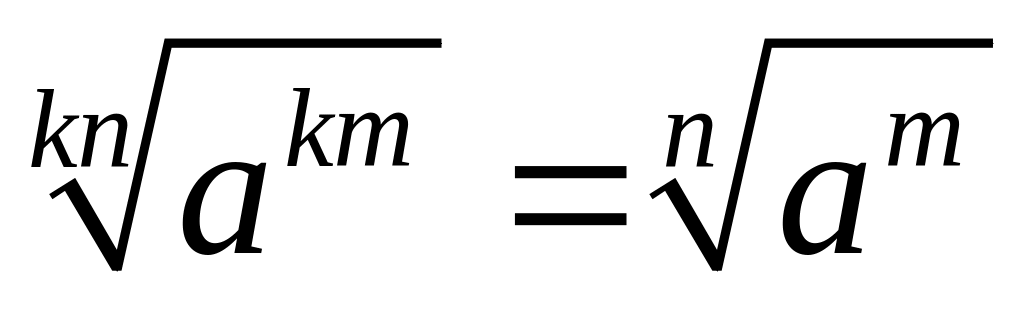 ;
;
 ;
;
 ;
;
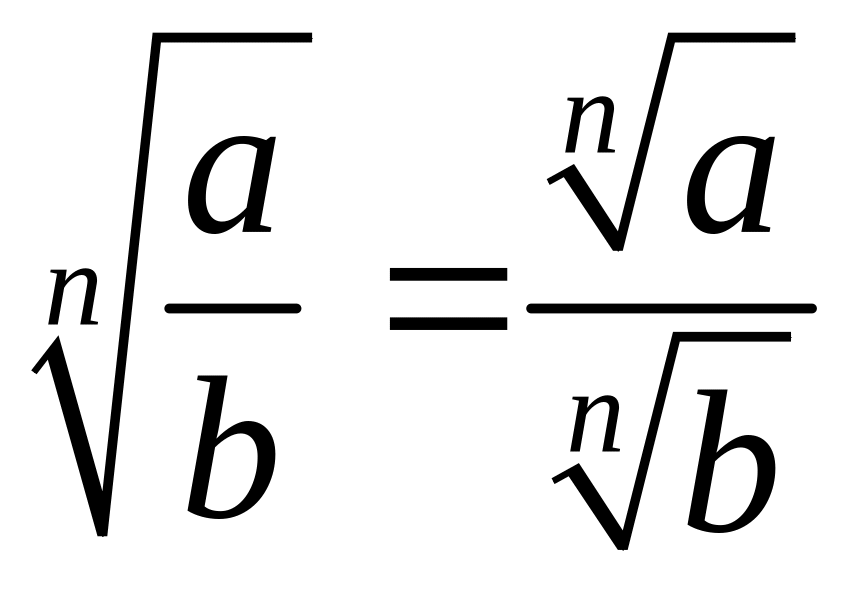 ;
;
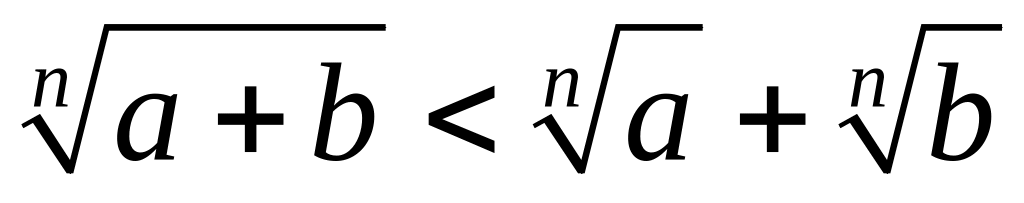 .
.Формула сложного корня:
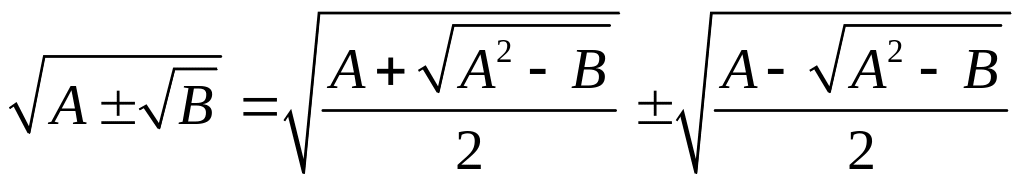 .
.
§ 7. Арифметическая прогрессия.
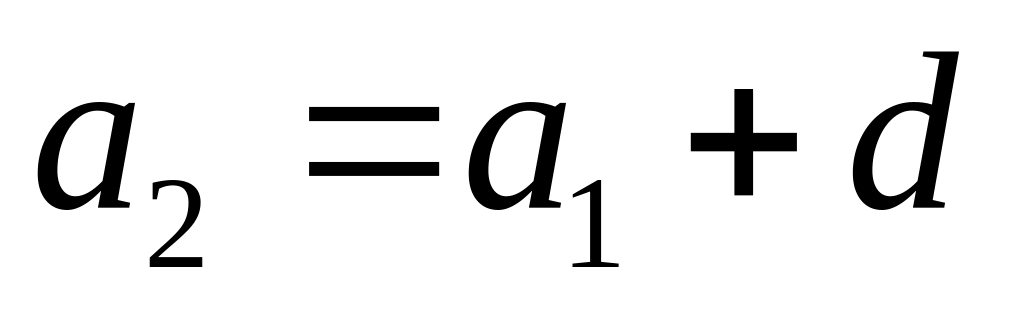 ;
;
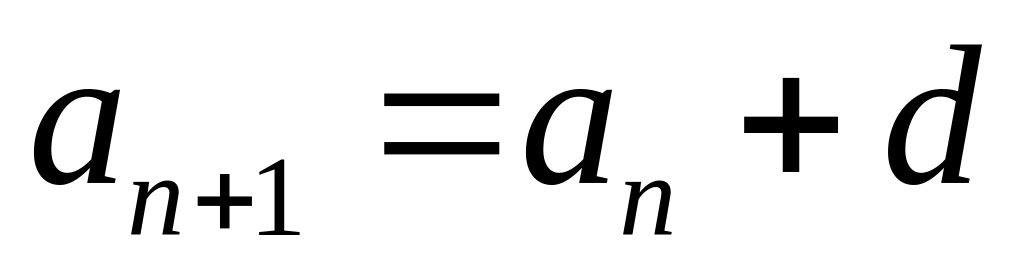 ,
,
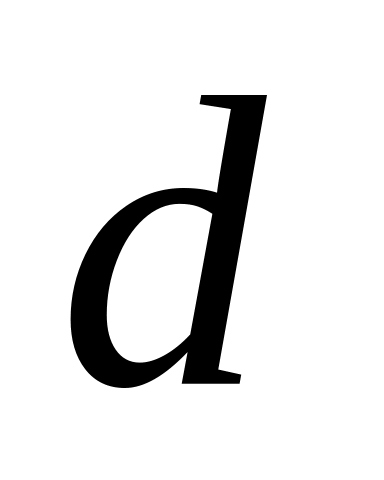 - разность прогрессии;
- разность прогрессии;
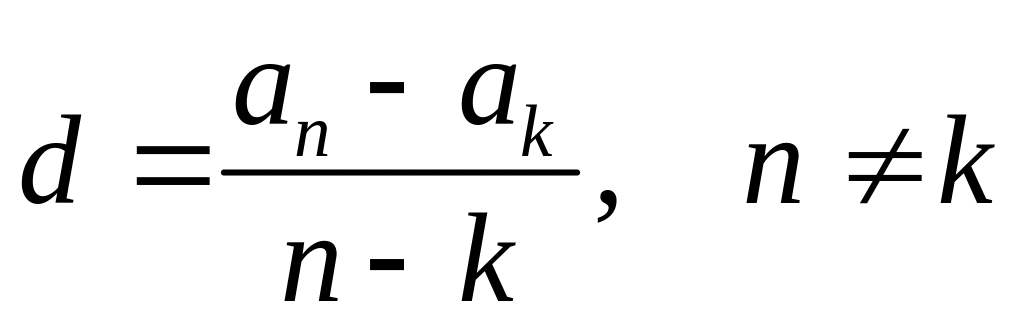 .
.Если
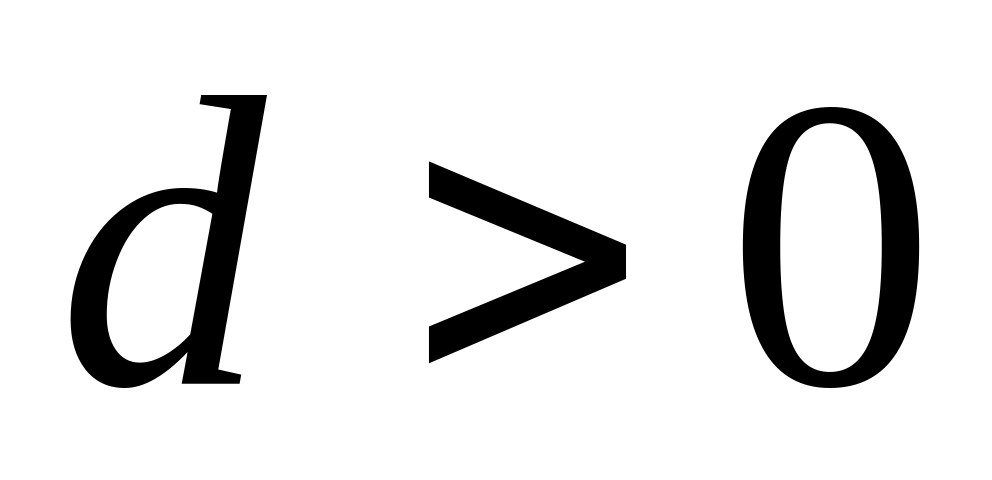 ,
то прогрессия возрастающая, если
,
то прогрессия возрастающая, если
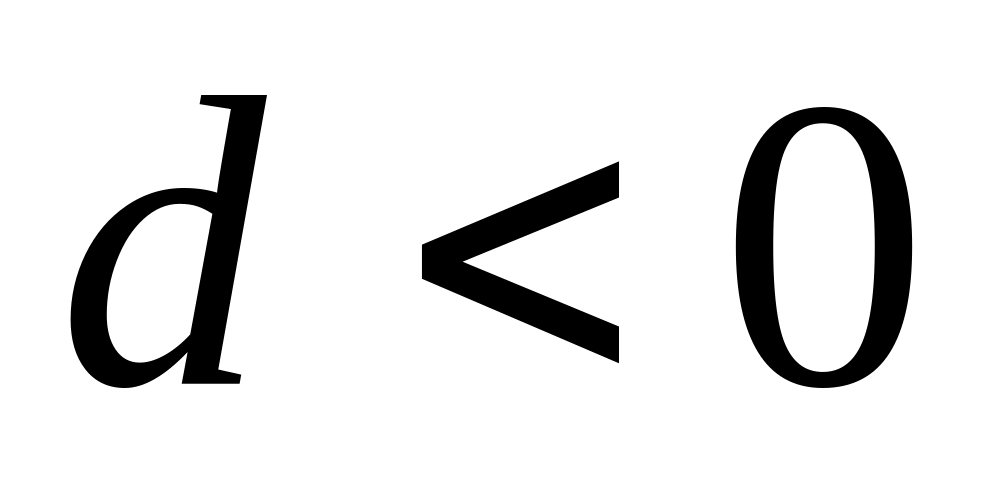 ,
то убывающая.
,
то убывающая.
Если
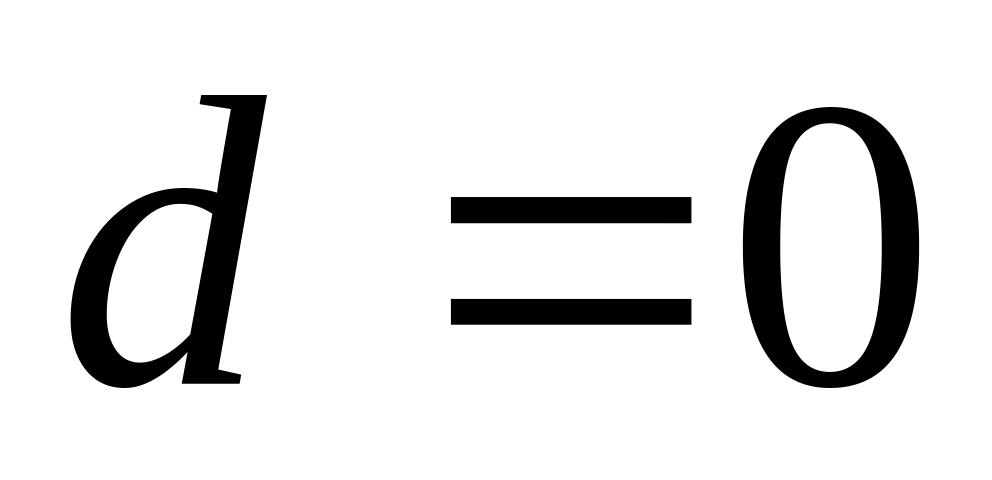 ,
то все члены прогрессии одинаковые,
т.е.
,
то все члены прогрессии одинаковые,
т.е.
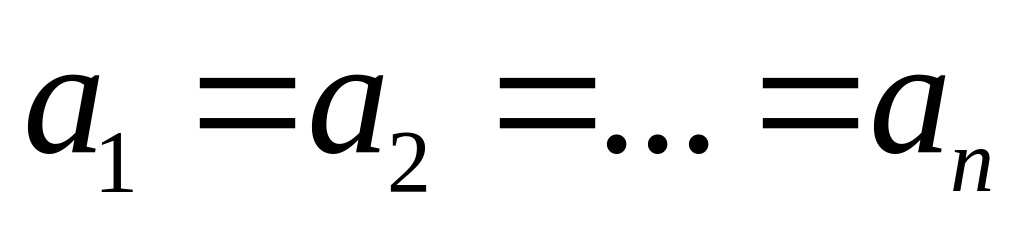 .
.Формула - го члена:
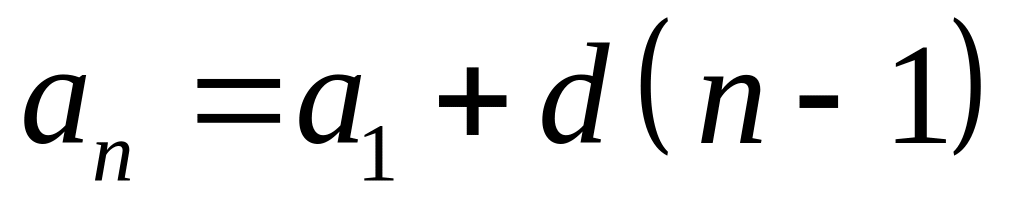 .
.Сумма первых членов арифметической прогрессии:
![]() .
.
Характеристическое свойство:
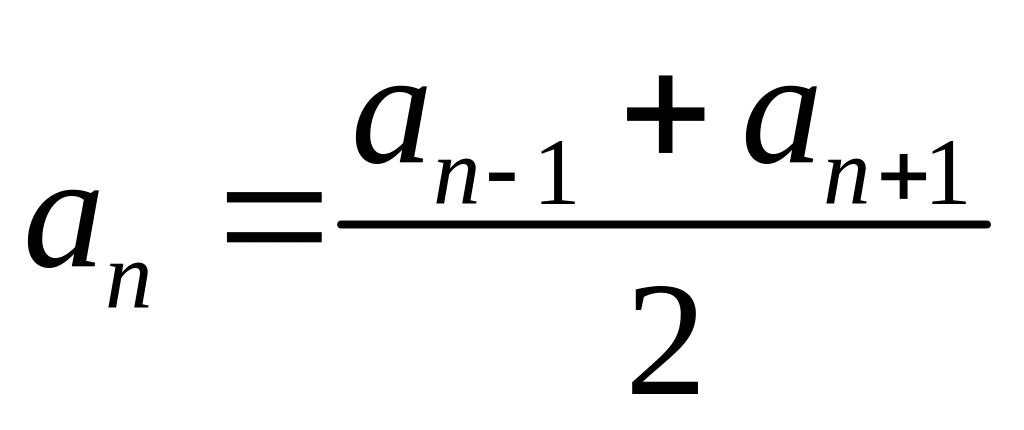 .
.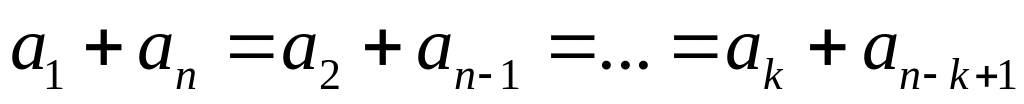 .
.Если
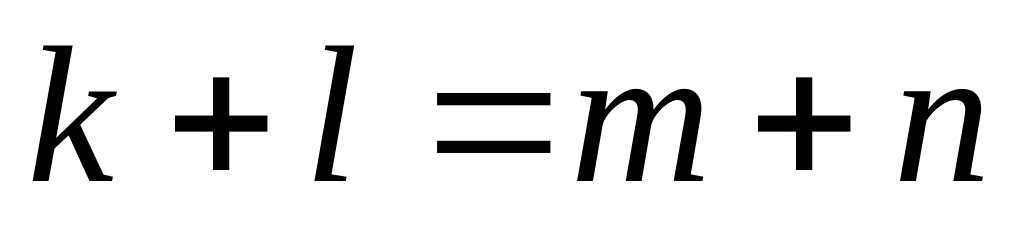 ,
то
,
то
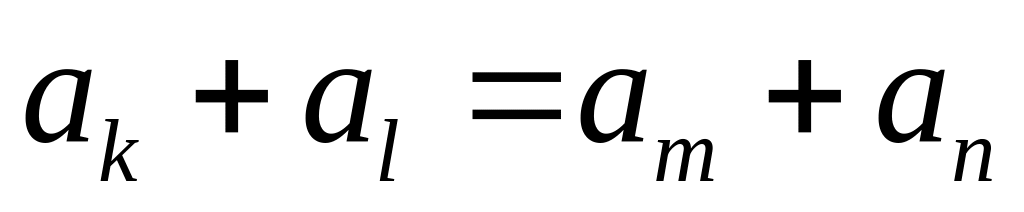 .
.
§ 8. Геометрическая прогрессия.
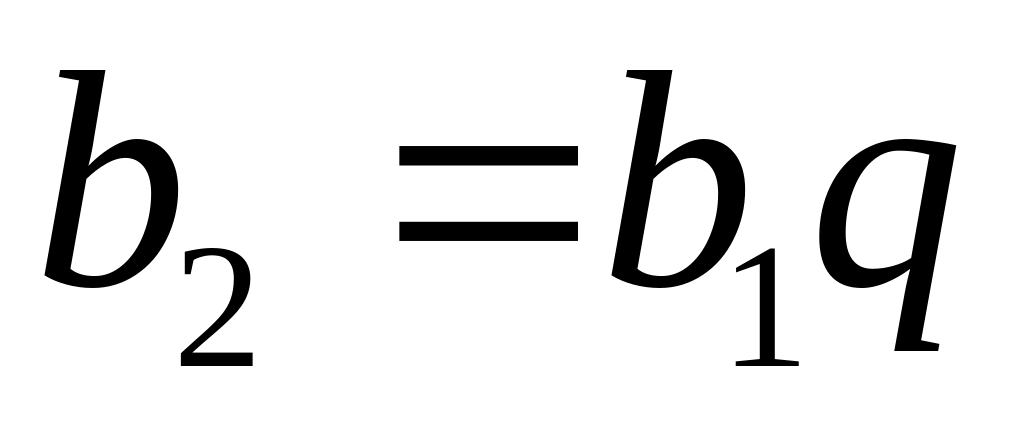 ,
,
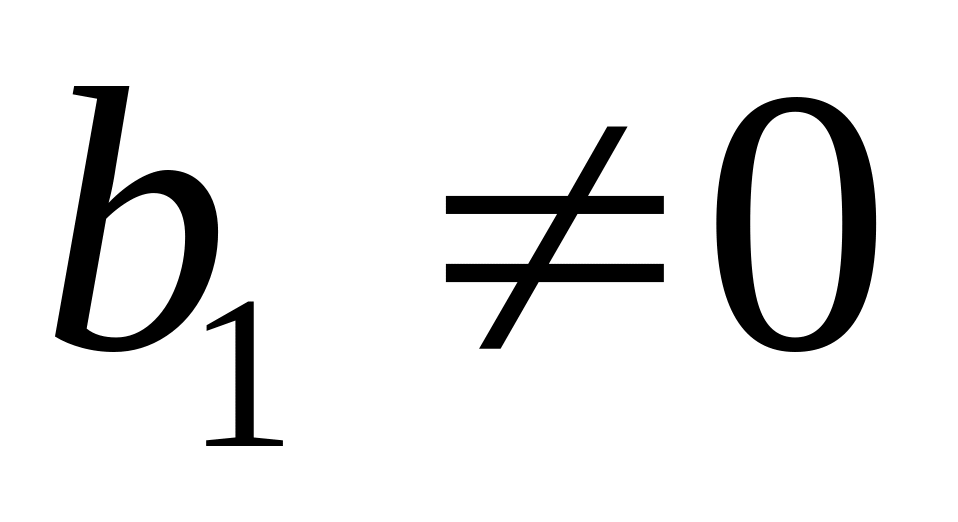 ;
;
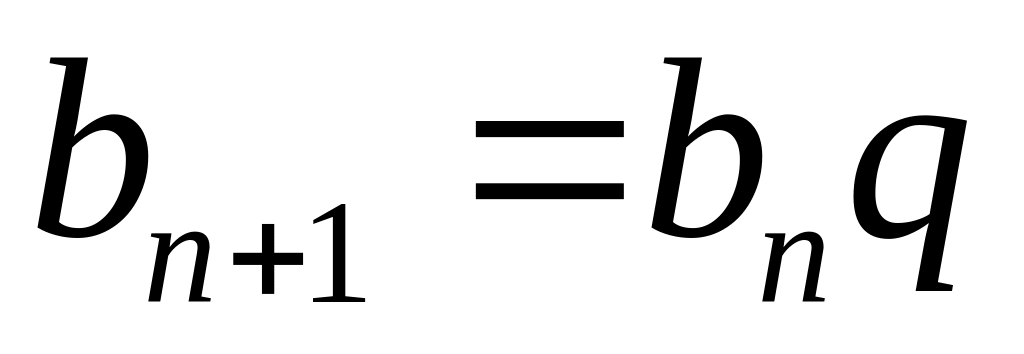 ,
,
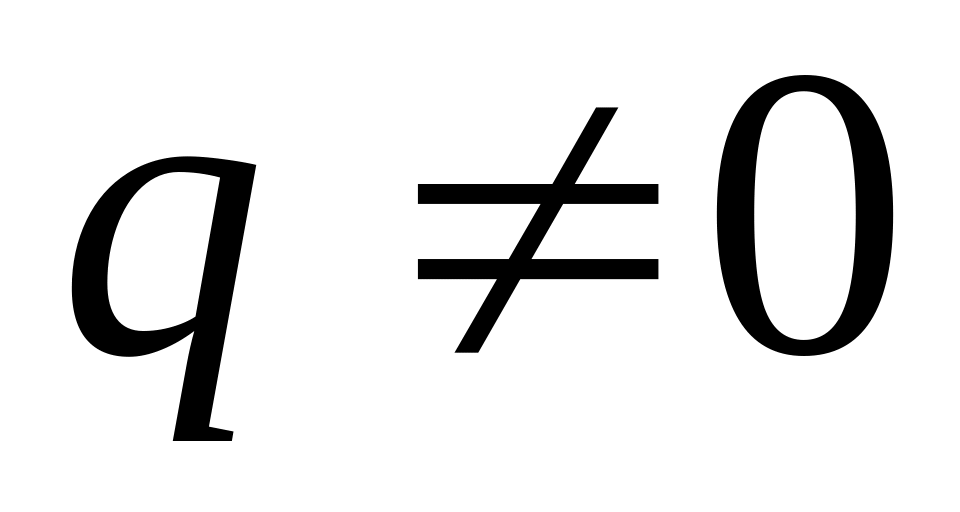 - знаменатель прогрессии.
- знаменатель прогрессии.Если
 ,
то прогрессия возрастающая; если
,
то прогрессия возрастающая; если
 ,
то убывающая.
,
то убывающая.
Если
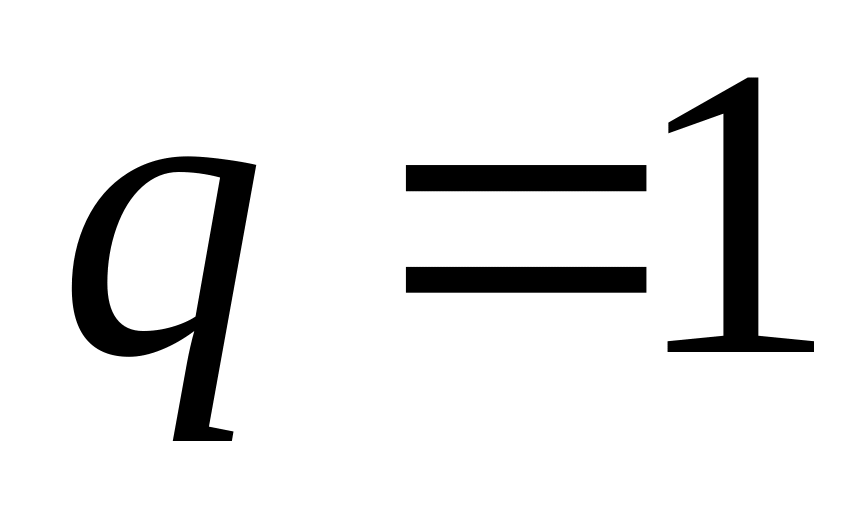 ,
то все члены прогрессии одинаковые,
т.е.
,
то все члены прогрессии одинаковые,
т.е.
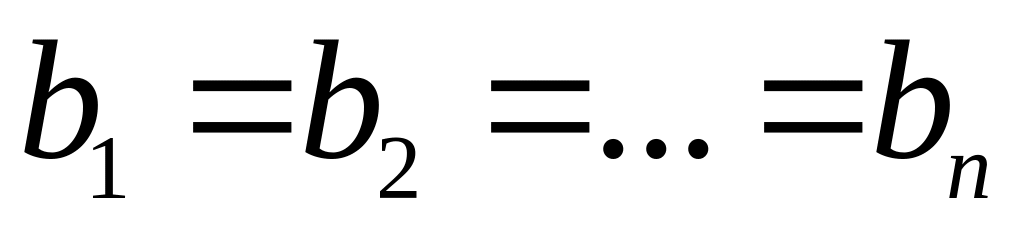 ;
;
если
![]() ,
то
,
то
![]() .
.
Формула - го члена:
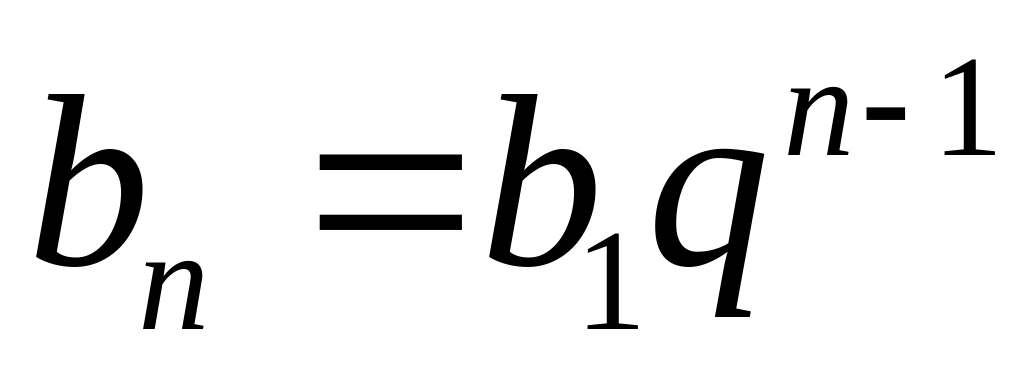 .
.Сумма первых членов геометрической прогрессии:
 ,
если
,
если
![]() ;
;
![]() ,
если
,
если
![]() .
.
Если
![]() ,
то
,
то

Характеристическое свойство:
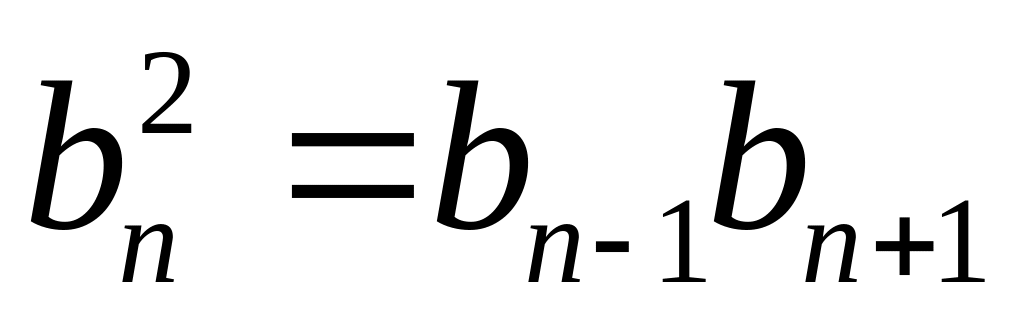 ,
или
,
или
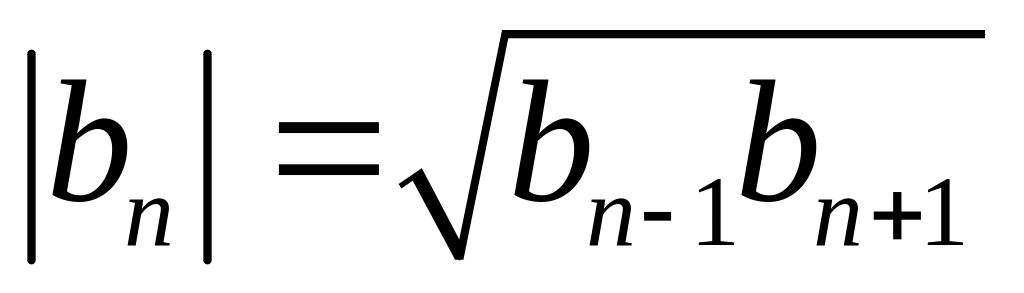 .
.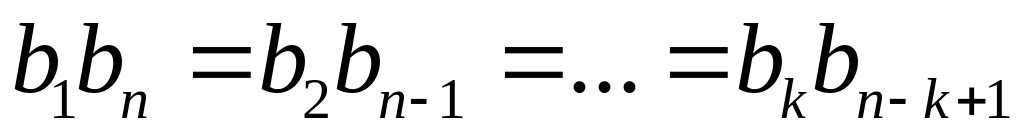 .
.Если , то
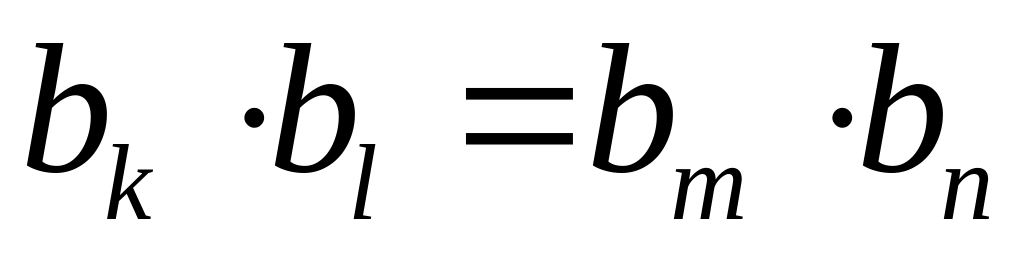 .
.Сумма бесконечно убывающей геометрической прогрессии
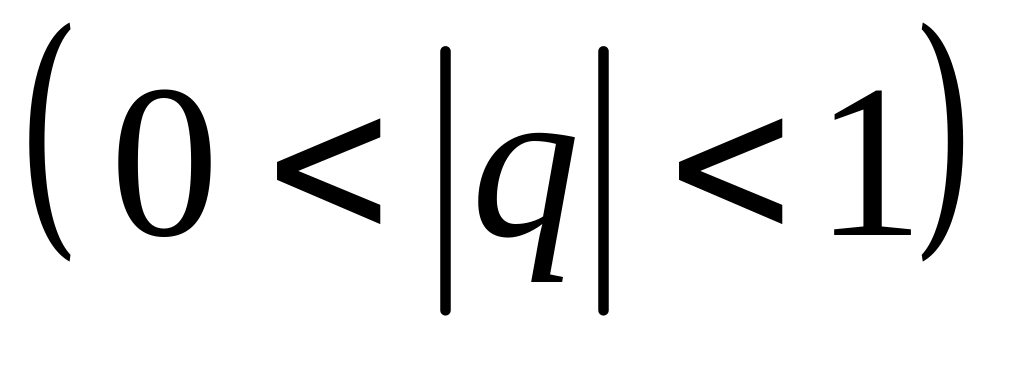 :
:
![]() .
.
§ 9. Область определения функции.
Область определения функции (ОДЗ) есть множество значений, которые может принимать независимая переменная . Для функции
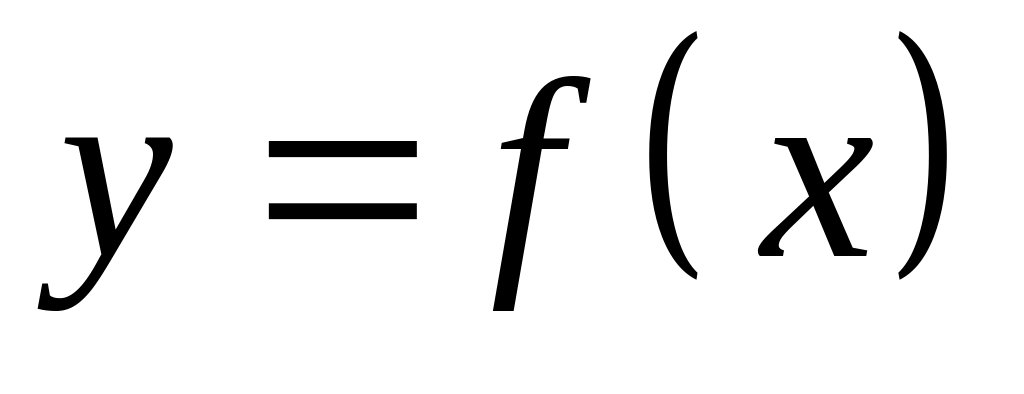 приняты обозначения
или
приняты обозначения
или
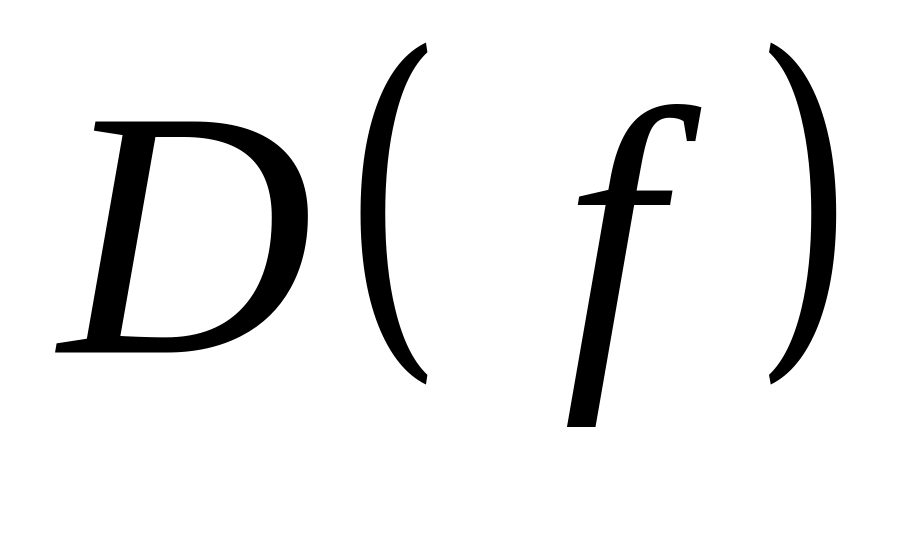 .
Для нахождения ОДЗ сложной функции
записывают систему условий для ОДЗ
каждой функции.
.
Для нахождения ОДЗ сложной функции
записывают систему условий для ОДЗ
каждой функции.На графике функции область определения находят по оси
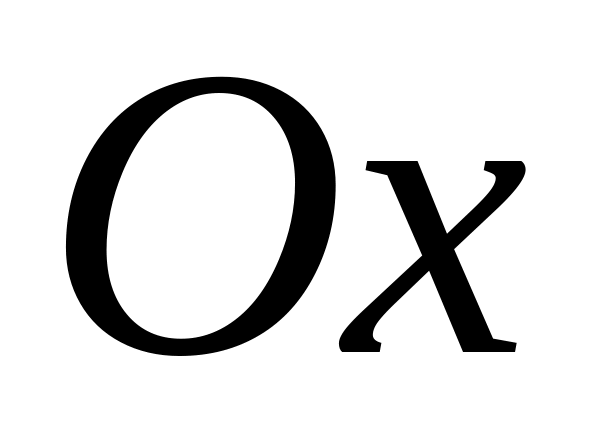 .
.Если
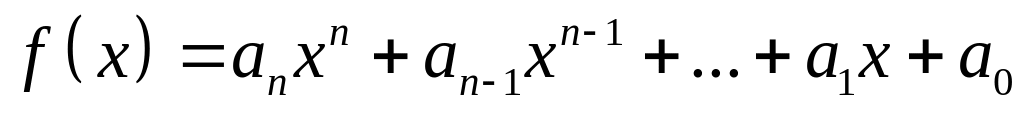 (многочлен), то
(многочлен), то
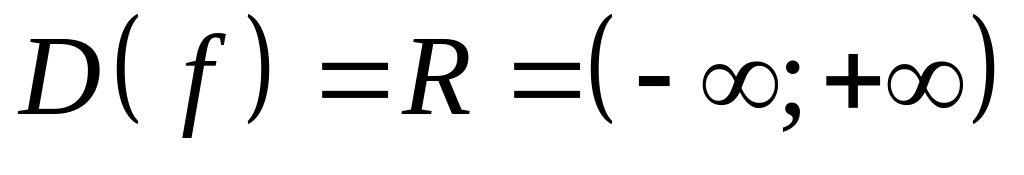 .
.Если
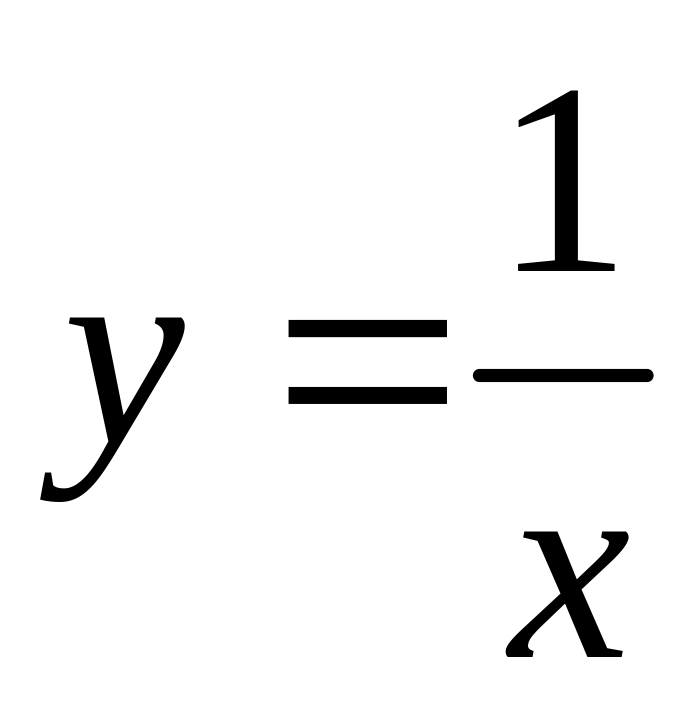 ,
то
,
то
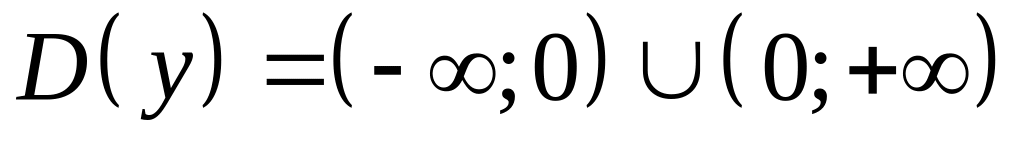 ,
или
,
или
 .
.Если
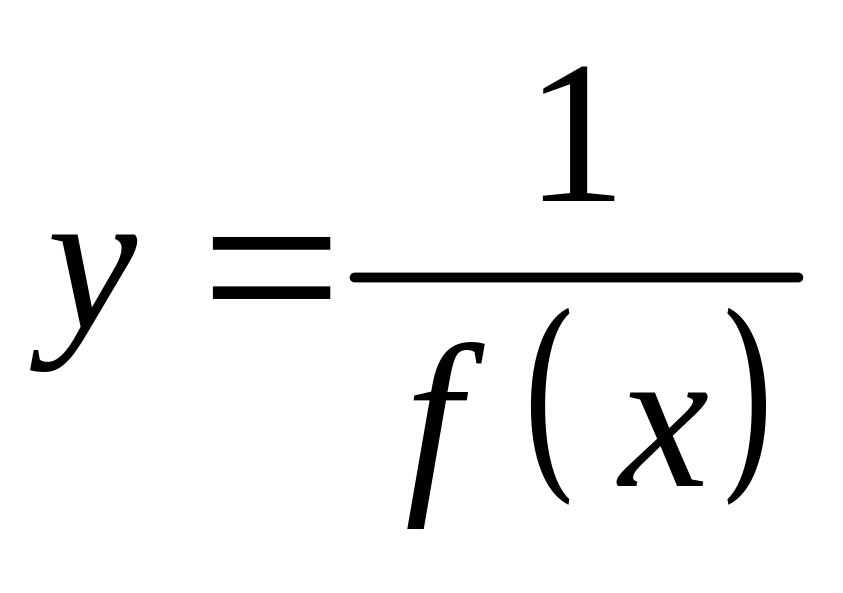 ,
то
находится из условия
,
то
находится из условия
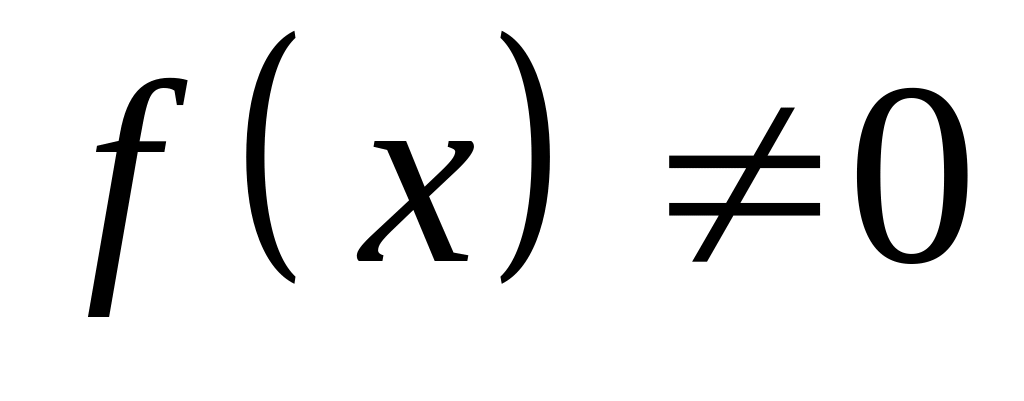 .
.Если
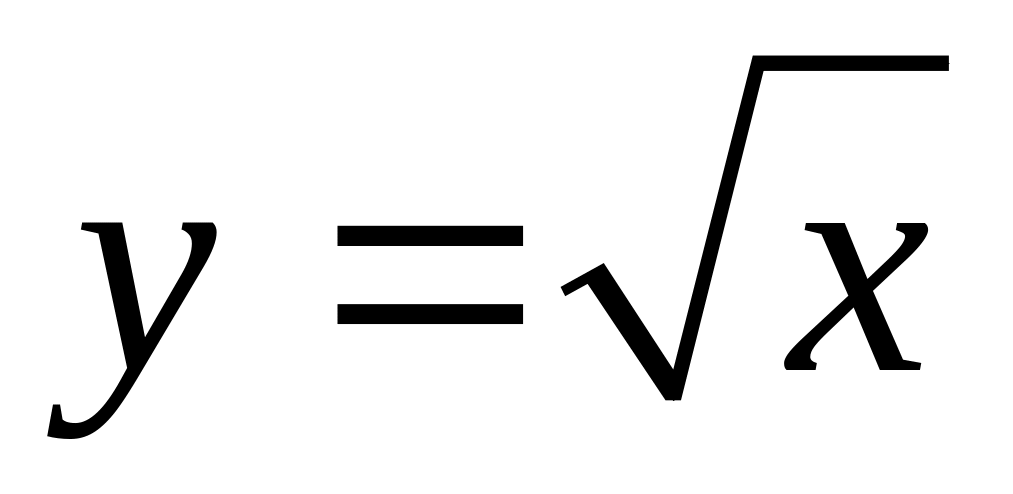 или
или
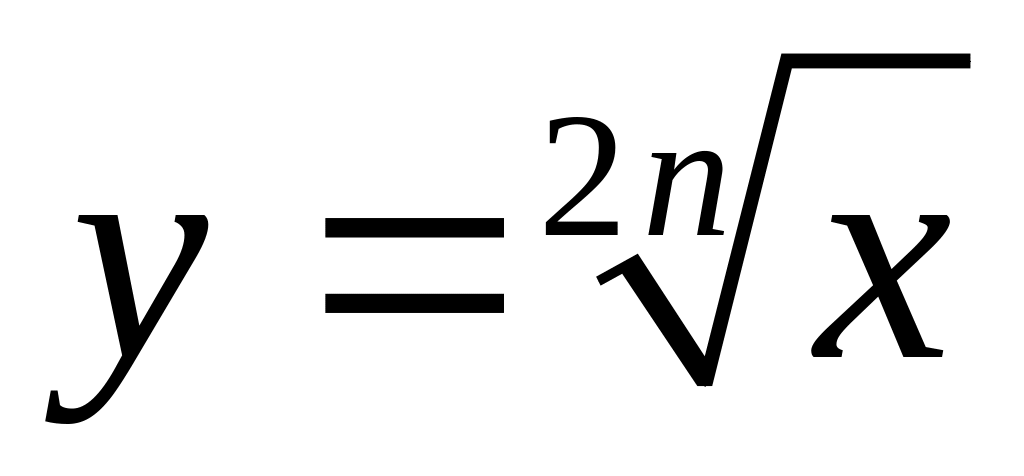 ,
то
,
то
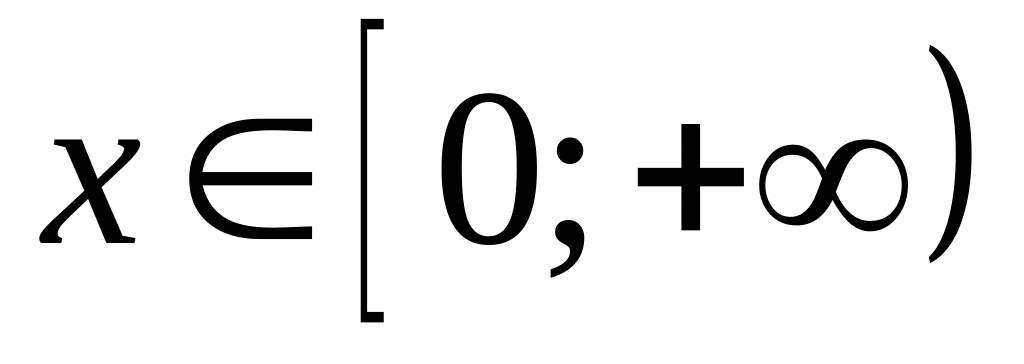 ,
или
,
или
 .
.Если
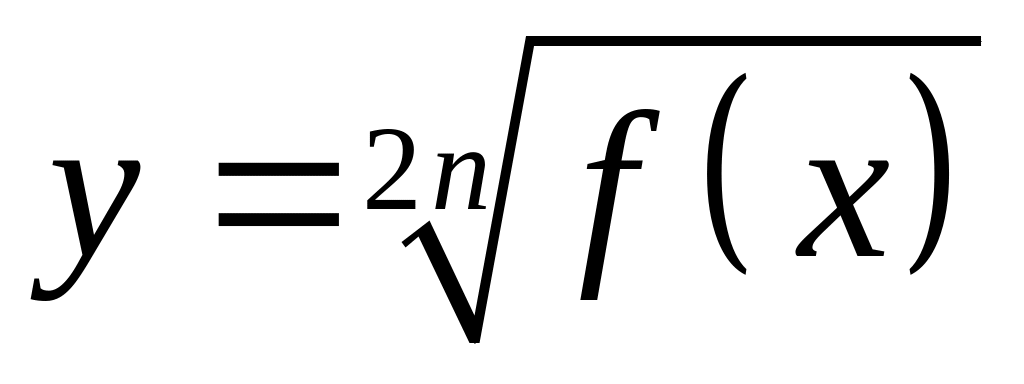 ,
то
находится из условия
,
то
находится из условия
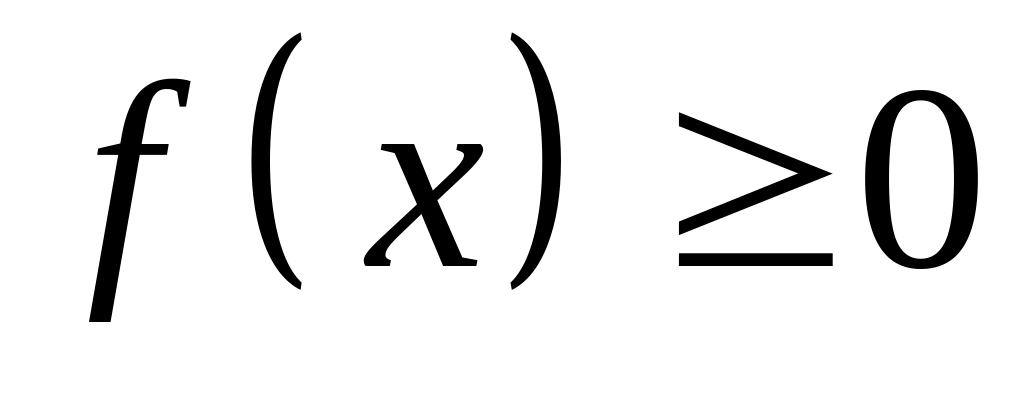 .
.Если
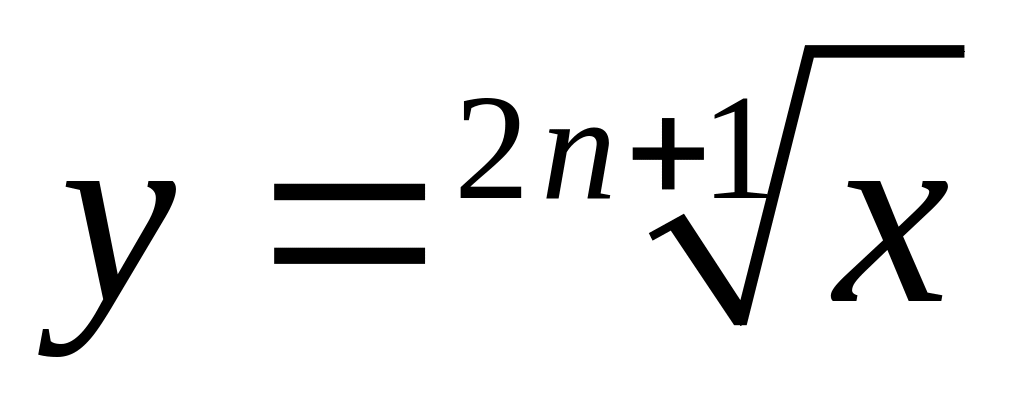 ,
то
,
то
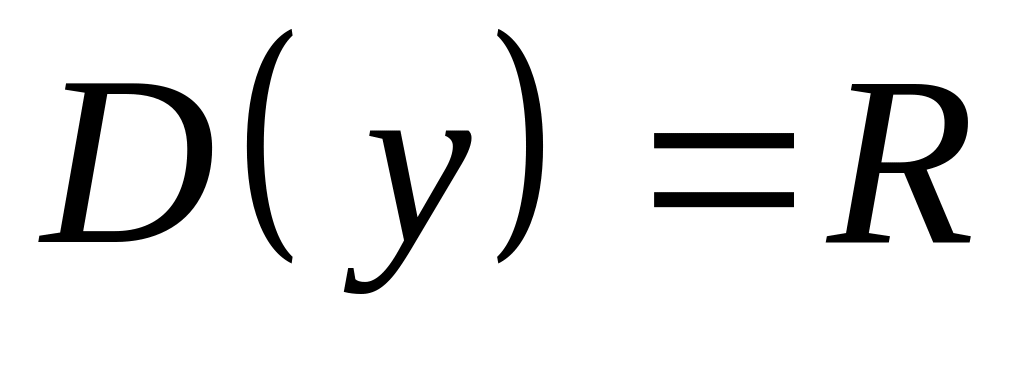 .
.Если
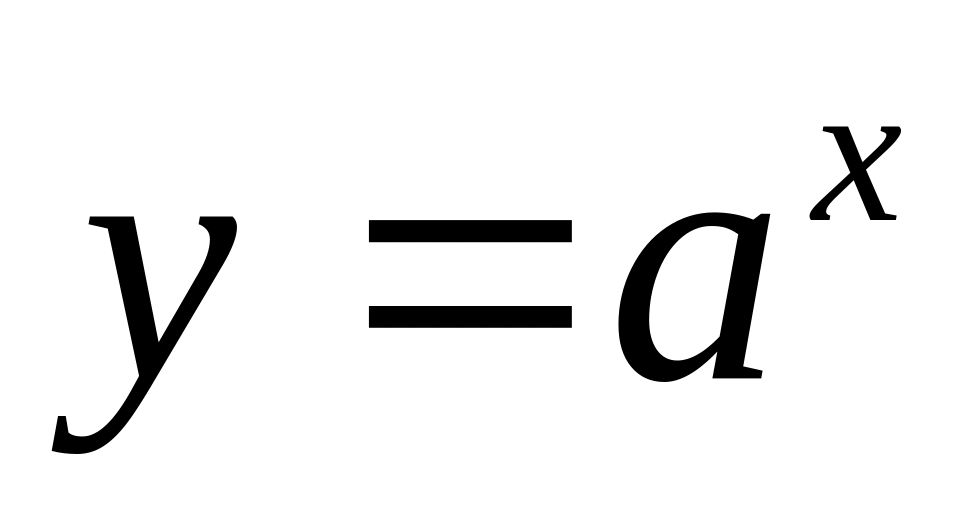 ,
то
.
,
то
.Если
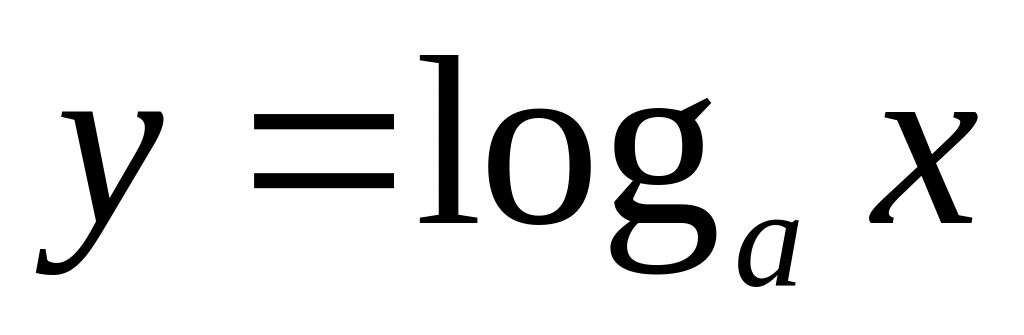 ,
то
,
то
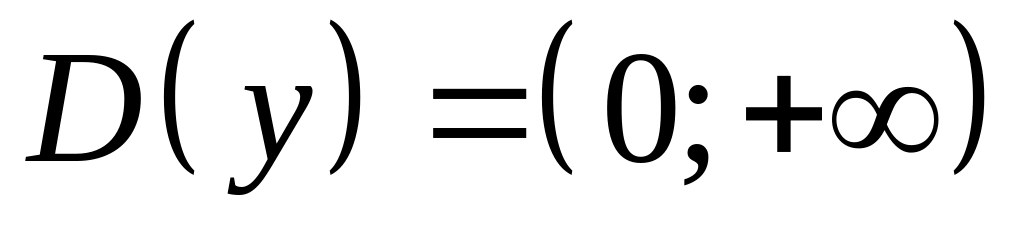 ,
или
,
или
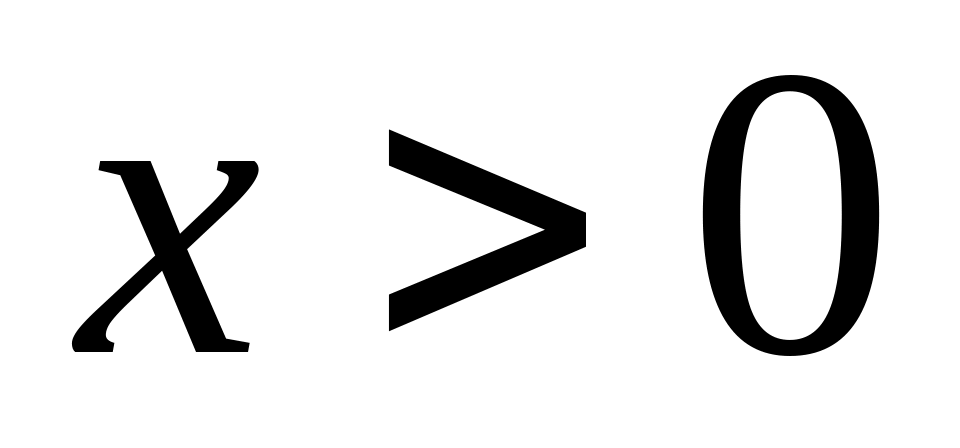 .
.Если
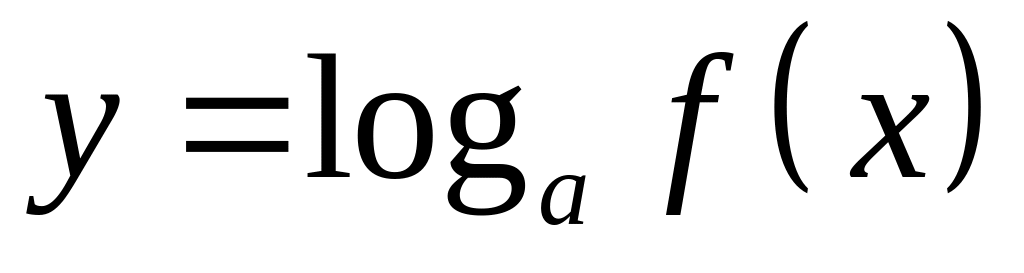 ,
то
находится из условия
,
то
находится из условия
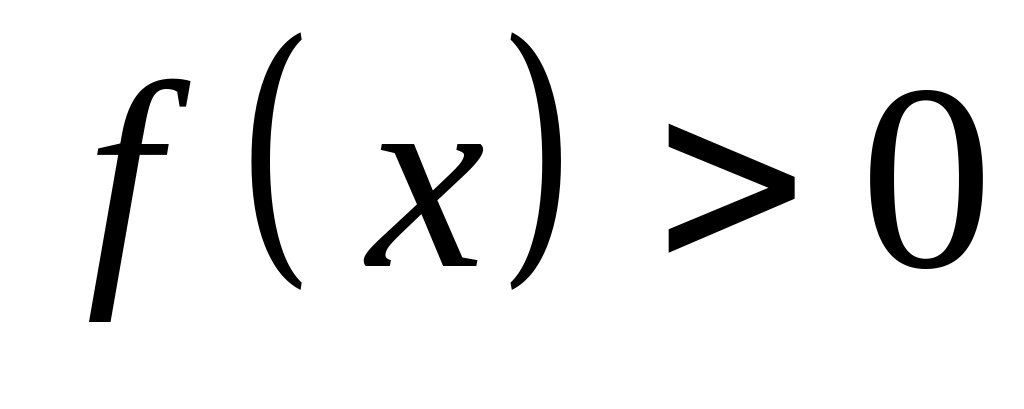 .
.
