2.4. Решение уравнений Блоха при возбуждении сложными сигналами
В
общем случае система уравнений Блоха
(1.21) представляет собой систему
неоднородных линейных дифференциальных
уравнений первого порядка с зависимыми
от времени коэффициентами. Аналитическое
решение в этом случае, как правило,
получить не удается. Однако можно найти
приближенное решение. Для этого
предположим, что длительность сигнала
.
Тогда в уравнениях (1.21) можно не учитывать
релаксационные члены и уравнения примут
вид
;
;
(2.17)
.
Пусть
сигнал
действует на симметричном интервале
времени
.
Введем новый вектор
,
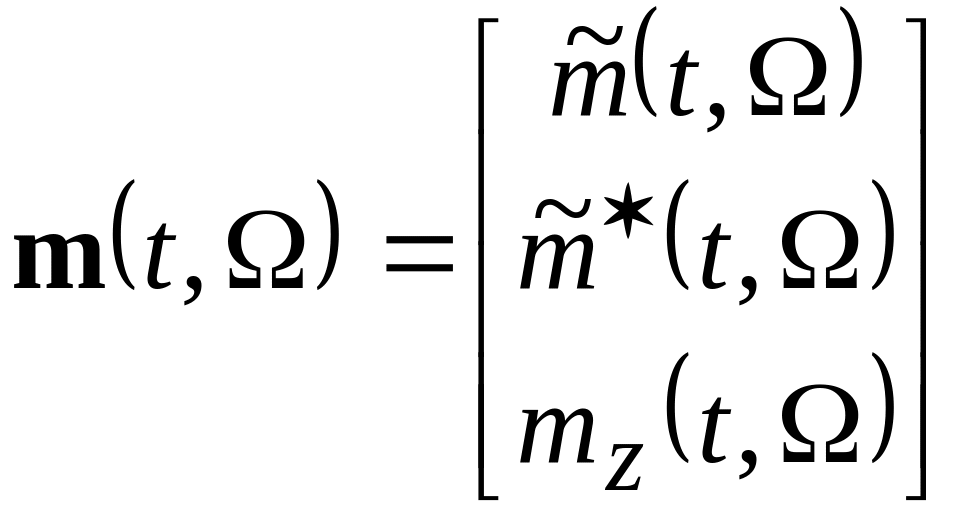связанный
с исходным
матричным соотношением
(2.18)
где
.
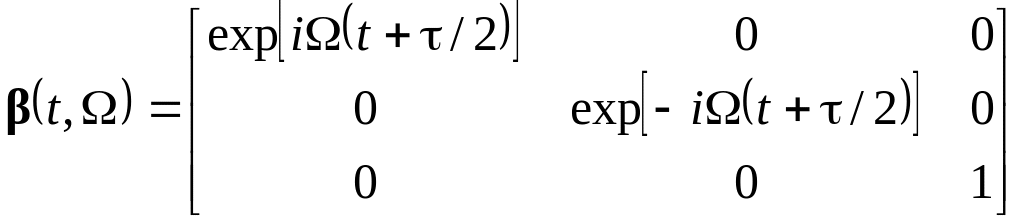После подстановки (2.18) в (2.17) получим новую систему дифференциальных уравнений
;
;
.
Эту систему можно представить в матричной форме:
.
Решение
в момент окончания импульса
при известных начальных условиях
определяется матричным уравнением
.
(2.19)
Матрицу
можно определить по формуле Магнуса
где первый член суммы имеет вид
-
спектральная плотность комплексной
огибающей сигнала возбуждения.
Пусть
,
что соответствует малосигнальному или
линейному режиму возбуждения. Представим
матричную экспоненту рядом
(2.20)
где I- единичная матрица.
Практической
границей малосигнального режима принято
считать уровень спектра
.
Ограничившись в (6.20) тремя первыми
членами, получим
.
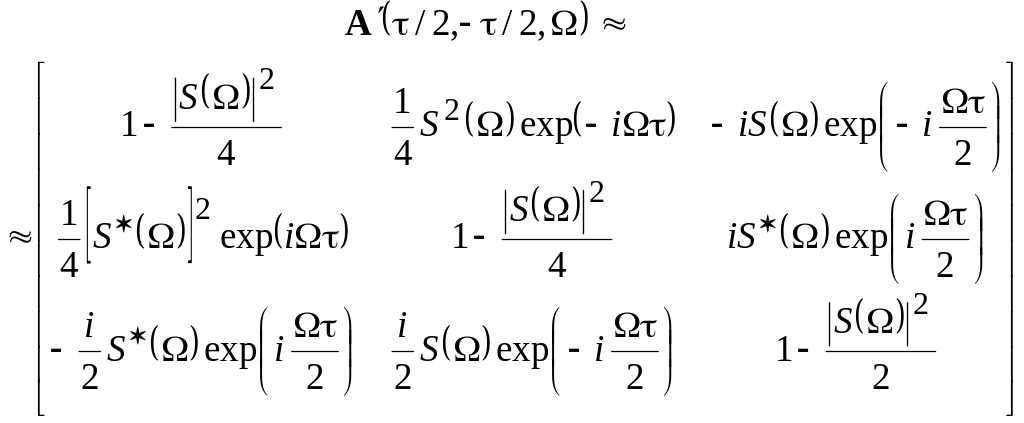Возвращаясь
к старым переменным, на основании (2.18),
(2.19), а также с учетом того, что
,
получаем для малосигнального режима
возбуждения
где
переходная матрица
.
(2.21)
Аналогичное решение может быть получено и методом последовательных приближений.
Используя
(2.21), можно определить комплексную
огибающую двухимпульсного эха в
малосигнальном режиме при возбуждении
двумя произвольными по форме сигналами
со спектрами комплексных огибающих
.
Для этого необходимо соответствующие
элементы матрицы A
подставить в (11.13). В результате получим
.
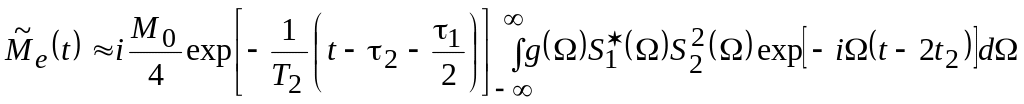Для коротких по сравнению с временами релаксации импульсов это выражение можно упростить
.
(2.22)
Если взять преобразование Фурье от (6.22), то спектральная плотность комплексной огибающей двухимпульсного эха будет равна
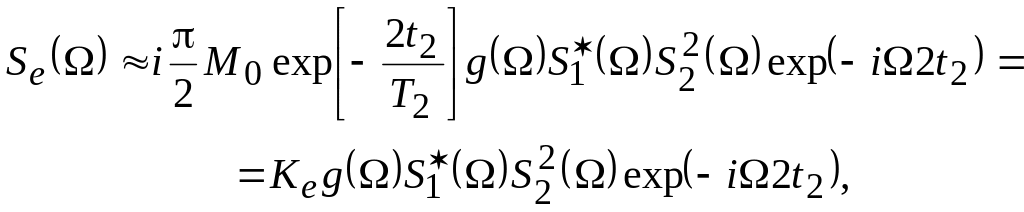(2.23)
где
.
Подставив соответствующие элементы матрицы A (6.21) в (6.15), при тех же ограничениях получим комплексную огибающую стимулированного эха
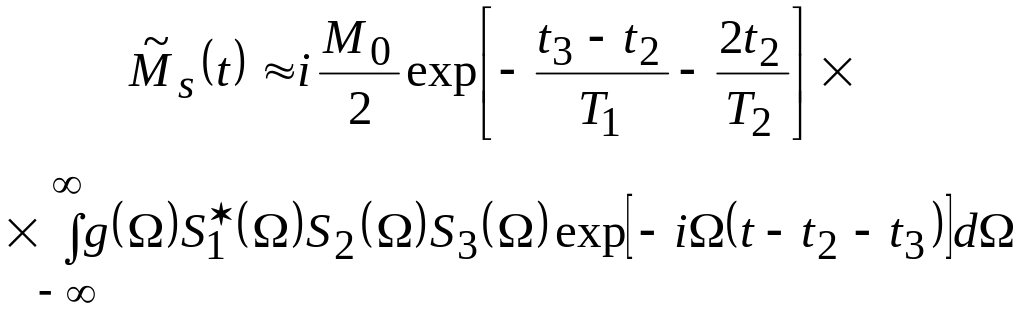(2.24)
и ее спектральную плотность
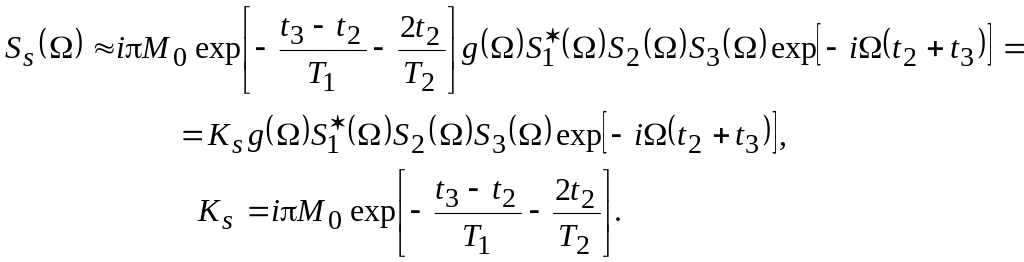
(2.25)
Уравнения Блоха (1.21) представляют собой систему линейных дифференциальных уравнений в общем случае с зависящими от времени коэффициентами, которые определяются видом сигналов возбуждения. Точное аналитическое решение можно найти лишь в тех случаях, когда эти коэффициенты не зависят от времени, либо являются кусочно-независимыми.
Так
известно решение уравнений Блоха для
простых прямоугольных радиоимпульсов,
длительность которых
.
На его основе можно получать также
соответствующие аналитические решения
для случая возбуждения спиновых систем
фазоманипулированными сигналами,
комплексную огибающую которых можно
рассматривать как кусочно-независимую
функцию времени.
Трехимпульсный режим возбуждения и трехимпульсное эхо нашли наиболее широкое применение в спиновых процессорах, основанных на эффекте эха.
Наряду с двух- и трехимпульсными режимами возбуждения эхо существуют также алгоритмы с большим количеством импульсов возбуждения.