1.2. Уравнения Блоха

Если поместить парамагнитное вещество в постоянное магнитное поле B_а=B₀e_z, то в состоянии равновесия индуцируется намагниченность, параллельная приложенному магнитному полю

M_z = M₀ = ₀B₀,

где ₀ – статическая магнитная восприимчивость.

Выведенный из состояния равновесия вектор намагниченности начинает вращаться вокруг продольной оси z, причем этот процесс в принятой модели будет продолжаться бесконечно.

Однако в реальных ситуациях естественно ожидать, что существует механизм возврата вектора намагниченности с течением времени в исходное состояние равновесия параллельно полю B₀e_z. Такой механизм связан, главным образом, с взаимодействием магнитных моментов ядер с решеткой и называется спин-решеточной или продольной релаксацией. При этом предполагается, что продольная компонента M_z приближается к равновесному значению со скоростью, пропорциональной отклонению M_z от равновесного значения M₀ (рис. 1.2):

. (1.9)

Рис. 1.2 Намагничивание образца в продольном магнитном поле

Введенный параметр T₁ называют временем спин-решеточной или продольной релаксации.

Если ненамагниченное вещество, у которого M_x=M_y=M_z=0, поместить в момент времени t=0 в магнитное поле B₀e_z, то, проинтегрировав (1.9), получим решение , в соответствии с которым идет процесс установления стационарного состояния.

При установлении стационарного состояния должны уменьшаться поперечные компоненты M_x и M_y вектора намагниченности, выведенного из состояния равновесия. Этот процесс связан с взаимодействием магнитных моментов ядер между собой и называется спин-спиновой или поперечной релаксацией. Затухание поперечных компонент описывается уравнениями

; (1.10)

, (1.11)

где T₂ – параметр, называемый временем спин-спиновой или поперечной релаксации. С течением времени компоненты M_x и M_y вектора намагниченности, прецессирующего вокруг оси x, затухают в принятой модели по экспоненциальному закону .

Модифицированные уравнения движения вектора намагниченности M во внешнем магнитном поле B_а c учетом спин-спинового и спин-решеточного взаимодействия в форме (1.9)-(1.11) называются уравнениями Блоха:

; ; (1.12)

.

Времена продольной и поперечной релаксации связаны соотношением и зависят от вида ядер и от условий, в которых они находятся.

Необходимыми условиями существования эха, как это уже упоминалось, являются нелинейность в процессе взаимодействия поля с веществом и неоднородность параметров среды. Примером первого условия для спинового эха является нелинейная зависимость между вектором намагниченности и возбуждающим магнитным полем. Второе условие соблюдается, если индукция поляризующего магнитного поля неоднородна в объеме образца, помещенного в это поле (ранее рассматривалось однородное поляризующее магнитное поле ). В силу неоднородности магнитного поля резонансная частота магнитных моментов ядер в отличие от однородного случая (1.4) будет также неоднородной .

Введем функцию , описывающую плотность вероятности распределения магнитных моментов по частоте и называемую функцией формы неоднородно уширенной линии поглощения. Эта функция удовлетворяет условию нормировки

. Рассмотрим группу магнитных моментов, частота которых лежит в бесконечно узкой полосе частот вокруг частоты , и назовем ее изохроматой. Статический магнитный момент изохроматы будет равен

. (1.13)

Статическая намагниченность всех изохроматических групп находится интегрированием (5.13) по частоте:

. (1.14)

Среднее значение частоты магнитного резонанса обозначим , где - среднее значение в объеме образца, а ширину неоднородно уширенной линии поглощения ЯМР обозначим (рис. 1.3).

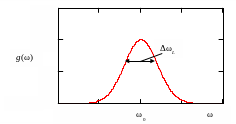
Рис.1.3 Неоднородно уширенная линия поглощения

Чтобы вывести магнитные моменты из состояния термодинамического равновесия, наряду с постоянным поляризующим магнитным полем , задающим направление продольной оси, к образцу прикладывается переменное магнитное поле с индукцией и частотой ₀ в поперечной плоскости. Для эффективного взаимодействия с вектором намагниченности это поле должно иметь круговую поляризацию, совпадающую с направлением прецессии вектора намагниченности.

Обычно же возбуждение спиновой системы осуществляется линейно-поляризованным полем

, (1.15)

где - функции, описывающие законы изменения амплитуды и фазы колебания.

Это линейно-поляризованное колебание можно представить в виде суммы двух колебаний с круговой поляризацией, вращающихся в разные стороны. Можно показать, что вблизи резонанса составляющей поля, вращающейся в противоположную по отношению к направлению прецессии сторону, можно пренебречь. Тогда можно считать, что в поперечной плоскости действует поле с круговой поляризацией

, (1.16)

с амплитудой в два раза меньшей, чем в (1.15) (рис. 1.4).

Рис. 1.4 Представление линейной поляризации в виде двух круговых

В дальнейшем удобно перейти в новую систему координат с осями , вращающуюся вокруг оси с частотой в направлении вращения поля (1.16) (рис. 1.5).

Рис. 1.5 Вращающаяся система координат

Связь производных в неподвижной и вращающейся системах координат имеет вид

, (1.17)

где ( )_вр – производная во вращающейся системе координат, а

₀ =- ₀e_z. (1.18)

С учетом (5.8) можно переписать (5.17) в виде

, (1.19)

где

. (1.20)

На основании (1.18)-(1.20) можно представить уравнения Блоха (1.12) во вращающейся системе координат:

;

; ,

где .

Введем комплексные поперечные компоненты:

; ;

; .

Для введенных компонент уравнения Блоха во вращающейся системе координат примут вид

;

; (1.21)

.

Система (1.21) в общем случае объединяет линейные дифференциальные уравнения с переменными коэффициентами и не имеет точного аналитического решения.

Решение уравнений Блоха (1.21) для свободных интервалов времени, когда при заданных начальных условиях M(t₀, Ω), может быть представлено в матричной форме

(1.22) ,

.

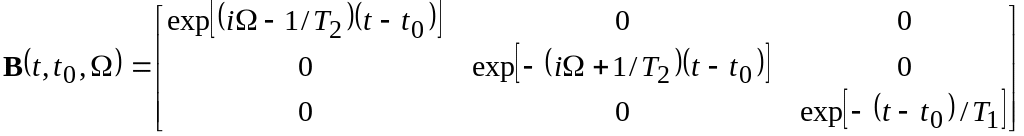Из (1.22) следует, что поперечные компоненты совершают круговое движение вокруг продольной оси и одновременно уменьшаются по амплитуде по экспоненциальному закону

.

П родольная компонента вектора намагниченности стремится к равновесному значению (рис. 1.6).

.

Рис. 1.6 Эволюция вектора намагниченности