А ктивное сопротивление в цепи переменного тока

Рисунок 2.5 - Резистор в цепи переменного тока

На рисунке 2.5 показана простейшая цепь с резисто-ром, подключённым к синусоидальному напряжению.

U_R(t) = U_msin (ωt+ψ_u) = i(t) R

i_R(t) = U_m/R sin (ωt+ψ_u) = I_msin (ωt+ψ_i)

ψ_u = ψ_i

I_m=U_m/R или, для действующих значений, I = U/R – закон Ома.

В комплексной форме закон Ома: Ú = İ Z

В данном случае - Z = R , Ú = İ R

Комплексное сопротивление в этой цепи является чисто действительным числом, мнимая часть сопротивле-ния равна нулю – Х = 0 и R называется активным сопротивлением.

Угол φ = ψ_u-ψ_i – называется сдвигом фаз между током и напряжением.

В цепи с активным сопротивлением R сдвиг фаз между током и напряжением равен нулю:

φ = 0, ψ_u = ψ_i

Вектора тока и напряжения совпадают по направлению. Совпадают также формы тока и напряжения.

Катушка индуктивности в цепи переменного тока

Зависимость между током и напряжением в катушке индуктивности L (рисунок 2.6) выражается формулой:

Пусть через катушку течёт ток:

i_L(t) = I_m sin (ωt + ψ_i)

Тогда напряжение на катушке:

u_L(t) = LI_mω cos (ωt + ψ_i) = ωLI_msin (ωt + ψ_i+π/2) =

= U_mLsin (ωt + ψ_u)

где U_mL= ωLI_m

ψ_u= ψ_i+ π/2

Таким образом, ток в катушке отстаёт от напряжения на ней на 90⁰ (рисунок 2.7).

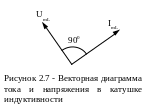
Коэффициент пропорциональности между током и напряжением имеет размерность сопротивления и называется: индуктивным сопротивлением.

X_L = U_mL/I_mL = U_L/I_L = ωL

X_L всегда положительно

Для постоянного тока ω = 0 => X_L = 0

При постоянном напряжении, катушка представляет собой просто провод, сопротивлением которого мы дого-ворились пренебрегать, хотя в реальности его активное сопротивление R, хоть и мало, но не равно нулю.

Важное замечание: индуктивное сопротивление X_L имеет смысл только для синусоидального тока и равно отношению действительных либо амплитудных, но никак не мгновенных значений!

Х_L ≠ u_L(t) / i_L(t)

Конденсатор в цепи переменного тока

Пусть к конденсатору приложено напряжение u(t) (рисунок 2.8):

u_c(t) = U_m sin (ωt + ψ_u)

Ток через конденсатор:

Если напряжение постоянно, то ток через конденсатор равен нулю. Для переменного тока:

i_C(t) = C U_mω cos (ωt + ψ_u) = ωCU_m sin (ωt +ψ_u+ π/2) = = I_m sin (ωt + ψ_i)

Амплитуда тока: I_m = ω C U_m

Начальная фаза тока: ψ_i= ψ_u+ π/2

Таким образом, ток в конденсаторе опережает напряжение на нём на 90⁰ (рисунок 2.9).

Коэффициент пропорциональности между током и напряжением имеет размерность сопротивления и называет-ся: ёмкостное сопротивление.

X_С = U_mС/I_mС = U_С/I_С = 1/ωC

X_С всегда положительно

Для постоянного тока ω = 0 => X_С = ∞

При постоянном напряжении, конденсатор предста-вляет собой бесконечное сопротивление – разрыв в цепи.

Так же, как и в катушке индуктивности: ёмкостное сопротивление X_С имеет смысл только для синусоидального тока и равно отношению действительных либо амплитудных, а не мгновенных значений.

Х_С ≠ u_С(t) / i_С(t)

В конденсаторе и катушке комплексное сопротивление является чисто мнимым числом, действительная часть (активное сопротивление) равна нулю – R = 0.