Глава 4 Мощность в цепи переменного тока Мощность в цепи с активным сопротивлением

Поскольку ветви, содержащие один элемент – R, L или C – были детально рассмотрены, в этом разделе не будут вновь приводиться рисунки 2.4, 2.5, 2.7.

Мгновенная мощность:

p(t)=u(t) i(t) = U_m sin (ωt+ψ_u) I_m sin (ωt+ψ_i)

В цепи с активным сопротивлением ψ_u= ψ_i, поэтому:

p(t) = U_mI_m sin²(ωt+ψ_i)

Из тригонометрии известно, что sin²α = (1- cos2α)/2. Тогда:

Г рафик p(t) показан на рисунке 2.24.

Среднее значение косинуса равно нулю, следовательно, среднее значение мгновенной мощности (постоянная составляющая):

Мощность Р называется активной мощностью и измеряется в Ваттах и также является синусоидой, но с частотой 2ω – в два раза большей, чем у тока и напряжения. Она всегда положительна (если не равна нулю), направление потока энергии всегда направлено в одну сторону – от источника энергии к нагрузке.

Активное сопротивление всегда потребляет мощность, откуда и следует его название.

Мощность в цепи с реактивным сопротивлением

Соотношения для цепей с катушкой индуктивности или конденсатором во многом схожи. Рассмотрим мгновенную мощность в ветви с катушкой L.

p (t) = u (t) i (t) = U_m sin (ωt+ψ_u) I_m sin (ωt+ψ_i) =

= U_m sin (ωt+ψ_i+π/2) I_m sin (ωt+ψ_i) =

= U_m cos (ωt+ψ_i) I_m sin (ωt+ψ_i)

С реднее значение мгновенной мощности равно нулю (рисунок 2.25). Коэффициент при синусе называется индуктивной мощностью Q_L.

U_L = I X_L => Q_L= I²ωL = U²/ωL

Половину периода при p(t)>0 катушка является приёмником энергии – потребляет мощность (знаки напряжения и тока совпадают), а вторую половину при p(t)<0, за счёт запасённой энергии магнитного поля, является источником энергии (знаки напряжения и тока противоположны).

П рименив аналогичные выводы формул для цепи с конденсатором С, получим аналогичные результаты.

(здесь разница: ψ_u вместо ψ_i в цепи с катушкой)

Далее – всё аналогично. Среднее значение мгновен-ной мощности равно нулю (рисунок 2.26). Коэффициент при синусе называется ёмкостной мощностью Q_С.

I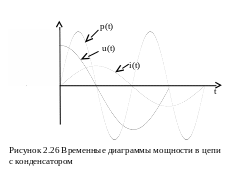 _C = U X_C => Q_C= U²ωC = I²/ωC

Половину периода при p(t)>0 конденсатор является приёмником энергии – потребляет мощность (знаки напряжения и тока совпадают), а вторую половину при p(t)<0, за счёт запасённой энергии электрического поля, является источником энергии (знаки напряжения и тока противоположны).

Временные диаграммы у катушки и конденсатора несколько отличаются, но основные положения идентичны.

Полная мощность. Треугольник мощностей

Сделаем некоторые выводы.

Существует два типа элементов: активные элементы, всегда только потребляющие мощность и реактивные, средняя мощность потребления у которых равна нулю.

При синусоидальных напряжениях и токах все мгновенные мощности также являются синусоидальными функциями, частота их при этом в два раза больше, чем у тока и напряжения.

Активная мощность Р измеряется в Ваттах – Вт.

Реактивная мощность Q измеряется в варах (Вольт-Ампер реактивный, ВАр).

Q = Q_L- Q_C.

Полная мощность S измеряется в Вольт-Амперах (ВА).

‌‌S = P + jQ =

Для записи комплекса мощности через ток и напряжение, необходимо использовать понятие комплексно сопряжённого числа.

Д ля тока – İ = I₁ + jI₂ = I e^jψi

Комплексно сопряжённый ток: = I₁ - jI₂ = I e^-jψi

Комплекс мощности:

S = Ù

S = U e^jψu I e^-jψi = U I e^{j(ψu - ψi)} = S e^jφ

Основные соотношения такие же, как для сопротивлений.

φ = arctg Q/P P = S cos φ Q = S sin φ

Для наглядности можно это представить в виде треугольника мощностей, который подобен треугольнику сопротивлений, с таким же углом φ (рисунок 2.27).

Важную роль в промышленном потреблении энергии играет угол сдвига фаз φ. Большинство потребителей энергии имеют индуктивный характер нагрузки (электродвигатели и пр.), в связи с чем увеличивается cos φ. Увеличение реактивной мощности за счёт активной означает бесполезное расходование мощности электрогенераторов и, зачастую, огромные материальные затраты – например при работе крупных промышленных предприятий.

Для предотвращения этого, на предприятиях, параллельно основной, подключается дополнительная ёмкостная нагрузка – для компенсации. Косинус φ должен соответствовать определённым нормам и не превосходить 0,9 - 0,95.