§ 3. Диаграммы Венна

У же можно было заметить некоторые специфические свойства операций над множествами, в особенности то свойство, что одно и то же множество может быть определено различными путями. Далее в этой главе мы обсудим способы доказательства этих свойств формальным путём, однако часто полезно иметь геометрические представления множеств. Такие представления не могут заменить доказательства, но могут быть полезны, чтобы быстро и просто убедиться, справедливо ли конкретное утверждение и, следовательно, доказательство его возможно или же оно неверно. В этом случае можно заметить, как следует строить пример, чтобы доказать, что оно неверно. Диаграммы, которые мы будем использовать, называют диаграммами Венна (по имени английского математика Джона Венна) и строят, как это описано ниже.

Во-первых, начертим большой прямоугольник, пред­ставляющий ξ (рис. 1.1). Во-вторых, начертим круги (или какие-либо другие подходящие замкнутые кривые) внутри прямоугольника, чтобы представить множества. Они должны пересекаться в наиболее общем случае, тре­буемом в задаче, и должны быть соответствующим обра­зом обозначены (рис. 1.2). Точки, которые лежат внутри различных областей диаграммы, сейчас могут рассматри­ваться как элементы соответствующих множеств. Если число элементов во множествах мало, тогда отдельные эле­менты могут быть записаны внутри подходящих обла­стей, как это показано в примере 3.1.

П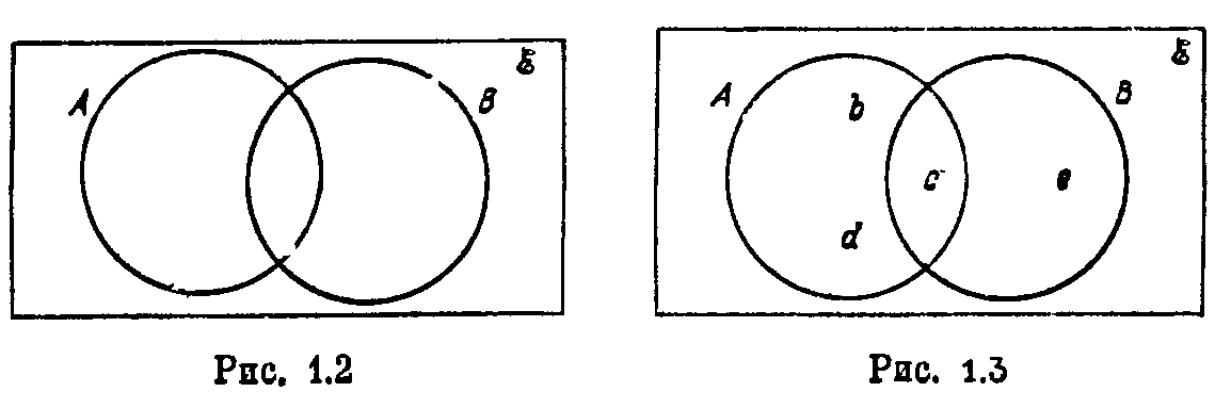 ример 3.1. Пусть ξ = {b, c, d, e}, A = {b, c, d}, B = {c, e}. Соответствующая диаграмма изображена на рис. 1.3. Этот рисунок полностью иллюстрирует при­мер 3.1, обеспечивая знание элементов ξ. Если же, например, A ξ , тогда неясно, что предполагалось изобразить на диаграмме. В тех случаях, когда используются более сложные конструкции множеств, следует избегать изображения их в виде диаграмм.

Имея построенную подходящим образом диаграмму, мы можем заштриховать определенные области для обо­значения вновь образованных множеств.

Пример 3.2. Чтобы представить множество A (В' С), начнем с общей диаграммы, показанной на рис. 1.4. Заштрихуем В' диагональными линиями в од­ном направлении, а С диагональными линиями в другом направлении (рис. 1.5).

П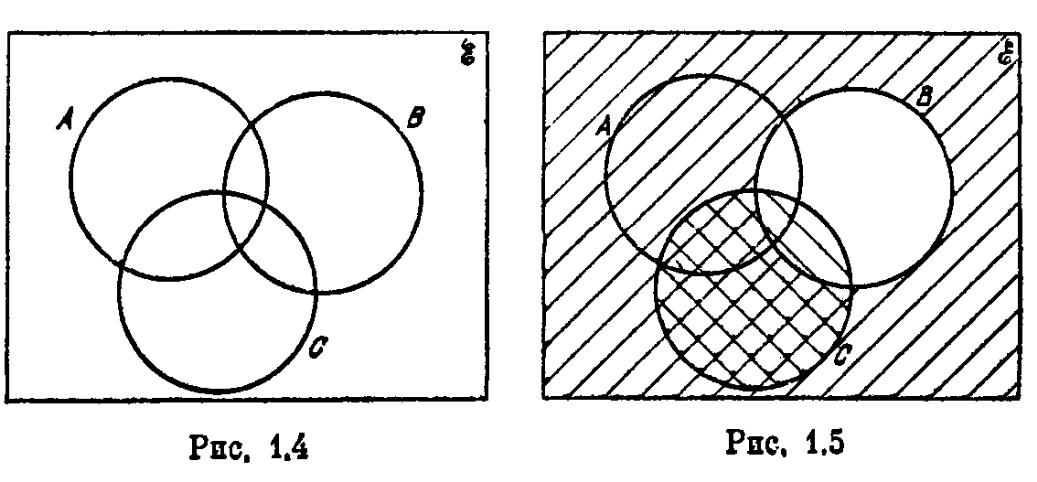 лощадь с двойной штриховкой представляет собой множество В' С.

На новой копии диаграммы заштрихуем эту область горизонтальными линиями, а А вертикальными. Вся за­штрихованная на рис. 1.6 область представляет множе­ство A (В' С). Если в отдельных случаях мы имеем дополнительную информацию о рассматриваемых мно­жествах, то ее можно использовать для упрощения диа­граммы Венна.

Пример 3.3. Пусть А В = 0; это соответствует диаграмме на рис. 1.7. //

З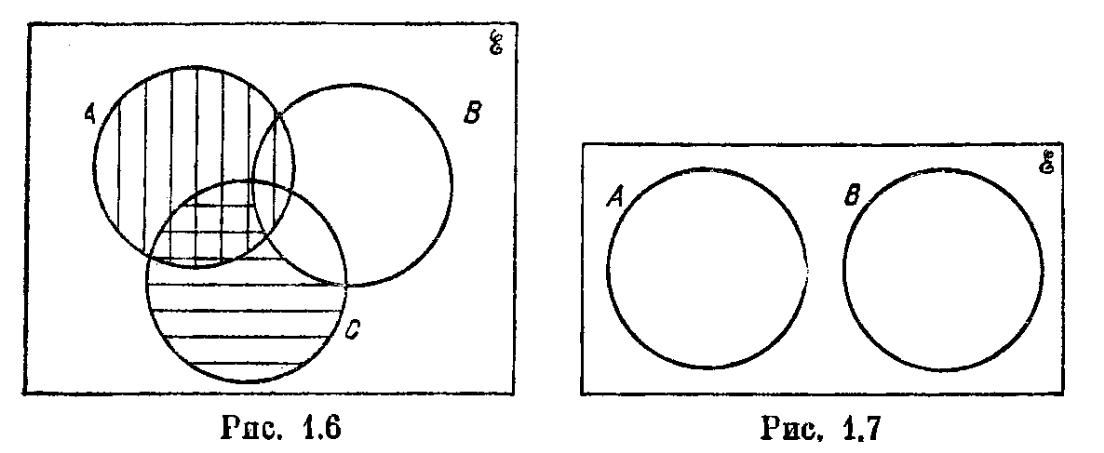 аметим, что в большинстве случаев множества содержат довольно много элементов, и, следовательно, эти элементы не могут быть представлены отдельно. Поэтому более удобно в этом случае говорить о каждом из множеств как о целом и не упоминать отдельных элементов.

Упражнение 1.3.

1. Начертить диаграмму, иллюстрирующую построе­ние множеств, рассматриваемых в задаче 1 упражне­ния 1.2.

2. Как можно представить следующие множества, ис­пользуя диаграммы Венна:

{A, {A}}, {{a}, {b}}, {X, Y, Z}, где

X = {x: x=1 или (x-2) X},

Y = {x: x=3 или (x-3) Y},

Z = {x: x=2 или (x-2) }?