§ 5. Аналитические свойства вещественных функций

Этот параграф содержит материал, использующий теорию множеств из гл. 1. Цель, которая при этом пре­следуется, состоит не в развитии техники вычислений, а в создании строгих утверждений типа:

«Предел f(x) при х, стремящемся к 0, есть y»,

«Наклон графика f в точке а равен b»,

«f имеет гладкий график» и т. п. (Два последних понятия, очевидно, относятся к графи­ке.) Мы дадим основные определения, которые исполь­зуются при получении некоторых результатов. Этого до­статочно для того, чтобы проиллюстрировать доказатель­ства большинства теорем.

5.1. Последовательности. Вещественной последова­тельностью называется отображение N на R. Последова­тельность записывают в виде (а_n). Если при возраста­нии п члены а_n становятся «близкими» к некоторому фиксированному значению 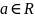, то говорят, что после­довательность (a_n) имеет предел а или что 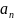стремится к а при стремлении п к бесконечности. Дадим строгое определение сказанному.

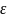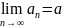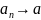Определение. Если (а_n) — вещественная последо­вательность и для любого > 0 существует та­кое, что . , то говорят, что (a_n) имеет предел а, и записывают это как или при (Здесь |х| обозначает модуль числа .)

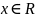Если (a_n) имеет предел, то говорят, что последова­тельность сходится. Если последовательность не имеет предела, то говорят, что она расходится.

Пример 5.1.

1. Последовательность (а_n), где а_n = 1/n, имеет пре­дел 0; для > 0 можно выбрать 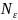. — любое натураль­ное число, большее 1/ . Тогда

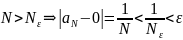
следовательно,

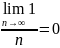
2. Последовательность (а_n), где 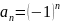, расхо­дящаяся.

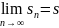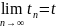Предложение. Если (S_n) и (t_n)— последователь­ности и , тогда (s_n + t_n), (s_nt_n) и ( s_n) также яв­ляются последовательностями, и если и , mo:

а)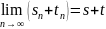

б)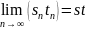

в)

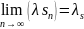
г) если 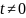, то при .

Доказательство. Пусть . Тогда существует такое, что

и

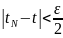
при . Так как при

то . Аналогично для случая б)

.

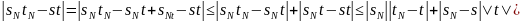Пусть задано . Тогда существует такое, что для справедливы неравенства

,

.

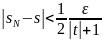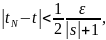
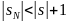Следовательно,

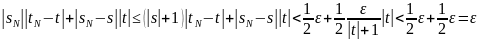
Откуда получаем 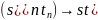. Доказательство случаев в), г) предложения оставляем в качестве упражнения.

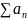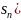Определение. Пусть (a_n) – последовательность в R. Последовательность определяет ряд . При этом называют n-й частичной суммой ряда. Если последовательность ( сходится, то говорят, что ряд сходящийся, и число 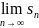называют суммой ряда. Оно обозначается

.//

5.2. Непрерывность. Понятие непрерывности почти полностью игнорируется при изучении элементарных вычислений. В неформальной математике это понятие считается очевидным. Однако при начальном изучении ма­тематики достаточно трудно найти нужный путь. На са­мом деле определение непрерывности базируется на по­нятии предела. В этом параграфе через I будем обозна­чать интервал действительной оси R. Если 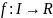становится «неограниченно близким» к некоторому числу b при х, «приближающемся» к 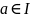, то говорят, что предел f(x) при х, стремящемся к а, есть b. Дадим строгое определение этого понятия.

Определение. Функция f: 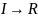имеет предел b в точке а, если для любого ε > 0 существует δ_ε > 0 та­кое, что

.

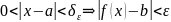В этом случае будем писать

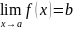
или

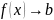при . //

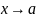Заметим, что в определение не входит значение f(х) в точке а.

Пример 5.2.

1. ; достаточно выбрать

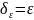
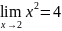2. , поскольку

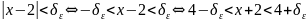
Следовательно,

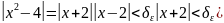
Если выбрать 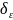= min(1, ε/5), то

.//

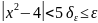Легко показать эквивалентность следующих утвер­ждений:

, ,

, .

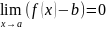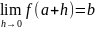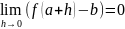Теперь мы готовы к изучению понятия непрерывно­сти для вещественных функций. Грубо говоря, функция непрерывна в точке , если точки, «близ­кие» к а, отображаются в точки, «близкие» к f(а), Бо­лее строго это понятие может быть определено следую­щим образом.

Определение. Функция непрерывна в , если

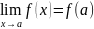
Говорят, что f(x) непрерывна, если она непрерывна в каждой точке своей области определения. //

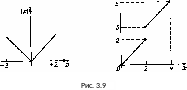
Из определения видно, что в данном случае требует­ся, чтобы f(x) была определена при х = а. Такое опре­деление непрерывности соответствует интуитивному представлению. Поясним его на рисунках.

На рис. 3.9, а дан график непрерывной 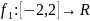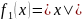функции , .На рис. 3.9, б представлен гра­фик функции , где

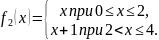
Функция f2 непрерывна в каждой точке [0, 4], за исклю­чением точки х = 2, так как не существует интервала вида 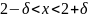, для которого .

В заключение этого раздела сформулируем без дока­зательства несколько утверждений. Их доказательство можно найти в большинстве книг по математическому анализу. Если и при , то

,

,

при условии

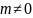
для всех .

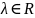Отсюда следует, что если f и g непрерывны в точке а, то непрерывными являются и функции λf, f + g, fg, f/g при условии, что а находится в области определения каждой из «новых» функций.

5.3. Дифференцируемость. Графическое представле­ние функции 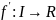, обсуждаемое в п. 5.2, предполага­ло, что эта функция определяет некоторую другую функ­цию , где f'(а) есть «наклон» графика f в точ­ке а. В общем случае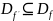 , так как на самом деле его может не быть для всех точек 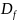. В этом случае f' не существует. Определим строго функцию f’.

Определение. Функция дифференцируе­ма в точке , если

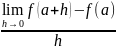
существует. Множество точек, где этот предел существу­ет, устанавливает область определения производной функции f, и

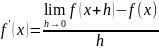
Иногда производную f' записывают как df/dx. Отноше­ние 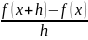часто записывают в виде δf/δx, где δ читают как «малое приращение». В этих обозначениях

.//

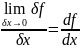Если f дифференцируема в точке а, то она и непре­рывна в a, так как

;

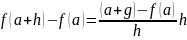следовательно,

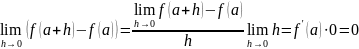
Другими словами, , и, таким образом, f непрерывна в а по определению. Поэтому непрерыв­ность функции является необходимым условием ее дифференцируемости, но не достаточным, как показывает следующий пример.

Пример 5.3. Функция f(x)=|x| не дифференцируема в точке х = 0, так как

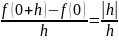
где

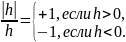
Следовательно, в любом интервале ] -h, h[, где h произ­вольное, функция |h|/h принимает оба значения ±1, и поэтому предел при h → 0 по существует. //

Пример 5.4.

1. Пусть f: R → R — постоянная функция, т. е. f(х) = с для всех . Тогда

и 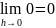. Таким образом, f’(х)= 0 для всех . Обратно, если f'(x)=0 для всех , тогда f—посто­янная.

2. Пусть f(x)= х² для всех . Тогда

,

.

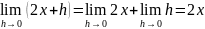Следовательно, f'(х) = 2х для всех . //

Предложение. Если f дифференцируема в х и λϵR, то λf дифференцируема в х и

.

Доказательство.

. //

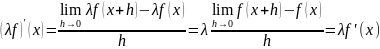Следующие результаты оказываются полезными при дифференцировании функций, которые определены че­рез другие функции.

Предложение. Если fugдифференцируемы в х,

то

а) f + g дифференцируема в х и

;

б) fg дифференцируема в х и

;

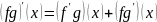в) fig дифференцируема в х при g(x)≠ 0 и

.

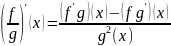Доказательство оставляем в качестве упражнения.

Эти формулы могут использоваться при доказатель­стве некоторых, возможно, знакомых простых резуль­татов.

Пример 5.5.

1. Пусть f: R → R, где f(x)= 1/х. Тогда

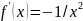и .

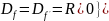2. Пусть f: R → R задано формулой f(x) = xⁿ (nϵN). Тогда f'(x)=nx^n-1. //

П р е д л о ж е н и е (правило дифференцирования слож­ной функции). Если f дифференцируема в х и g диффе­ренцируема в y = f(x), то g ° f дифференцируема в х и

.

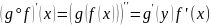Доказательство. Пусть ω = g(y)= g(f(x)) = gºf(x). Тогда 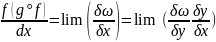(при условии δy≠0)= (см. п. 5.1). Однако f дифференцируема в точке х, поэтому

;

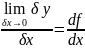аналогично

.

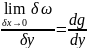Поэтому

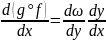и . //

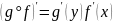Производную от f' записывают в виде f" или d²f/dx² и называют второй производной функции f. Аналогично производная от (n≥3) записывается как f⁽ⁿ⁾

или dⁿf/dxⁿ и называется n-й производной функции f. Если f' существует и непрерывна, то говорят, что f при­надлежит классу С¹; f^. принадлежит классу Cⁿ, если f⁽ⁿ⁾ существует и непрерывна, и классу С^∞, если f⁽ⁿ⁾ суще­ствует для всех п ϵ N.

5.4. Интегрирование. Пусть f: [a, b] → R, nϵN, h=(b-a)/n и x_h=a+kh при 0 ≤ k < n. Тогда можпо определить последовательность (s_n(f)):

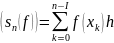
Если (s_n(f)) имеет предел, то будем говорить, что f интегрируема на [а, b], и обозначать

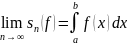
Величину называют интегралом Римана функции f(x) на [a, b].

З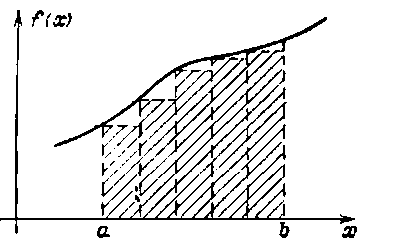 аштрихованная площадь на рис. 3.10 является гра­фическим представлением s₅(f) для непрерывной функ­ции f на [а, b]. Для неограниченно больших значений интуитивно можно ожидать, что заштрихованная пло­щадь будет хорошо аппро­ксимировать площадь под графиком между х = а и х = b и ограниченным зна­чением (если оно существу­ет) этой площади. Если обозначает мно­жество всех вещественных функций на [а, b], то интег­рирование может рассматриваться как функция 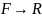, область определения которой есть

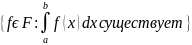
Некоторые важные свойства интеграла приводятся ниже.

Предложение.

а) Если f непрерывна на [а, b], то она интегрируема на этом отрезке;

б) если f интегрируема на [а, b] и x ϵ [а, b], тогда f интегрируема на [а, х] и [х, b] и

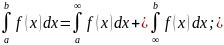
в) если f интегрируема на [а, b] и λ ϵ R, тогда λf интегрируема на [а, b] и

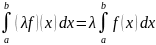
г) если fug интегрируемы на [а, b], то f + g интегрируема на [а, b] и

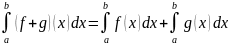
Доказательство. В случае а) формальное дока­зательство давать не будем. Заметим, однако, что для непрерывной функции f интуитивно ясно, что площадь под графиком f является хорошо определенным поняти­ем, и, следовательно, можно ожидать, что интеграл от f существует. Доказательства б) — г) следуют из соответ­ствующих свойств последовательностей. Рассмотрим, на­пример, случай г). Если fug интегрируемы па [а, b], то последовательности

имеют пределы. Рассмотрим последовательность s_n(f) + + s_n (g). Тогда

Чтобы вычислить интеграл, редко используют опреде­ление и вычисляют предел. Следующая теорема является основной. (Она устанавливает тот факт, что интегрирова­ние и дифференцирование — взаимно обратные процессы.)

Теорема. Пусть 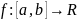непрерывна. Опреде­лим функцию формулой

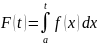
Тогда F дифференцируема на [а, b] и F' = f.

Доказательство. Будем лишь фиксировать ос­новные моменты доказательства. Используя результаты предыдущего предложения, имеем

Рассмотрим

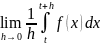
Из определения интеграла и его интерпретации как площади ясно, что для малых h интеграл стремится к f(t)h и

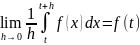
Следовательно,

F’(t) = f(t) для всех tϵ[a,b]. //

Пусть Ф — произвольная функция, для которой Ф' =f. Тогда F — Ф является постоянной, так как

F’(t)=f(t)=Ф’(t)

Следовательно,

(F — Ф)' (t)=0 для всех t ϵ [а, b],

и из п. 5.3 заключаем, что F — Ф = λ, λϵ R. Таким образом,

Функцию Ф называют неопределенным интегралом от f и обозначают 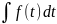. Неопределенный интеграл опре­делен с точностью до постоянного слагаемого. Он опре­деляет класс эквивалентности функций [Ф]: Ф₁~Ф₂ тогда и только тогда, когда Ф1 и Ф2 — неопределенные интегралы от f.

Предложение. Если Ф — неопределенный интег­рал от f, то

Доказательство.

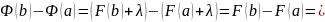
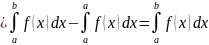
Как и при исследовании дифференцирования, эти результаты могут быть использованы для вычисления интегралов, некоторые примеры которых даны ниже.

Пример 5.6.

1. Если 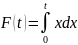, то F'(t) = t, и неопределенные

интегралы от функции f: х→ х есть

Ф(t)=t²/2+λ, λϵR

Таким образом,

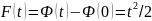
2. В более общем случае, если f: х→ хⁿ для п ϵ Z\{—1} и 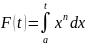, то F’(t)=tⁿ, и неопределенный интеграл есть

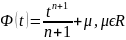
Тогда

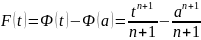
Очевидно, что это соотношение неверно при п = —1. Этот случай будет рассмотрен в п. 5.5.

5.5. Некоторые специальные функции. Мы предпо­лагаем, что читатель знаком с геометрическими опреде­лениями функций sin х и cos х, из которых следует, что

sin: R → [—1, 1], cos: R → [— 1, 1],

где

Мы также предполагаем знакомство с периодическими свойствами этих функций. Некоторые другие элементар­ные свойства приведены в следующем предложении. Предложение. Для всех х, у ϵ R имеем:

а)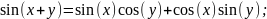

б)

в)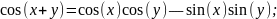 r)

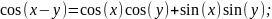
д)sin² x + cos² x = 1;

е) . //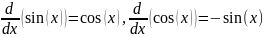

Эти результаты непосредственно следуют из опреде­лений. Их доказательство оставляем читателю в качест­ве упражнения. Мы не будем касаться обоснования этих понятий (можно принять их в качестве допущений).

В п. 5.4 был определен 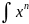при п ≠ — 1. В действительности интеграл 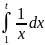существует для всех t>0 и равен In t. Функцпя ln является отображением ]0, ∞[ → R и обладает свойством

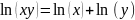для всех х, у ϵ ]0, ∞[,

так как

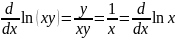
Из результатов п. 5.4 имеем ln(xy) — ln х = λ, где хϵ]0,∞[ и λϵR. В частности, при х = 1 имеем ln у — In 1 = λ и ln 1=0; поэтому lnу=λ. Следовательно,

ln(xy) = In х + In у.

Можно показать, что ln биективна и, следовательно, су­ществует функция

exp: R → ]0,∞[

такая, что ln {exp р} = р для всех рϵ R и exp {ln q} = q для всех qϵ]0,∞ [. Из свойств функции ln следует, что

ерх{х + у} = exp x exp y для всех х, yϵR,

exp 0 = 1,

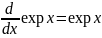
Удобно обозначить ln х через log_e х, a exp х через е^x.

Функцию log_eх называют натуральным логарифмом числа х, а функцию х→е^х — экспоненциальной функ­цией.

Если при а > 0 функция f: ]—а, а[ → R принадлежит С^∞ и xϵ]-a,a[,то ряд

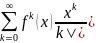
называют рядом Маклорена для f в точке х. Для неко­торых функций можно показать, что ряд Маклорена схо­дится к значению функции f в точке х. Другими слова­ми, для f имеем

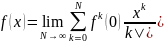
В частности, это справедливо для функций sin x, cos x, е^х, для которых

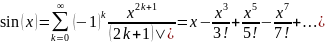
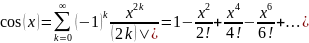
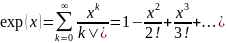
для всех xϵR

Упражнение 3.5.

1. Показать, что последовательности, определенные ниже, сходятся, и найти их пределы:

а) s_n= 1/n²;

б) s_n=3n/(n + 3);

в) s_n = 1 + 1/2ⁿ.

2. Пусть (s_n) и (t_n)—последовательности,

и n |t_n |< |s_n| для всех n ϵ N. Показать, что

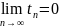
3. Доказать, что если (s_n) и (t_n) имеют пределы s и t соответственно, то последовательность (р_n), где р_п =λs_n, имеет предел λs. Если t ≠ 0, то

4. Найти производные следующих функций (опреде­лить области, в которых существует производная):

a)

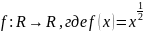
б)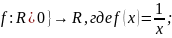

в)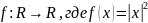

5. Показать, что если fug дифференцируемы в точ­ке х, то:

а) f + g дифференцируема в точке х и

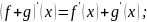
б) fg дифференцируема в точке хи

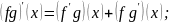
в) f/g дифференцируема в точке х при g(x)≠ 0 и

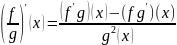
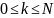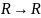5. Показать, что если a_kϵR при и определено соотношением

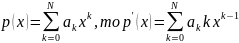
7. Определить производные следующих функций:

а) f: R→ R, где f(х) = х sin х/(1 + cos х),

б) g: R → R, где g (х) = sin х² + х cos² х.

8. Вычислить интегралы:

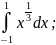a) б) в)

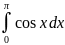
9. Найти неопределенные интегралы:

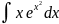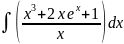a) б) в)