§ 3. Кольца и поля

По-видимому, простые операционные структуры § 2 не были знакомы читателю. Сейчас мы готовы исполь­зовать свойства групп для описания арифметических структур, обсуждавшихся 'в гл. 4. Наибольший интерес для нас представляют поля (на текущий момент это наи­более идеальные арифметические структуры) и их клас­сификация в терминах размерности, Однако сначала мы

140 кратко рассмотрим структуры, которые несколько отли­чаются от полей и называются кольцами.

3.1. Кольца. Многие математические конструкции, ко­торые естественно возникают в линейной алгебре (осо­бенно в теории матриц), являются кольцами пли вклю­чают кольца как подструктуры. Следовательно, примеры колец часто будут появляться в этой главе и в гл. 6. Мы уже изучили одну совокупность колец. Вернемся к ней после введения аксиоматических понятий.

Определение. Кольцом называется множество R с двумя определенными на нем бинарными операциями и такими, что:

а) ассоциативна;

б) ассоциативна;

в) коммутативна;

г) имеет единицу, которая называется нулем и обо­значается 0;

д) существуют обратные элементы относительно ;

е) дистрибутивна по отношению к , т. е.

х (у z) = (х у) (х z), (х у) z = (х z) (у z) для всех x,y,z R. //

Следовательно, система (Z_n, *, +) при любом n N является кольцом.

Будем говорить, что кольцо коммутативно, если ум­ножение коммутативно, и является кольцом с едини­цей, если существует единица относительно умножения. Как обычно, ее обозначают символом 1. Легко показать, что в кольце (R, , ) для любых a, b R выполня­ются соотношения

0 а = а 0 = 0,

а (–b) = (–а) b = – (а b), (–а) (–b) = а b.

Здесь –а это элемент, обратный к а относительно ; а (–b) записывают обычно как а – b, и если 1 R, то 1 единственна.

Пример 3.1. (Z_n, *, +) является коммутативным кольцом с единицей при любом n е N. /

В системе (Z_n, *, +) не всегда возможно «деление». В этом состоит основное отличие между полем и комму­тативным кольцом с единицей. Рассмотрим кольцо (Z₆, *, +). Покажем, что оно не является полем,

В Z₆ существует 15 случаев, когда произведение двух элементов может давать нуль, а именно:

(0, 0),

(0, 1), (0, 2), (0, 3), (0, 4), (0, 5),

(1,0), (2, 0), (3, 0), (4, 0), (5, 0),

(2, 3), (3, 4),

(3, 2), (4, 3).

Очевидно, что существуют утверждения, которые спра­ведливы не для всех арифметических вычислений. При умножении выражений мы явно используем тот факт, что а * b = 0 тогда и только тогда, когда а = 0 или b = 0.

В кольце (R, , ) нулевые элементы хну назы­вают делителями нуля, если их произведение равно ну­лю. В случае, когда R не является коммутативным коль­цом, х называют левым делителем нуля, а у — правым делителем нуля. Нетрудно показать (см. упражнение 5.3), что Z₆ имеет делители нуля (так как 6 — составное число) и что Z_p не имеет делителей нуля тогда и только тогда, когда р является простым числом.

Если в группе (G, )

а b = а с,

то b = с. Однако в случае произвольного кольца это не­верно.

Теорема. Приведенное выше условие имеет место в кольце R тогда и только тогда, когда R не содержит делителей нуля.

Доказательство. Достаточность. Предпо­ложим, что R не имеет делителей нуля. Тогда, если х у = х z ш х = 0, то

(х у) – (х z) = (х у) – (х у) = 0,

(х у) – (х z) = (х у) (х (– z)) =

= (x {у (–z)) = х (у – z).

Поэтому x (y – z) = 0; но так как не существует де­лителей нуля и х 0, то отсюда следует, что y – z = 0 и, следовательно, y – z. Аналогично, если у х = z х, то y = z. Достаточность доказана.

Необходимость. Предположим, что из а b = а с следует равенство b = с, и пусть х у = 0. Тогда

x y = x 0

(см. упражнение 5.3), и если х 0, то у = 0. Аналогично, если у 0, то

x y = 0 = 0 у

и по предположению х = 0. Таким образом, из х у = 0 следует, что или х = 0, или у = 0. //

Рассмотрим теперь еще одну структуру, перед тем как перейти к изучению полей

Определение. Областью целостности называется коммутативное кольцо с единицей, не имеющее делите­лей нуля, т. е. множество D с двумя бинарными опера­циями и такими, что:

а) сложение ассоциативно;

б) сложение коммутативно;

в) существует единица по сложению, обозначаемая 0;

г) существуют обратные элементы по сложению (обо­значаются (—х));

д) умножение ассоциативно;

е) умножение коммутативно;

ж) существует единица по умножению (обознача­ется 1);

з) умножение дистрибутивно по отношению к сло­жению:

(х (у z)) (х у) (х z) для всех x,y,z<= D;

и) если х 0 и х у = х z, то у = z. //

Каждая конечная область целостности является по­лем, однако существуют примеры бесконечных областей целостности, не являющихся полями.

3.2. Поля. Уже работая с понятиями арифметики, мы сталкивались с аксиоматическим определением поля.

Определение. Полем называется множество F с двумя определенными на нем бинарными операциями — сложением и умножением (обозначается (F, , ) или же просто F), которые удовлетворяют следующим девяти свойствам.

1. Сложение коммутативно:

х у — у х для всех х, y F.

2. Сложение ассоциативно:

х (у z) = (х у) z для всех х, у, z F.

3. Существует элемент в F, который обычно обозна­чается символом 0, такой, что

х 0 = х для всех х F;

0 называется аддитивной единицей или просто нулем,

4. Каждому элементу соответствует элемент y F такой, что

x у = 0;

у называется аддитивным обратным элементом к х и обозначается через –х.

5. Умножение коммутативно:

х у = у х для всех x, y F,

6. Умножение ассоциативно:

x (y z) = (x y) z для всех x,y,z F.

7. Существует элемент в F, который обычно обозна­чается символом 1, такой, что 1 0 и

х 1 = х для всех x F

1 называют мультипликативной единицей или просто единицей.

8. Каждому элементу х F \{0} соответствует элемент y F такой, что

х у = 1;

у называется мультипликативным обратным элементом к х и обозначается через х^-1.

9. Умножение дистрибутивно относительно сложения:

х (у z) = (x у) (х z) для всех x,y,z F. //

Пример 3.2. (R, *, +) является полем, и, следова­тельно, (R, +) и (R\{0}, *) — коммутативные группы. (N, *, +) не является полем, поскольку не существует ни аддитивной единицы, ни аддитивных обратных эле­ментов. (ρ(A), , ) для заданного множества А не яв­ляется полем, поскольку не существует обратных эле­ментов. //

В предыдущем определении использовались символы и для того, чтобы подчеркнуть, что операции в по­ле могут отличаться от умножения и сложения. Однако в дальнейшем часто будут рассматриваться поля (R, *, + ) и (Q, *, +), Поэтому мы будем использовать сим­волы * и +.

Перед тем как перейти к доказательству основных утверждений, напомним (вместе с доказательствами) не­которые важные следствия, которые непосредственно из­влекаются из определения поля.

Предложение. Единичный элемент в поле един­ствен.

Доказательство. Предположим, что

х*е = х и х*е' = х для всех x F,

Тогда

е = е * е' = е' * е = е'

Поэтому е = е' = 1.

Для операции сложения доказательство аналогично. // Предложение. Обратные элементы в поле единственны.

Доказательство. Опять рассмотрим случай опе­рации умножения. Возьмем х F\{0} и допустим, что имеется два элемента у и z таких, что

х * у = 1, х * z = 1.

Из коммутативности следует, что

y * x = 1 = z * x;

поэтому

у = у * 1 = у * (х * z) = (у * х) * z = 1 * z = 1.

Следовательно, у = z = x^-1.

Единственность обратных элементов по сложению до­казывается аналогично. И

Перейдем к основным результатам. Теорема. В поле (F, *,+) для любых a, b F справедливы следующие утверждения:

а) а * 0 = 0;

б) (–а) = а*(–1), –а(+b) = (–а) + (–b);

в) –(–а) = а, (–1).( –1)–1;

г) если а * 0, то (а–¹)^-1 = а;

д) а * b = 0 а = 0 или b = 0;

е) (–а) * (–b) = а * b.

Доказательство.

а) а * 1 = а и а + 0 = а; поэтому

а + (а * 0) = (а * 1) + (а * 0) = а * (1 + 0) = а * 1 = а.

Следовательно, а * 0 является единицей по сложению. Она единственна; поэтому а * 0 = 0.

б) Аналогично

а + (а *(–1)) = (а * 1) + (а * (–1)) = а * (1 + (–1)) = а * 0 = 0.

Таким образом, –а = а*(–1). Используя это равенство, получаем

– (а + b) = (а + b)*(–1) = (а*(–1)) + (b*(–1))=(–а) + (–b).

в) По определению

(–а)+ а = 0 и (–а) + (– (–а)) = 0.

Но обратные элементы единственны; поэтому а = – (–а). Таким образом, 1 = – (–1), Пусть х равно –1. Тогда

1 = – (х) = х * (–1) = (–1)*( –1).

г) Заметим вначале, что а^-1 0, так как в противном случае

1 = а * а^-1 = а * 0 = 0,

что противоречит свойствам поля. Следовательно, а^-1 0 и доказательство аналогично доказательству случая в).

д) Возьмем а 0. Тогда а^-1 определено и

b = 1 * b = (а^-1 * a)* b = а^-1 *(а * b)= а^-1 * 0 = 0.

е) Из случая б) следует

(– а) = а *(– 1) и (– b) = b * (– 1),

Поэтому

(– а) * (– b) = (а * (–1)) * (b *(–1) ) =

= а*((–1)*( –1))* b = а * 1 * b = а * b. //

Для упрощения записи выражений в полях примем обычное соглашение о том, что если нет скобок, то ум­ножение выполняется раньше сложения. Например, вы­ражение а + b * с означает а + (b * с).

Из аксиом поля следует разрешимость линейных уравнений. Это — очень важное свойство, и можно при­вести аргументы в пользу того, что оно — основное свой­ство полей.

Линейным уравнением относительно х над полем F называется выражение вида а * x + b = 0, где 0, а, b F.

Теорема. Если а 0, то линейное уравнение а * х + b = 0 имеет единственное решение в F (т. е. су­ществует только один элемент поля, при подстановке ко­торого в уравнение получается верное равенство).

Поле F замкнуто относительно заданных операций. По­этому элемент (–b) * а^-1 содержится в F. Этот элемент и дает решение уравнения. Более того, так как обрат­ные элементы в F единственны, то –b и а^-1 определя­ются из данного уравнения единственным образом, и, следовательно, решение единственно. И

Уравнения, которые получаются из полиномов более высоких степеней, например квадратные уравнения

а * х * х + b * х + с = 0

с коэффициентами а, b, с из R, в общем случае нераз­решимы в R. Для того чтобы эти уравнения были разре­шимы, нужно перейти к расширению поля R — полю комплексных чисел. Однако полиномиальные уравнения с комплексными коэффициентами всегда разрешимы в поле комплексных чисел: никакого более широкого поля не требуется. Исследование этого интересного факта мог­ло бы увести нас в сторону от более уместных тем.

3.3. Конечные поля. До сих пор все упоминаемые по­ля были бесконечны (содержали множества, имеющие мощность 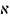₀ или ₁). Обсудим теперь возможность суще­ствования конечных полей — полей, содержащих конеч­ное число элементов. Сформулируем основные свойства конечных полей и докажем некоторые из них (доказа­тельства других лежат за пределами этой книги). Внача­ле приведем некоторую дополнительную информацию.

Пусть a F. Тогда элементы а, а + а, а + а + а, .,. являются элементами поля. Обозначим их через а, 2а, За, ,,., па, .,, (не требуется, чтобы n F) соответствен­но. Аналогично а, а * а, а * а * а, ... также являются элементами поля. Обозначим их через а, а², а³, ..., а", ... соответственно. Предположим, что а 0.

Определение. Если существует целое n N та­кое, что па = 0 (и не существует меньшего целого r N такого, что rа = 0), то п называют аддитивным порядком а. Если существует m N такое, что a^m = 1 (и не су­ществует меньшего r N такого, что а' = 1), то т назы­вают мультипликативным порядком а. //

Теорема. Ненулевые элементы поля F имеют один и тот же аддитивный порядок.

Доказательство. Возьмем а, b F\{0} и пред­положим, что аддитивные порядки а и b равны п и т соответственно. Тогда

nb = п(а * а^-1) * b =(nа) * (а^-1 * b) = 0 * а^-1 * b = 0. Поэтому m n. Аналогично

та = m(b * b ^-1)* а = (mb) * (b ^-1 * а) = 0 * b ^-1* а = 0.

Следовательно, п т, и поэтому т = п. //

Определение. Если в поле F все ненулевые эле­менты имеют аддитивный порядок п, то говорят, что F имеет характеристику п. Если такого аддитивного поряд­ка не существует, то говорят, что поле имеет характери­стику, равную 0. //

Если |F| = m N, т. е. F имеет m элементов, то гово­рят, что F конечно. Если F имеет характеристику, рав­ную 0, то оно должно быть бесконечным. (См. упражне­ние 5.3.)

Теорема. Характеристика любого конечного поля является простым числом.

Доказательство. Предположим, что конечное по­ле F имеет характеристику п и n = р * q, где р, q < n и р, q N, Возьмем

а F\{0}.

Тогда 0 = na = (p*q)a = p(qa). Далее qa F. Поэтому, если qa = 0, выполняется соотношение п q (поскольку порядок а равен п); в противном случае qa F\{0}, по­рядок qa также равен п и поэтому п р. Таким обра­зом, в обоих случаях получаем противоречие. Следова­тельно, таких р и q не существует и п простое. //

Таким образом, мы получили следующий основной результат.

Теорема. Конечное поле имеет характеристику р (простое число) и |F| = р^п для некоторого n N,

Доказательство. Мы уже знаем, что F имеет характеристику р, причем р простое. Пусть |F| = q. Если р = q, то утверждение теоремы очевидно. В противном случае возьмем элемент а₁ F\{0} и положим

Φ₁ = {y: y = na₁; n N, 1 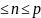}, | Φ₁| = р.

Рассмотрим теперь элемент a₂ F\Φ₁,и пусть

Φ₂ = {y: y = na₁+ ma₂; n N, 1 , 1 }.

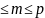Если Φ₂ = F, то процесс заканчивается; в противном слу­чае рассмотрим а₃ F\Φ₂ и т. д. В конце концов (посколь­ку F конечно) процесс остановится и мы получим совокуп­ность множеств Φ₁, Φ₂ ,..., Φ_n для некоторого n N.

Каждый элемент из F единственным образом пред­ставим в виде

= m₁a₁ + m₂a₂ + ... + m_na_n,

причем 1 < m_i < р для всех i = 1, ..., n. (Доказать это в качестве упражнения.) Следовательно, существует р^п таких выражений, и, таким образом, |F| = рⁿ. //

Итак, любое конечное поле должно иметь р^п элемен­тов при некоторых р, n N (р простое). На самом деле для любых таких p и n существует поле порядка р^п, однако доказать это не совсем просто.

Рассмотрим в качестве примера поле (Z3, *, +), где * и + определены в табл. 5.1. Нетрудно показать, что выполнены условия 1—8 из определения поля.

Таблица 5.1

*	0	1	2			+	0	1	2
0	0	0	0			0	0	1	2
1	0	1	2			1	1	2	0
2	0	2	1			2	2	0	1

Для контраста рассмотрим соответствующую табл. 5.2 Для Z₄

Таблица 5.2

•	0	1	2	3			+	0	1	2	3
0	0	0	0	0			0	0	1	2	3
1	0	1	2	3			1	1	2	3	0
2	0	2	0	2			2	2	3	0	1
3	0	3	2	1			3	3	0	1	2

Очевидно, что не существует мультипликативного об­ратного элемента к 2. Поэтому Z₄ с естественной опера­цией умножения не является полем. Поле порядка 4 = 2² хотя и существует, но не совпадает с Z₄ (см. уп­ражнение 5.3). Конечные поля заданного порядка стро­ятся достаточно сложным образом — на основе теории многочленов над другими структурами (не полями). Они имеют важное значение в теории кодирования. Мы не будем этим заниматься, поскольку такое приложение яв­ляется довольно специальным.

3.4. Упорядоченные поля. Мы уже видели, что мно­жество R вместе с обычными операциями сложения и умножения определяет поле. Однако структура поля са­ма по себе не дает какого-либо упорядочения элементов, которое мы обычно связываем с R. Не все поля могут быть упорядочены. Поэтому мы должны проверить, ка­кие дополнительные условия должны быть выполнены, прежде чем рассматривать это понятие. Обычные свой­ства порядка можно получить, как и ожидается, многими способами. Начнем с определения свойства положитель­ности. Оно непосредственно приводит к отношению по­рядка в поле, а затем к понятию длины. Основные ре­зультаты этого параграфа будут сформулированы в двух теоремах, а вспомогательные результаты даны в виде упражнений.

Определение. Говорят, что поле F упорядочено, если оно содержит непустое подмножество Р, которое замкнуто относительно операций сложения и умножения, и такое, что для каждого элемента х из F имеет место ровно одно из соотношений

x Р\{0}, x = 0, Р\{0}.

Р есть множество всех положительных элементов F. (На этом этапе отметим, что 0 может как включаться в Р, так и не включаться. Для определенности выберем слу­чай, когда 0 включается в Р, что согласуется с изложе­нием предыдущей части книги.)

Если х Р, то будем говорить, что элемент х поло­жителен, и обозначать этот факт как х 0. Если –х Р\{0}, то будем говорить, что элемент х отрицателен, и обозначать это как х < 0. Аналогично, если х и у – элементы F, то будем говорить, что х меньше или равно у (обозначается х у), тогда и только тогда, когда у – х Р, и что х меньше у (х<у), тогда и только тогда когда у – х Р \ {0}. Символы <, можно также использовать для записи в противоположную сторону. //

Из этих определений можно получить, что « » явля­ется отношением порядка и выполняются все ожидае­мые свойства.

Теорема. Пусть F — упорядоченное поле и а, b, с, d F. Тогда:

а) если а b и b с, то а с;

б) а а;

в) если a b и b а, то а =b

г) если а 0, то а² 0;

д) 1 > 0;

е) если а b, то а + с b + с;

ж) если а b и с d, то а + с b + d;

з) если а b, 0 с и d 0, то а * с b * с, b * а * d;

и) если 0 < а, то 0 < а^-1, и если b < 0, то b^-1< 0,

Доказательство.

а) а b и b c (b – a) Р по определению (с – b) Р Тогда c – a = с – b + b –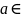 Р, поскольку Р замкнуто относительно сложения. Следовательно, а с.

б) Очевидно, что а – а = 0 Р.

в) а b и b a; поэтому если b – а = х, то 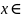Р и 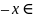Р, что противоречит определению Р. Поэтому х = 0 и а = b.

г) Если а 0, то или а Р, или –а Р Поскольку /> замкнуто относительно умножения, то а Р a² Р и, как показано в п. 3.2,

(–а) * (–а) = а², откуда – а Р a² Р,

д) 1² = 1, поэтому из случая г) следует, что 1 > 0.

е) Утверждение непосредственно следует из соотно­шения

b – а = (b + с) – (а + с).

ж) Требуемый результат получаем из соотношения

(b – a) + (d – c) = (b + d) – (a + c), используя замкнутость Р.

з) Утверждение доказывается аналогично, используя следующие соотношения:

(b – а)*с – b*с – а*с (b – a)* (b – a )*(–d) = а * d – b * d.

Оставшаяся часть доказательства проводится анало­гично. //

Получим похожие соотношения для понятия величи­ны в упорядоченных полях.

Определение. Если F — упорядоченное поле, то абсолютным значением (величиной, длиной или модулем) называется функция

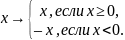
Традиционно эту функцию обозначают как |х| (х – ар­гумент) и читают это как «модуль х». //

Сформулируем без доказательств основные результа­ты, относящиеся к функции |х|. (Доказательства остав­ляем в качестве упражнения.)

Теорема. Если F — упорядоченное поле и а, b F, то:

а) |а| = 0 тогда и только тогда, когда а = 0;

б) |–a| = |а|;

в) |а * b| = |а| * |b|;

г) если 0 b, то |а| b тогда и только тогда, когда –b a b;

д) – |а| а |а|;

е) ||а| – |b|| |а 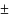b| |а| + |b| (неравенство тре­угольника). //

Упражнение 5.3.

1. Доказать, что в кольце (R, *, +) выполняются со­отношения:

а) 0 * а = а * 0 = 0;

б) а * (–b) = (–a) * b = – (а * b);

в

в) (–а) * (–b)= а * b.

2. Показать, что если в кольце (R, *, +) для каждо­го а R выполняется соотношение а * а = а, то R ком­мутативно.

3. Показать, что в кольце Z_n, делителями нуля явля­ются только те элементы, которые имеют общие нетри­виальные множители с п. Следовательно, Z_P, где р про­стое, не имеет делителей нуля.

4. Показать, что каждая конечная область целостно­сти является полем.

5. Показать, что (Z, *, +) – область целостности, но не поле.

6. Пусть p < q и (Z_P, *_P, +_P) и (Z_P, *_P, +_P) – обыч­ные системы по модулю р и q. Доказать, что, хотя они и являются коммутативными кольцами и Z_p Z, кольцо (Z_P, *_P, +_P) не является подкольцом (Z_q, *_q, +_q,). Пока­зать, что операции *, и +, не замкнуты на Z_P.

7. Без использования теорем доказать, что (Z₆, *, +) не является полем (* и + суть операции по модулю 6).

8. Доказать, что конечное поле имеет ненулевую ха­рактеристику и что поле с характеристикой 0 бесконечно.

9. Пусть a₁, a₂, ..., a_n определены так же, как и при доказательстве последней теоремы п. 3.3. Доказать, что любое выражение вида

m₁a₁ + m₂a₂ + ... + m_na_n

определяет некоторый элемент поля, причем такое пред­ставление единственно.

2. В поле (F, *, +) с операциями, определенными ниже, решить систему линейных уравнений

х + d * у = с,

х * d + у = b,

*	а	b	с	d			+	а	Ь	с	d
а	а	а	а	а			а	а	b	с	d
b	а	b	с	d			b	b	а	d	с
с	а	с	d	b			с	с	d	а	b
d	а	d	b	с			d	d	с	b	а

2. Доказать, что если а * b > 0, a, b F, то пли а, b > 0, или a, b < 0.

3. Доказать, что в упорядоченном поле а²+b² = 0 тогда и только тогда, когда а = b = 0.

4. Пусть F — упорядоченное поле и a, b е F такие, что 0 а b. Доказать, что a² b².

5. Доказать, что каждое поле является областью це­лостности.

6. В упорядоченном поле, складывая неравенства

–|а| а |а| и –|а| – a |а|,

доказать, что:

а) |а ± b| |a| + |b|;

б) ||a| – |b|| |а ± b|.