
- •Предисловие
- •Введение
- •Глава 1. Множества
- •§ 1. Множества н их спецификация
- •§ 2. Простейшие операции над множествами
- •X ∉ ø при любом х.
- •§ 3. Диаграммы Венна
- •§ 4. Подмножества и доказательства
- •§ 5. Произведения множеств
- •Глава 2. Отношения
- •§ 1. Основные понятия
- •§ 2. Графические представления
- •§ 3. Свойства отношений
- •§ 4. Разбиения и отношения эквивалентности
- •§ 5. Отношения порядка
- •§ 6. Отношения на базах данных и структурах данных
- •§ 7. Составные отношения
- •§ 8. Замыкание отношений
- •Глава 3. Функции
- •§ 1. Функции и отображения
- •§ 2. Обратные функции и отображения
- •§ 3. Мощность множеств и счетность
- •§ 4. Некоторые специальные классы функций
- •§ 5. Аналитические свойства вещественных функций
- •§ 6. Операции
- •Глава 4. Основные понятия арифметики
- •§ 1. «Малая» конечная арифметика
- •§ 2. «Большая» конечная арифметика
- •§ 3. Двоичная арифметика
- •§ 4. Логическая арифметика
- •Глава 5. Алгебраические структуры
- •§ 1. Алгебраические структуры и подструктуры
- •§ 2. Простейшие операционные структуры
- •§ 3. Кольца и поля
- •§ 4. Линейная алгебра
- •4.1. Векторные пространства о линейные преобразования.
- •§ 5. Решетка и булевы алгебры
- •§ 6. Замкнутые полукольца
- •Глава 6. Матрицы
- •§ 1. Матрицы и бинарные отношения на конечных множествах
- •§ 2. Матрицы над другими алгебраическими структурами
- •§ 3. Матрицы и векторные пространства
- •Глава 7. Теория графов
- •§ 1. Вводные понятия
- •§ 2. Маршруты, циклы и связанность.
- •§ 3. Планарные графы
- •3.1. Теоремы Эйлера и Куратовского.
- •3.2. Раскраска карт и графов.
- •§ 4. Структуры данных для представления графа
- •§ 5. Обход графа
- •5.2. Обход графа по глубине.
- •5.4. Остовные леса обходов по глубине и ширине.
- •§ 6. Ориентированные графы
- •6.2. Маршруты и связность в орграфах.
- •Глава 8. Языки и грамматики
- •§ 1. Основные понятия
- •§ 2. Грамматики с фразовой структурой
- •2.1. Основные определения.
- •§ 3. Контекстно-свободные языки
- •§ 4. Понятия грамматического разбора и грамматических модификаций
- •§ 5. Грамматики операторного предшествования
- •Глава 9. Конечные автоматы
- •§ 1. Общие понятия
- •§ 2. Конечные автоматы
- •§ 3. Регулярная алгебра
- •Глава 10.Компьютерная геометрия
- •§ 1. Системы координат для подмножеств r3
- •§ 2. Преобразования
- •§ 3. Кривые и поверхности
§ 4. Линейная алгебра
В большинстве элементарных учебников векторы определяют как объекты, обладающие «величиной» и «направлением». Такой подход берет начало из приложений в геометрии и физике. Эти вопросы формально будут обсуждаться в п. 4.2. Дадим более общее определение вектора, для которого понятия величины и направления несущественны.
4.1. Векторные пространства о линейные преобразования.
Определение. Пусть F — поле, а V — множество с бинарной операцией +. Предположим, что для каждого а F и х V определен элемент ах V, Тогда, если выполнены аксиомы:
а) (V, +) —коммутативная группа;
б) для всех х, у
F
и a,
b
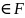
(а + b)х = ах+ bх,
a(х + у) = ах + ау,
(ab)x = а(bх),
1Fx = x,
где 1F — мультипликативная единица в F, то говорят, что V является векторным пространством над F, Элементы V называются векторами, операция + называется сложением векторов, а отображение
Λ: F X V → V,
определяемое соотношением Λ (а, х) = ах, называют умножением вектора на скаляр. //
Векторное пространство над F может рассматриваться как тройка (V, +, Λ), удовлетворяющая приведенным выше аксиомам. Нуль векторного пространства по сложению обозначают символом 0. Из аксиом следует, что
0Fx = 0 для всех x V,
где 0F — аддитивная единица в F, и
а0 = 0 для всех а F.
В следующих примерах будет показано, что различные классы множеств обладают структурой векторного пространства.
Пример 4.1.
Fn (n N) является векторным пространном над F с операциями
(a1, ..., an) + (b1, ..., bn) = (a1 + b1, ..., an + bn),
a(a1, ..., an) = (aa1 ..., aan).
Нулем Fn является вектор (0F, ..., 0F). Элементы a1, ... , an называются компонентами вектора а = (a1, ..., ап).
Пусть Φ — множество всех отображений f: [а, b] → R. Тогда Φ является векторным пространством над R с операциями
(f + g)(x) = f(x)+g(x) для всех f, g Φ,
Пусть ζ, ζ ⊂ Φ — множество всех непрерывных отображений из Φ. Тогда ζ является векторным пространством с операциями, определенными в Φ. //
Множество U, U ⊆ V, называется векторным подпространством пространства V, если оно является векторным пространством с операциями из V.
Множество {(a1,
..., аn-1,
0F):
ai
F}
является векторным подпространством
пространства Fn;
ζ является векторным
подпространством пространства
Φ.
Если U,
U
⊆
V,— векторное
подпространство пространства V,
то 0
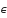 U.
U.
Векторные пространства Rn (1 n 4) возникнут естественным образом в гл. 10. Операции в Rn имеют геометрическую интерпретацию. Для пространства R2 это показано на рис. 5.3. Если r = (x, y) ∊ R2, то компоненты х и у измеряются вдоль ортогональных линий, начиная с точки пересечения О (рис. 5.3, а). Компоненты х и у откладываются вдоль линий ОХ (ось х) и OY (ось у) соответственно. Эти линии проведены под углом 90° друг к другу, и угол между ними измеряется против часовой стрелки от оси ОХ. Такую систему осей называют правосторонней системой координат в R2. Векторное сложение в R2 геометрически соответствует правилу параллелограмма, как это показано на рис. 5.3, с.
Геометрия векторных пространств Rn будет рассматриваться ниже, а сейчас мы введем понятия базиса и
Р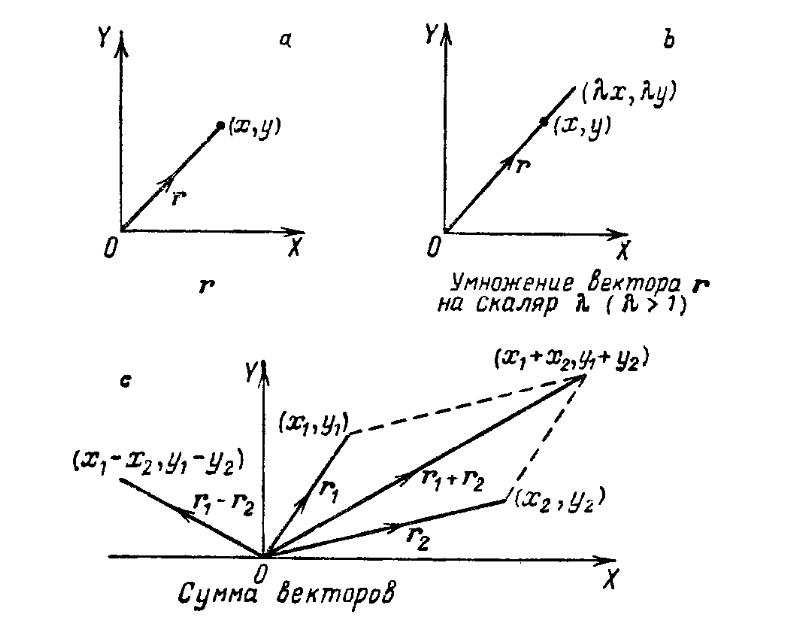 ис.
5.3
ис.
5.3
размерности. Если V — векторное пространство над F и S s V, то сумму вида
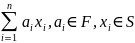
называют линейной комбинацией векторов из S. Говорят, что конечное множество векторов {хi: 1 i k} является линейно независимым, если
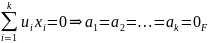
в противном случае множество является линейно зависимым. Подмножество S ⊆ V такое, что любой элемент V представим в виде линейной комбинации элементов из S, называется порождающим множеством пространства V (или же еще говорят, что S порождает V), Упорядоченное линейно независимое порождающее множество пространства V называется базисом этого пространства.
Пример
4.2. В R3
вектор (5, 5,
 )
является линейной комбинацией
векторов (1, 1, 0) и (0, 0, 3), так как
)
является линейной комбинацией
векторов (1, 1, 0) и (0, 0, 3), так как
(5,5,
)
= 5(1,1,0)+
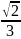 (0,
0,3).
(0,
0,3).
Множество L = {(1, 1, 0), (0, 0, 3)} является линейно независимым подмножеством в R3, так как а(1, 1, 0) + b(0, 0, 3) = (а, а, 3b) = 0 тогда и только тогда, когда а = 0 и b = 0. Однако подмножество L не является базисом, поскольку оно только определяет векторное подпространство
{(x, х, у): x, y ∊ R} ⊂ R3.
Базис B = L {(1, 0, 0)} «расширяет» L до базиса в R3. //
Легко показать, что каждый элемент векторного пространства имеет единственное представление в фиксированном базисе, так как если V имеет базис В = {e1,..., en} и
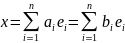
то
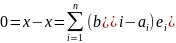
Однако В — линейно независимое множество. Поэтому bi = аi для всех i, 1 I п.
Докажем следующий важный результат.
Предложение. Пусть S = {х1 ..., хт) — порождающее множество пространства V, a L= {y1, ..., уn) — линейно независимое множество векторов из V, Тогда т > 1.
Доказательство. Предположим, что т < 1. Так как S порождает V, то существуют элементы а1, ..., am ∊ F такие, что
y1 = a1x1 + ... + атхт.
Однако y1
0, так как L
— линейно независимое множество
(см. упражнение 5.4), и, следовательно, не
все а1,
..., ат
равны нулю. Для определенности положим
а1
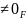 .
Тогда
.
Тогда

т. е. x1 является линейной комбинацией {y1, х2, ..., хm}. Так как S порождает V, то по доказанному выше множество векторов {у1 x2, ..., хm} также порождает V. Аналогично получаем, что {y1, у2, хз, ..., хm) порождает V. Повторяя этот процесс т раз, получаем, что множество {y1, ..., ym} порождает V. Следовательно,

где pi, ..., pm^F не все равны нулю (так как ym+i не может быть равно нулю). Отсюда

однако последнее невозможно, потому что {y1, ..., уn} — линейно независимое множество векторов. Следовательно, m > l. //
Предложение. Пусть В и В' — базисы векторного пространства V над F. Тогда |В| — |В'|.
Доказательство.
Пусть B
= {e1,
..., еn}
и В'
= {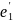 ,...,
,...,
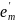 }.
Тогда из предыдущего предложения
следует, что n
m
и m
п, т. е.
m
= п. //
}.
Тогда из предыдущего предложения
следует, что n
m
и m
п, т. е.
m
= п. //
Мощность базиса векторного пространства V называется размерностью V и обозначается через dim(V).
Предложение. dim(Fn) = n.
Доказательство. Определим В = {е1,..., еn}, г
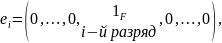
и покажем, что В является базисом в Fn, Очевидно, что

поэтому В порождает Fn и

Следовательно, В является базисом в Fn и dim(V) = |В| = п. //
Из данного выше определения следует, что базис всегда состоит из конечного числа векторов, и не во всяких векторных пространствах можно выделить базис (например, нет Φ, ζ базиса), Понятия базиса и размерности можно расширить на все векторные пространства, однако такое обобщение нам не потребуется. Если пространство V имеет базис, соответствующий данному выше определению, то говорят, что пространство имеет конечную размерность, а само пространство называется конечномерным векторным пространством.
Рассмотрим теперь гомоморфные отображения между векторными пространствами.
Определение. Пусть V1 и V2 — векторные пространства над полем F. Говорят, что отображение Т: V1 → V2 линейно, если
T (x + y) = Tx + Ty, T(ax) = a(Tx).
Если V1 = V2, то Т называют линейным преобразованием пространства V1. //
Далее нас будут интересовать конечномерные векторные пространства над R и линейные преобразования над ними. В оставшейся части главы через V будем обозначать векторное пространство, а через End(V)—множество всех линейных преобразований V (эндоморфизмов V). Заметим, что большинство приводимых утверждений можно представить в более общем виде.
Перейдем от алгебры V к алгебре End(V) и покажем, что End(V) замкнуто по отношению к естественным операциям сложения, умножения и умножения на скаляр. Вначале заметим, что единичное отображение Iv и нулевое отображение 0V являются линейными на V, так как по определению
Iv х = х для всех x ∊ V,
0vх = 0 для всех х ∊ V,
Следовательно, для всех х, у ∊ V и λ ∊ R имеем
Iv (х + у) = x + у = Ivx + Ivy,
Iv (λ х) = λ х = λ(Iv x),
0v(х + у) = 0 = 0 + 0 = 0vx+ 0v у,
0v (λх) = 0 = М) = λ 0vх.
Если S,
T
∊
End(V),
то сумма S
+ Т и
произведение S T
(композиция) определяются
формулами
T
(композиция) определяются
формулами
(S+T)x = Sx + Tx для всех x ∊ V
(S Т)х = S(Tx) для всех х ∊ V.
Отметим следующие свойства End(V) относительно приведенных выше операций.
Предложение. Множество (End(V), , +) является кольцом с единицей.
Доказательство. Укажем основные этапы доказательства. Надо показать, что:
S, Т ∊ End(V) ⇒ S+T ∊ End (V) и S Т ∊ End (V);
(End(V), +) – коммутативная группа.
Если S, Т, U ∊ End (V), то:
S (T U) = (S T) U;
S (T+U) = S T + S U;
Iv T = T Iv = T. Имеем
(S + T)(х + у)=S(х + у)+T(х + у)= Sх + Sу + Tх + Tу =(Sх + Tх) + (Sу + Tу) = (S + T)х+(S + T) у.
Аналогично (S + T) (λ х) = S λ x + Т λ х = λ Sх + λ Tx =
= λ (Sx + Tх) = λ (S + T)х.
Доказательство того, что S Т ∊ End (V), оставляем в качестве упражнения.
(S + (T+U))x = Sx + (T+U)x = Sx + (Tx+Ux) = (Sx + Tx)+Ux = (S + T)x+Ux = ((S + T)+U)x.
Следовательно, операция + ассоциативна. Элемент 0V ∊ End (V) удовлетворяет условию
T + 0v = 0v + T = T для всех T ∊ End(V)
и является аддитивной единицей End (V). Для T ∊ End(V) определим отображение –T: V → V соотношением
(–T)х = – (Tх) для всех х ∊ V.
Легко показать, что –T ∊ End (V) и
(–T + T)= T + (–T) = 0v.
Поэтому отображение –T является аддитивным, обратным к T. Коммутативность (End(V), +) следует из коммутативности (V, +).
Утверждение следует из результатов гл, 3.
Для х ∊ V имеем
(S (T + U))x = S((T + U)x)=S(Tx + Ux)= =S(Tx)+S(Ux) = (S T)x + (S U)x =
= (S T + S U)x.
Утверждение очевидно. //
Пусть T ∊ End (V) и λ ∊ R, Определим отображение λT: V → V следующим образом:
(λT)х = λ(Tх) для всех x ∊ V. Легко показать, что λT ∊ End(V). Отображение
Λ: R × End(V) → End(V),
определяемое соотношением Λ (λ, Т) = λТ, называют умножением на скаляр.
Предложение. (End(V), +, Λ) — векторное пространство над R.
Доказательство. Из предыдущего утверждения следует, что (End(V), +) — коммутативная группа; следовательно, нам надо показать, что умножение на скаляр удовлетворяет условиям
(λ + ) T = λ T + T, λ(S + T) = λS + λT,
(λ )T = λ( T), 1RT=T,
где λ, ∊ R и S, Т ∊ End (V). Имеем цепочку соотношений
((λ + )T)х = ( λ + ) (Тх) = λ (Tх) + (Tх) = (λT)х + ( T)х.
Остальные соотношения доказываются аналогично. //
Предложение. Операции умножения в кольце и умножения на скаляр Λ в End(V) удовлетворяют соотношению
λ(S T) = (λ S) T = S (λ T), где λ ∊ R и S, T ∊ End(V).
Доказательство. ((λ (S T))х = λ ((S Т)х) = λ (S(Tх)) = (λ S)(Tх) = ((λS) T)х,
(λ (S T))х = λ ((S T)х) = λ (S(Tх))=»
= S(λ (Tх)) = (S (λT))х. //
Алгебраические структуры, удовлетворяющие таким же свойствам, как и End (V), называют линейными алгебрами. Дадим строгое определение.
Определение. Четверка (X, +, , Λ) называется линейной алгеброй над R, если Λ: R X × X → X и
(X, +, Λ)—векторное пространство над R;
(X, +)— кольцо;
Λ и удовлетворяют условиям
λ(x1«х2) = (λх1) х2 = x1 (λх2)
для всех λ ∊ R и x1, х2 ∊ X. //
Результаты, полученные для End (V), можно сформулировать следующим образом.
П р е д л о ж е н и е. End (V) с введенными выше операциями является линейной алгеброй с мультипликативной единицей. //
Если T ∊ End(V) и существует преобразование S: V → V такое, что
S T = T S = IV,
то (см. упражнение 5.4) S ∊ End(V). Тогда Т называют обратимым, a S = Т-1 — обратным к Т преобразованием. Обозначим через Aut(V) множество всех обратимых преобразований из End (V), т. е. множество автоморфизмов V.
П р е д л о ж е п и е. (Aut(V), ) является группой.
Доказательство.
Так как IV
∊
Aut(V)
и IV
IV
= IV,
следовательно, существует
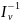 ,
равное IV.
Пусть S
∊
Aut(V);
тогда
,
равное IV.
Пусть S
∊
Aut(V);
тогда
S-1 S = S S-1= IV
Поэтому (S-1) -1 существует и совпадает с S. Следовательно, S-1 ∊ Aut(V). Если теперь S, T ∊ Aut(V), то
(S Т) (T-1 S-1) = S (T T-1) S-1 = S S-1 = IV.
Аналогично
(T-1 S-1) (S T) = IV
Поэтому (S Т) -1 существует, и из S, T ∊ Aut(V) следует, что S Т ∊ Aut(V). Ассоциативность операции уже доказана. //
 .2.
Структурные изображения в Rn.
Рассмотрим геометрическую интерпретацию
пространства Rn,
при которой понятия «направление»
и «величина» для векторов имеют
геометрический смысл. Вернемся к
геометрическому изображению R2.
Мы видим, что если r
= (х, у) ∊
R2,
то расстояние от точки (х, у) до (0, 0) есть
(х2
+ у2)1/2.
Обозначим это расстояние через ||r||,
которое можно рассматривать как
отображение ||r||:
R2
→ R.
Оно называется длиной,
модулем или нормой.
Рассмотрим точки r1
= (x1,
у1)
и r2
= (х2,
y2)
.2.
Структурные изображения в Rn.
Рассмотрим геометрическую интерпретацию
пространства Rn,
при которой понятия «направление»
и «величина» для векторов имеют
геометрический смысл. Вернемся к
геометрическому изображению R2.
Мы видим, что если r
= (х, у) ∊
R2,
то расстояние от точки (х, у) до (0, 0) есть
(х2
+ у2)1/2.
Обозначим это расстояние через ||r||,
которое можно рассматривать как
отображение ||r||:
R2
→ R.
Оно называется длиной,
модулем или нормой.
Рассмотрим точки r1
= (x1,
у1)
и r2
= (х2,
y2)
Рис. 5.4
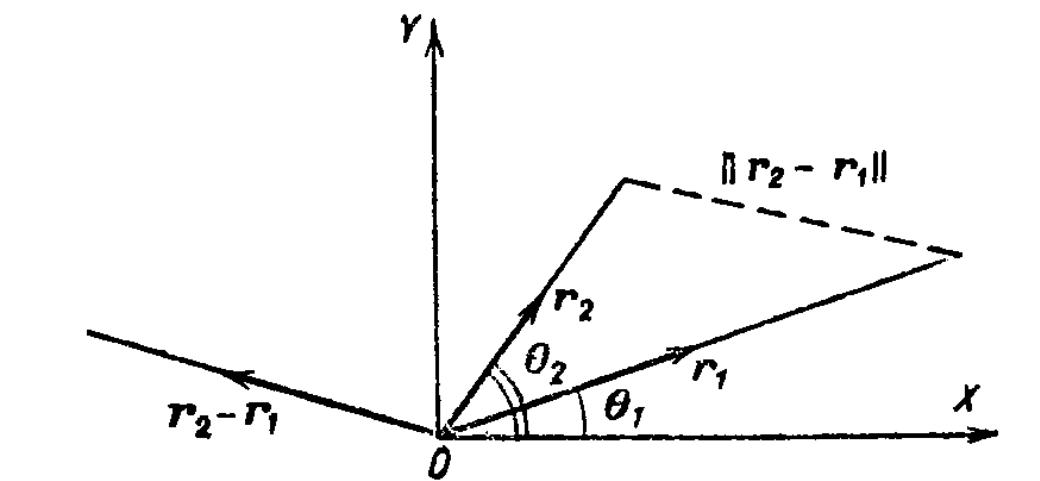
(рис. 5.4). Пусть θ1 и θ2 — углы в интервале [0, π] между положительной полуосью ОХ и векторами r1 и r2 соответственно. Тогда расстояние между r1 и r2 равно ||r1 – r2||, а угол между ними равен θ = θ2 – θ1 Имеем
cos θ = cos (θ 2 – θ 1) = cos θ1 cos θ2 + sin θ1 sin θ2 =
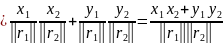
Выражение
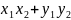 можно использовать для вычисления
расстояний и углов в R2.
Определим отображение
можно использовать для вычисления
расстояний и углов в R2.
Определим отображение
Ф: R2 × R2→R
следующим образом:
Ф(r1 и r2) =
Тогда
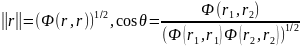
Угол
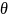 между двумя векторами в R2
определяется однозначно при условии,
что
< 0 < π. Когда
= 0 или
= π, то говорят, что r1
и r2
параллельны (коллинеарны). В
прикладной математике удобно обозначать
между двумя векторами в R2
определяется однозначно при условии,
что
< 0 < π. Когда
= 0 или
= π, то говорят, что r1
и r2
параллельны (коллинеарны). В
прикладной математике удобно обозначать
 через r1
•
r2
и называть
скалярным произведением
r1
и r2.
Если r1
0
и r2
0,
то r1
•
r2
= 0 тогда и только
тогда, когда
= π/2; в этом случае говорят, что r1
и r2
взаимно ортогональны,
перпендикулярны
или нормальны.
Ниже приведены некоторые свойства
скалярного произведения.
через r1
•
r2
и называть
скалярным произведением
r1
и r2.
Если r1
0
и r2
0,
то r1
•
r2
= 0 тогда и только
тогда, когда
= π/2; в этом случае говорят, что r1
и r2
взаимно ортогональны,
перпендикулярны
или нормальны.
Ниже приведены некоторые свойства
скалярного произведения.
Предложение.
а) r • r ≥ 0 и r • r = 0 тогда и только тогда, когда r = (0, 0);
б) r1 • r2 = r2 • r1 для всех r1 , r2 ∊ R2;
в) r1 • (r2 + r3) = r1 • r2 + r1 • r3 для всех r1, r2, r3 ∊ R2;
г) λ (r1 • r2) = (λ r1) r2 = r1 • (λ r2), r1, r2 ∊ R2, λ ∊ R2
Доказательство.
а) Если r = (x, y) ∊ R2, то r • r = (x2+y2) ≥ 0 для всех х, y ∊ R2 и г • г = О тогда и только тогда, когда x = 0 и y = 0.
б) r1 • r2 = х1х2 + y1y2 = х2х1 + y2y1 = r2 • r1
Соотношения в) и г) доказываются аналогично и оставляются в качестве упражнения. //
В более общем случае, если V — векторное пространство над R и Ф: V × V → R — отображение, удовлетворяющее свойствам а) — г), то (V, Ф) становится пространством, для которого могут изучаться понятия длины и угла. Отображение Ф называют внутренним произведением для V, а (V, Ф) —векторным пространством с внутренним произведением. В частности, если определить Ф: Rn × Rn → R (n ∊ N) соотношением
Ф(а, b)
а • b
=
 ,
,
где a = (a1, ..., аn), b = (b1, ..., bn), то отображение • будет соблюдать требуемыми свойствами. Определим длину вектора a ∊ Rn как
||a|| = (а • а)1/2, а косинус угла между двумя векторами а и b как
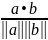
угол лежит на отрезке [0, π].
На Rn могут быть определены другие внутренние произведения. Внутреннее произведение, введенное выше, называется обычным или евклидовым внутренним произведением. Оно дает те значения длины и угла, которые ожидались интуитивно.
Когда n = 1, ясно, что • является лишь умножением в R, и угол между двумя векторами определяют арккосинусом. Угол равен или 0, пли π в зависимости от знака ху. Норма ||•|| обобщает понятие модуля |•| в R и обладает аналогичными свойствами. Например, можно показать, что
||a|| ≥ 0 для всех a ∊ Rn
||a|| = 0 тогда и только тогда, когда а = 0,
||λa|| = |λ| ||a|| для всех a ∊ Rn и λ ∊ Rn ,
||a + b|| ≤ ||a|| + ||b|| для всех a, b ∊ Rn
Вектор a ∊ Rn такой, что ||a|| = 1 (что эквивалентно а•а = 1), называется единичным вектором. Если a ∊ Rn \{0}, то a/||a|| — единичный вектор, параллельный а. Единичный вектор обычно обозначается а.
Если В
= { 1,
...,
n}—
базис в Rn
и
1,
...,
n}—
базис в Rn
и
то базис В называется ортонормированным. Ортонормированный базис в Rn, определенный следующим образом:
 i
= (0, ...,0,1,0, ...,0), l
< i
< n,
i
= (0, ...,0,1,0, ...,0), l
< i
< n,
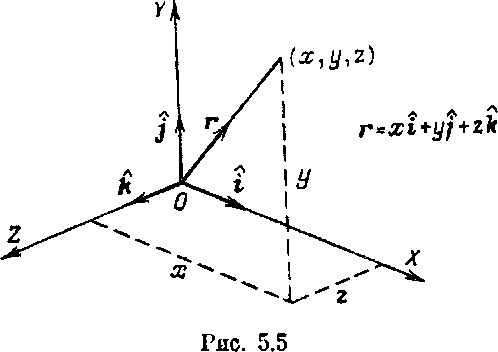
называется стандартным базисом в Rn. В R2 и R3 стандартные базисы удобно записывать в виде (i, j) и (i, j, k) соответственно. Рассмотрим следующую геометрическую интерпретацию этих базисов. Векторы i и j определяют правостороннюю систему осей в R2, а третья ось OZ перпендикулярна плоскости, содержащей векторы i j, и направлена таким образом, чтобы концы векторов 1, J и к (в указанном порядке) определяли правостороннее движение (рис. 5.5). Это свойство известно как правило правой руки. В системах такого типа в R3 оси называются правосторонними.
Определение. Если a = (а1, а2, а2) ∊ R 3 и b = (b1, b2, b2) ∊ R 3, то векторным произведением а и b (обозначается а × b) по определению называют вектор а × b = (а2b3 — а3b2, а3b1 — а1b3, а1b2 — а2b1). //
Операция × может рассматриваться как отображение R 3 × R 3 → R 3.
Предложение. Если a, b ∊ R3, то
а) ||a × b|| = ||a|| ||b|| sin θ, где θ — угол между а и b;
б) вектор а × b ортогонален векторам а и b.
Доказательство.
а) ||a × b||2 = (a2b3—a3b2) 2+(a3b1—a1b3) 2+(a1b2—a2b1) 2 =
=
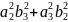 —
2a2b3a3b2
+
—
2a2b3a3b2
+
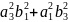 —
2a3b1a1b3
+
—
2a3b1a1b3
+
 — 2
a1b2a2b1
= (
— 2
a1b2a2b1
= (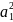 +
+
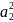 +
+
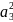 )
(
)
(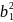 +
+
 +
+
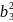 )
— (a1b1+
a2b2
+ a3b3)
2 =
)
— (a1b1+
a2b2
+ a3b3)
2 =

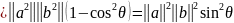
б) Легко показать, что a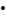 (a×b)
= 0 и b
(a×b)
= 0, откуда и следует требуемый результат.
//
(a×b)
= 0 и b
(a×b)
= 0, откуда и следует требуемый результат.
//
Чтобы получить геометрическую интерпретацию а × b, заметим, что если
a=(a1, 0,0), b=(b1, b2,0),
то
a×b = (0, 0, a1b2);
поэтому если а1 > 0, то
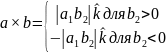
и направление а × b определено таким образом, чтобы выполнялось правило правой руки относительно векторов а, b и а × b. Это правило носит общий характер, поскольку для произвольной пары векторов в правосторонней системе координат всегда можно выбрать способ представления векторов, который определяется векторами а и b. В результате векторное произведение будет иметь вид
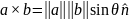
где
 — единичный вектор, ортогональный а
и b,
с направлением, выбираемым по правилу
правой руки. Если
— единичный вектор, ортогональный а
и b,
с направлением, выбираемым по правилу
правой руки. Если
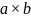 = 0, то векторы а
= 0, то векторы а
ПРЕДИСЛОВИЕ 7
ВВЕДЕНИЕ 8
ГЛАВА 1. МНОЖЕСТВА 11
§ 1. Множества н их спецификация 11
§ 2. Простейшие операции над множествами 17
§ 3. Диаграммы Венна 24
§ 4. Подмножества и доказательства 27
§ 5. Произведения множеств 36
ГЛАВА 2. ОТНОШЕНИЯ 39
§ 1. Основные понятия 40
§ 2. Графические представления 44
§ 3. Свойства отношений 48
§ 4. Разбиения и отношения эквивалентности 50
§ 5. Отношения порядка 54
§ 6. Отношения на базах данных и структурах данных 57
§ 7. Составные отношения 65
§ 8. Замыкание отношений 68
ГЛАВА 3. Функции 71
§ 1. Функции и отображения 71
§ 2. Обратные функции и отображения 75
§ 3. Мощность множеств и счетность 76
§ 4. Некоторые специальные классы функций 86
§ 5. Аналитические свойства вещественных функций 95
§ 6. Операции 110
ГЛАВА 4. ОСНОВНЫЕ ПОНЯТИЯ АРИФМЕТИКИ 120
§ 1. «Малая» конечная арифметика 120
§ 2. «Большая» конечная арифметика 125
§ 3. Двоичная арифметика 131
§ 4. Логическая арифметика 137
ГЛАВА 5. АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ 141
§ 1. Алгебраические структуры и подструктуры 142
§ 2. Простейшие операционные структуры 145
§ 3. Кольца и поля 148
§ 4. Линейная алгебра 160
§ 5. Решетка и булевы алгебры 180
§ 6. Замкнутые полукольца 202
ГЛАВА 6. МАТРИЦЫ 205
§ 1. Матрицы и бинарные отношения на конечных множествах 205
§ 2. Матрицы над другими алгебраическими структурами 212
§ 3. Матрицы и векторные пространства 216
Глава 7. Теория графов 227
§ 1. Вводные понятия 227
§ 2. Маршруты, циклы и связанность. 236
§ 3. Планарные графы 241
§ 4. Структуры данных для представления графа 248
§ 5. Обход графа 252
§ 6. Ориентированные графы 257
ГЛАВА 8. ЯЗЫКИ И ГРАММАТИКИ 273
§ 1. Основные понятия 273
§ 2. Грамматики с фразовой структурой 281
§ 3. Контекстно-свободные языки 292
§ 4. Понятия грамматического разбора и грамматических модификаций 298
§ 5. Грамматики операторного предшествования 314
ГЛАВА 9. КОНЕЧНЫЕ АВТОМАТЫ 318
§ 1. Общие понятия 319
§ 2. Конечные автоматы 337
§ 3. Регулярная алгебра 349
ГЛАВА 10.КОМПЬЮТЕРНАЯ ГЕОМЕТРИЯ 358
§ 1. Системы координат для подмножеств R3 360
§ 2. Преобразования 366
§ 3. Кривые и поверхности 387
Некоторые свойства векторного произведения приведем ниже; доказательства оставляем в качестве упражнений.
Предложение.
а)
=
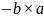 ;
;
б) 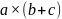 =
+
=
+
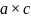 ;
;
в) 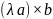 =
=
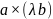 =
=
 ;
;
г)
 =
=
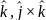 =
=
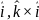 =
=
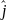 ;
;
д)  =
=
 ;
;
е)
=
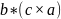 =
=
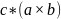 =
=
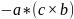 =
=
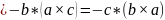 .
//
.
//
Выражение
часто называют тройным
векторным произведением
a,
b
и с,
а
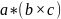 —смешанным
произведением.
Геометрически
означает объем параллелепипеда с ребрами
a,
b
и с.
—смешанным
произведением.
Геометрически
означает объем параллелепипеда с ребрами
a,
b
и с.
Предложение.
Множество {а,
b,
с}
R3
линейно зависимо тогда и только тогда,
когда
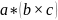 =
0.
=
0.
Доказательство. Предположим, что a, b и с линейно зависимы. Тогда существуют λ, μ, σ ∊ R, не все равные нулю, такие, что
λа + μb + σс = 0.
Не ограничивая общности, предположим, что λ 0. Тогда
а = – λ
-1 (μb
+ σс),
а
= ( )
= – λ-1
(μb
+ σс)
(
)
=
)
= – λ-1
(μb
+ σс)
(
)
=
= – λ -1 [μb ( ) + σс ( )] = 0, Обратно, если —, то или
а) один из векторов а, b, с равен нулю (в этом случае результат очевиден), или
б) вектор а
ортогонален
 .
.
Однако b и с ортогональны к ; поэтому а = λ'b + μ'с при некоторых λ', μ' ∊ R и а, b, с линейно зависимы. //
Закончим главу кратким рассмотрением вопросов дифференцируемости «векторнозначных» функций. Пусть на R" задана обычная норма. Определим производную функции вида
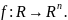
Обобщая одномерный случай, скажем, что дифференцируема в точке t, если существует вектор F(t) = (F1(t), …, Fn(t)) ∊ R n такой, что
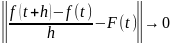
при h
→ 0, или, что эквивалентно,
если f
имеет компоненты
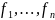 такие, что
такие, что
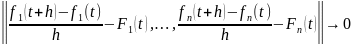
при h 0. Очевидно, что каждая компонента должна стремиться к нулю при h 0, поэтому df/dt существует тогда и только тогда, когда df1/dt ,…, dfn/dt существуют и
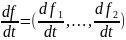
Другими словами, чтобы продифференцировать векторнозначную функцию, мы должны продифференцировать ее покомпонентно, Например, если f: R → R3 определена соотношением
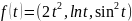
то
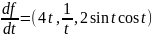
Пусть f: R → R3 и g: R → R3. Определим функции f • g: R → R и f g: R → R3. Положим
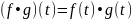 ,
,
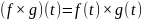
Дифференцирование этих функций производится следующим образом:
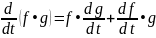 ,
,

Проверку этих формул оставляем в качестве упражнения. Упражнение 5.4.
Показать, что если V — векторное пространство над полем F, то
 для всех x
∊
V,
для всех x
∊
V,
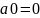 для всех a
∊
F.
для всех a
∊
F.
Представить вектор (а, 1, 3) ∊ R3, где а ∊ R, в виде линейной комбинации векторов множества
S = {(1, 1, 0), (0, 2, 0), (0, 0, 4)}
и показать, что S — линейно независимое множество векторов. Является ли S базисом в R3?
Показать, что если {x1, ..., xm} — линейно независимое подмножество векторного пространства V, то xi 0 при любом i, 1 ≤ i ≤ т.
а) Какие из следующих преобразований являются линейными:
Т1(х, у) = (а, у), а ∊ R\{0},
Т2(х, у) = (λх + у, σy), λ, σ ∊ R\{0},
Т3(х, у) = (х2, 0), T4(x, у) = (х, 0)?
б) Определить произведения Т2 ∘ Т4 и Т4 ∘ Т2.
в) Доказать, что если T ∊ End(V), то T0 = 0.
а) Если V — векторное пространство, то проекцией (проектором) V называют преобразование Р: V → V, обладающее свойством
(Р ∘ Р)х = Рх для всех x ∊ V.
Доказать, что преобразование Р: R2 → R2, определяемое соотношением
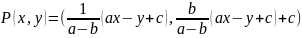
при а, b, с ∊ R и а b, является проектором в R2. При каких условиях Р ∊ End(R2)?
б) Какие из определенных в п. 4. а) преобразований являются проекторами?
Пусть Т ∊ End (V). Нулевым подпространством (ядром) T называют множество N(Т), определяемое соотношением
N(T)={x ∊ V: Тх = 0}.
Доказать, что N(Т) является векторным подпространством V. Доказать также, что образ Т является векторным подпространством V.
Пусть V — векторное пространство над R в Т ∊ End(V). Говорят, что Т имеет действительное собственное значение λ ∊ R если существует ненулевой вектор x ∊ R такой, что
Тх = λх;
при этом х называют собственным вектором Т, соответствующим собственному значению λ. а) Доказать, что если Т е End (V) такое, что
Т(х, у) = (х + ау, у),
то любой вектор вида (р, 0) при р 0 является собственным вектором Т. Какие у Т собственные значения?
б) Пусть Т ∊ End(V). Обозначим через Vλ множество собственных векторов Т, соответствующих собственному значению λ. Показать, что Vλ {0} является векторным подпространством V. Доказать аналогичное утверждение для N(Т).
Найти собственные значения и собственные векторы преобразований Т1, Т2 ∊ End (R2):
Т1(x, у) = (–у, x), Т2(х, у) = (х, –у).
Какой геометрический смысл имеют Т1 и Т2?
Доказать, что
а) если S, Т ∊ End (V), то S ∘ Т ∊ End (V);
б) если при Т ∊ End(V) существует преобразование S: V → V такое, что
S ∘ T = T ∘ S = Iv,
то S ∊ End(V);
в) если Т ∊ Aut (V), то N(T) = {0}.
Доказать, что если r1, r2, r3 ∊ R2 и λ ∊ R, то
a) r1 • (r2 + r3) = r1 • r2 + r1 • r3;
б) λ (r1 • r2) = (λr1) • r2 = r1 • (λr2);
в) |r1 – r2| ||r1|| ||r2||;
г) ||r1 – r2||2 = ||r1||2 + ||r2||2 – 2||r1|| ||r2||cos θ,
где θ — угол между r1 и r2;
д) |||r1|| – ||r2||| ≤ ||r1 + r2|| ≤ ||r1|| + ||r2||
(последнее неравенство известно как неравенство треугольника). Дать геометрические иллюстрации этим результатам.
В действительности вышесказанное имеет место для любого пространства со скалярным произведением; в частности, результаты справедливы для Rn (n ∊ N) с обычным внутренним (скалярным) произведением.
Вычислить единичные векторы, параллельные
а) а = (1, 1, 1);
б) b = (1, р, 0), p ∊ R.
Определить единичный вектор, ортогональный а и b одновременно.
Пусть а, b, с ∊ R3 и λ ∊ R. Доказать, что
а) а b = –b а;
б) а (b + с) = а b +а с;
в) (λ a) b = a (λ b) = λ (a b);
г) = = = ;
д) а (b с) = (а с) • b — (а b) • c;
е) а • (b с) = b • (с а) = с • (а b)= –а • (с b) =
= –b • (а с)= –с • (b а).
Используя результаты 5.4, 12, доказать, что операция : R3 R3 → R3 не ассоциативна, т. е. в общем случае a (b с) (а b) с.
Пусть f, g: R → R3. Доказать, что
а)
б)
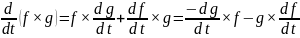
в) если ||f (t)|| = a для всех t, где а ∊ R — постоянная, то df/dt ортогонален к f при всех t. Провести вычисления при
f(t)= (с cost, a sin t, 0), g(t) = (0, 1, t).
