6.2. Маршруты и связность в орграфах.

О п р е д е л е н и е. Маршрутом длины из в в орграфе называется последовательность рёбер вида

т.е. вторая вершина каждого ребра совпадает с первой вершиной следующего ребра. //

Часто удобно представлять маршрут последовательностью вершин

которые его определяют. Если , то маршрут называют замкнутым маршрутом или циклом. Орграф без циклов называют ацикличным.

Теоремы § 2 также справедливы с аналогичными доказательствами для орграфов. Определим связность или матрицу достижимости тем же самым способом. Заметим, однако, что для орграфов отношение не является отношением эквивалентности на и, следовательно, не осуществляет разбиения

Пусть обозначает множество всех орграфов, а – множество всех графов. Мы можем определить отображение следующим образом.

О п р е д е л е н и е. Пусть . Тогда множество вершин совпадает с , а множество рёбер определяется применением следующих операций на :

а) удаляются все петли из ;

б) заменяются на [ для всех .

Тогда является графом, связанным с орграфом . //

Для орграфов понятие связности является более содержательным, чем для графов, и имеет отношение к проблеме обхода. Сейчас мы определим три важных типа связности орграфа.

О п р е д е л е н и е. Если – орграф , то будем говорить, что:

а) слабо связный, если граф связный;

б) односторонне связный, если для каждой пары различных вершин существует маршрут из в или обратно,

в) сильно связный, если для каждой пары различных вершин существует маршрут из в и обратно. //

Очевидно, что сильно связный односторонне связный слабо связный.

П р и м е р 6.2. Из рис 7.22 мы видим, что орграф:

а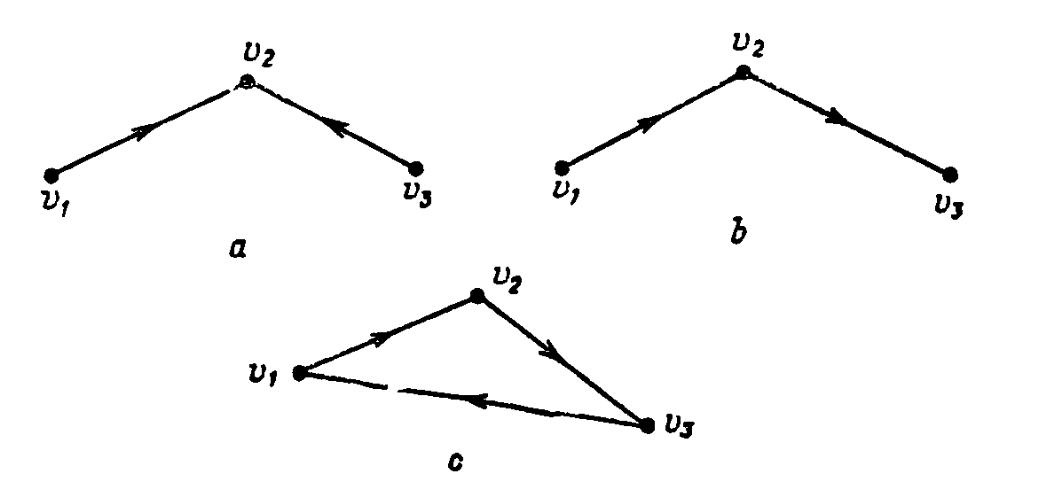 ) только слабо связный (рис. 7.22, а);

б) односторонне связный, но не сильно связный (рис. 7.22, b);

в) сильно связный (рис. 7.22, c).

Рис. 7.22

В терминах связности матрицы орграф сильно связный тогда и только тогда, когда всех , ; односторонне связный тогда и только тогда, когда всех , .

П р и м е р 6.3. Рассмотрим орграф, представленный диаграммой на рис. 7.23. Для этого орграфа

, ,

, ;

поэтому для

имеем всех , и, следовательно, граф является сильно связным. Для более эффективного вычисления можно использовать алгоритм Уоршолла. //

Если – орграф, то можно разбить путём определения отношения эквивалентности следующим образом:

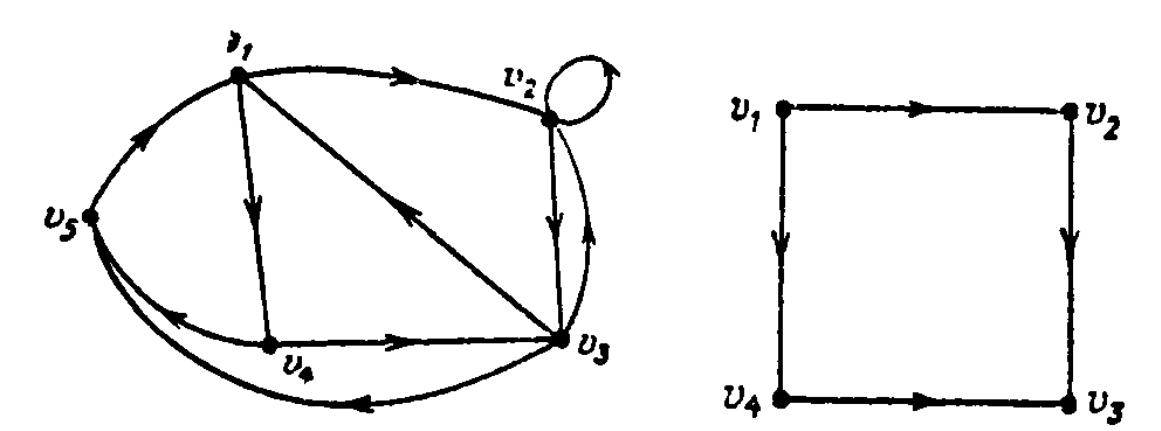
Рис. 7.23 Рис. 7.24

, если или существуют маршруты из в и обратно. Если – разбиение и , а являются соответствующими множествами рёбер, то подграфы ( ) называются сильно связными компонентами .

Очевидно, что и может быть определено из как ; граф сильно связный тогда и только тогда, когда имеет только одну сильно связную компоненту, т.е. если .

П р и м е р 6.4. Для орграфа на рис. 7.24 имеем

; .

Таким образом, ( ) являются сильно связными компонентами графа. //

Пусть G = (V, Е) — ациклический орграф. Вершину называют листом, если δ⁺( ) = 0. Если ( , ) ∈ E, то является непосредственным предком , а — не­посредственным потомком . Если существует маршрут из в , то говорят, что является предком , a — потомком .

Эти понятия не имеют смысла для орграфов, имею­щих циклы, так как для таких графов вершина может исходить сама из себя.

Пример 6.5. Для ациклического орграфа, изобра­женного на рис, 7.25, из вершин , и ребра не выходят, является предком , является прямым потомком и т. д.

Существует тесная связь между ациклическими ор­графами и частично упорядоченными отношениями. В ча­стности, имеет место следующий результат, доказатель­ство которого мы оставляем в качестве упражнения. За­метим, что для сокращения некоторых

Р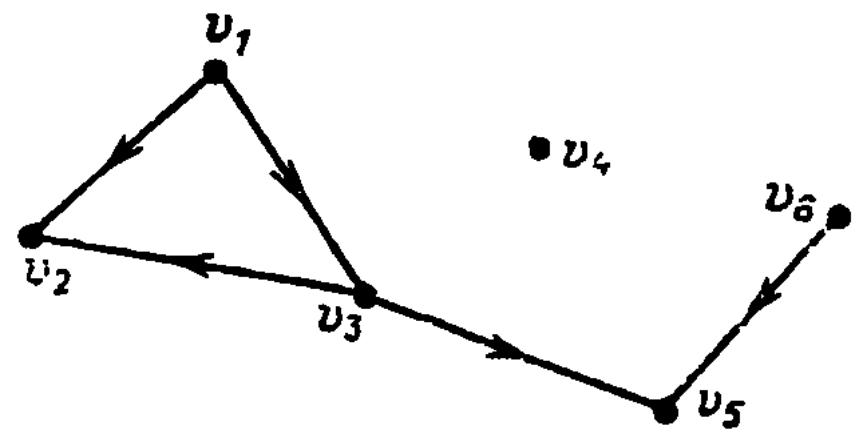 ис. 7.25

доказательств, приведенных ниже, частичные порядки будут основаны скорее на отношении <, чем на отношении ≤, и, следовательно, являются транзитивными и нерефлексивными.

Предложение.

а) Пусть отношение < является частичным отношением порядка на конечном множестве V. Тогда, если

E={( , ): < },

то пара G = (V, Е) является ациклическим графом.

б) Пусть G — (V, Е) —ациклический орграф и отношение < определяется следующим образом; < , если является предком . Тогда отношение < является частичным отношением порядка на V. //

В терминах орграфов можно дать точное определение структурам данных, известным как ориентированное де­рево.

Ориентированное дерево T = (V, E) — это ациклический орграф, в котором одна вершина V не имеет предков, а каждая другая вершина имеет только одного непосред­ственного предка; называется корнем дерева. Бинар­ное дерево — это ориентированное дерево, в котором каж­дая вершина имеет не более двух непосредственных по­томков, т. е. δ⁺( ) ≤ 2 для всех V. Говорят, что би­нарное дерево является полным, если каждая вершина, не являющаяся листом, имеет ровно два непосредственных потомка.

П р е д л о ж е н и е. Следующие утверждения эквива­лентны по отношению к орграфу G = (V, Е):

а) G является деревом.

б) Граф F(G) связный, и существует вершина , которая не имеет предков, а все другие вершины имеют только по одному непосредственному предку.

в) G имеет вершину , которая соединяется с любой другой вершиной единственным маршрутом.

г) G имеет вершину , которая не имеет предков; все другие вершины имеют только одного непосредственного предка; существует маршрут к каждой вершине из .

Доказательство оставляем в качестве упражнения. //

6.3. Упорядоченные орграфы и обходы. Списки смеж­ности являются альтернативной по отношению к матрице смежности формой представления орграфов. Заданное списком смежности представление определяет порядок ребер, выходящих из каждой вершины.

Определение. Упорядоченным орграфом называ­ется пара G = (V, Е), где V — конечное множество вер­шин, а Е — множество упорядоченных списков ориенти­рованных ребер. Элементы E имеют вид

= (( , ), …, ( , )),

где , . //

Пример 6.6. Упорядоченный орграф

может быть представлен списками смежности

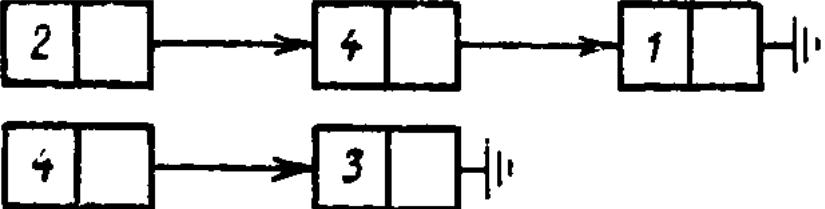
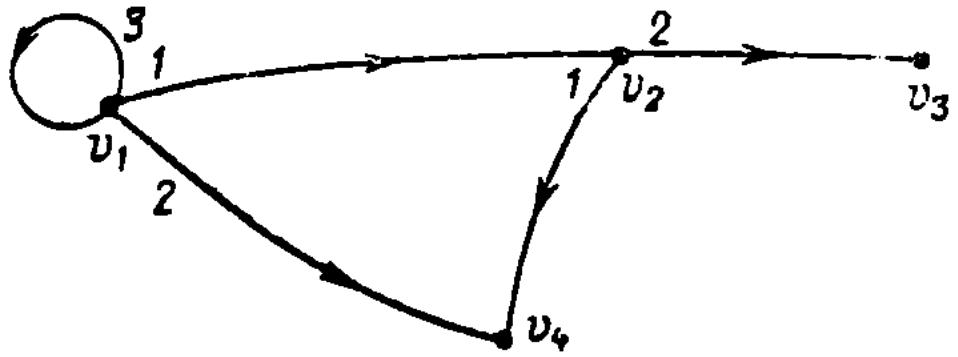
и может быть изображен диаграммой (рис. 7.26).

Рис. 7.26

Упорядоченный орграф G определяет единственный неупорядоченный орграф; мы только заменяем каждый список (( , ), …, ( , )) множеством {( , ), …, ( , )}. Орграф, определенный таким образом, на­зывают орграфом, подчиненным G. Упорядоченный ациклический орграф является упорядоченным графом, чьим подчиненным орграфом является ациклический ор­граф. Упорядоченное ориентированное дерево является упорядоченным орграфом, чей подчиненный орграф яв­ляется ориентированным деревом.

Пример 6.7.

я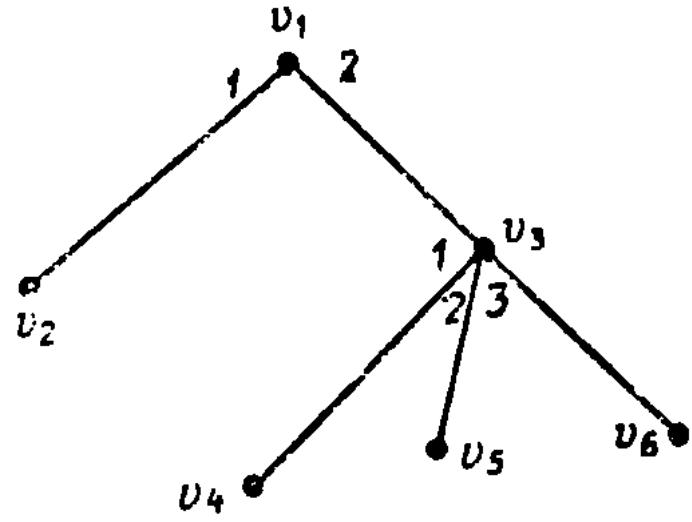 вляется упорядоченным ориентированным деревом — корень. Оно может быть изображено, как показано па рис. 7.27. //

Упорядоченные ориентированные деревья будем изображать спуском вершин слева направо (рис. 7.27). Если принять такое соглашение, то номера ребер можно опускать.

Определение. Рис. 7.27

1. Пусть S_V и S_B — множества. Пометкой упорядоченного орграфа G = (V, Е) называется пара отображе­ний (f, g), где

f: V → S_V — пометка вершин,

Отображение g имеет вид

2. Говорят, что два помеченных графа G₁ = (V₁, Е₁) и G₂ = (F₂, Е₂) с функциями пометок (f₁, g₁) и (f₂, g₂) соответственно эквивалентны, если существует биекция h: V₁ → V₂ такая, что

a) (( , ), …, ( , )) ∈ E₁ тогда и только тогда, когда

((h( ), h( )), …, (h( ), h( ))) ∈ E₂

(эквивалентны как упорядоченные графы);

б) f₁( ) = f₂(h( )) для всех (метки вершин совпадают);

в) для всех (( , ), ( , ), …, ( , )) ∈ E₁ имеем

g₁((( , ), .... ( , ))) = g₂(((h( ), h( )), ..., (h( ), h( ))))

(метки ребер совпадают). //

Следуя § 5, определим обход орграфа как перестанов­ку или полное упорядочивание вершин. Для упорядочен­ных орграфов все делается точно так же. Для упорядо­ченных ориентированных деревьев часто полезны другие обходы. Некоторые из них будут описаны ниже.

О п р е д е л е н и е. Пусть T = ({ , …, }, Е) — упо­рядоченное ориентированное дерево и = (( , ), …, ( , )) ∈ E. Определим отношение < на множестве { , …, } следующим образом: < тогда и только тогда, когда i < j. Определим таким образом отношение < для каждого списка Е. //

П р е д л о ж е н и е. Отношение < является отношени­ем частичного порядка на V.

Д о к а з а т е л ь с т в о.

Из соотношения < следует список вида

который невозможен, так как в дереве не существует циклов. Следовательно, ≮ для любого .

Из соотношений < и < следует, что сущест­вуют х, у ∈ V такие, что

Если х ≠ у, то = 2, что невозможно, так как T — дерево. Следовательно, х = у и

т.е. < u. Поэтому отношение < есть частично упорядо­ченное отношение на V. //

Отношение < сравнивает только вершины, выходя­щие из одной вершины.

П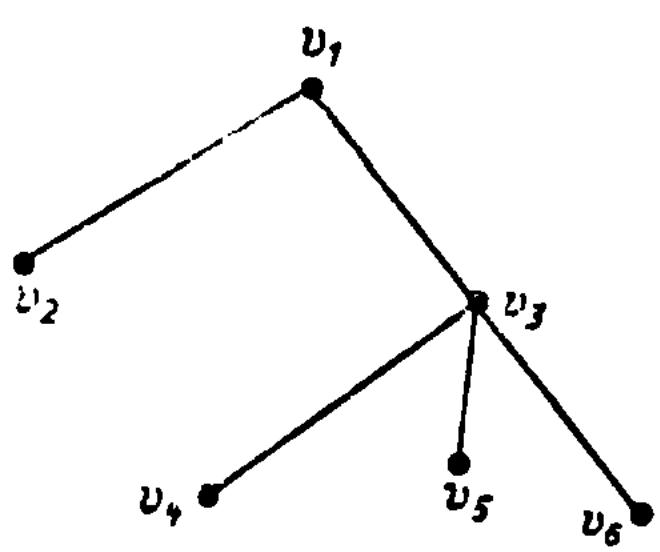 р и м е р 6.8. Для упорядоченного ориентированного дерева на рис. 7.28 имеем

<={( ), ( ), ( ), ( )} или

//

Замечание. Обозначим множество всех спусков из вершины через Г⁺( ); аналогично через ( ) обозначим множество входов в .

Рис. 7.28

О п р е д е л е н и е. Отноше­ние < называют трансверсальным порядком вершин упоря­доченного направленного дере­ва T = (V, E). //

Наша цель в оставшейся части главы — вывести различные полезные методы обхода для дерева с использованием симметрии путей расширения трансверсального порядка. Перед точным определением об­ходов необходимы два результата. Пусть < определяет отношение <, на V следующим образом: если , то для всех и для всех

Предложение.

1. < ⊆ <_e;

2. < _e — частично упорядоченное отношение на V. Доказательство.

1. Утверждение очевидно.

2. а) Из <_e следует, что или < , или существу­ют х, y ∈ V такие, что х < у и и . Однако , так как < — отношение час­тичного порядка. Аналогично из х < у следует х ≠ у; сле­довательно, и . Однако это означает, что или для некоторого . Это невозможно, потому что T = (V, E) —де­рево. Таким образом, <_e для всех

б) <_e означает, что v < w или что существуют х, y ∈ V такие, что х < у и и ; <_eu означает, что w < u или что существуют r, s ∈ V такие, что r < s и и ; и дают, что или , пли .

Следовательно, дерево имеет одну из форм, изобра­женных на рис. 7.29. Если , то и x < y дает x <_e s. Однако , следовательно, x<_eu, и так как , то, следовательно, <_e . Если , то и r < s дает x <_e s. Однако , следовательно, х<_eи, a дает <_e .

Следовательно, <, является отношением частичного порядка на V. //

Иногда <_ew читают как « находится слева от w».

Р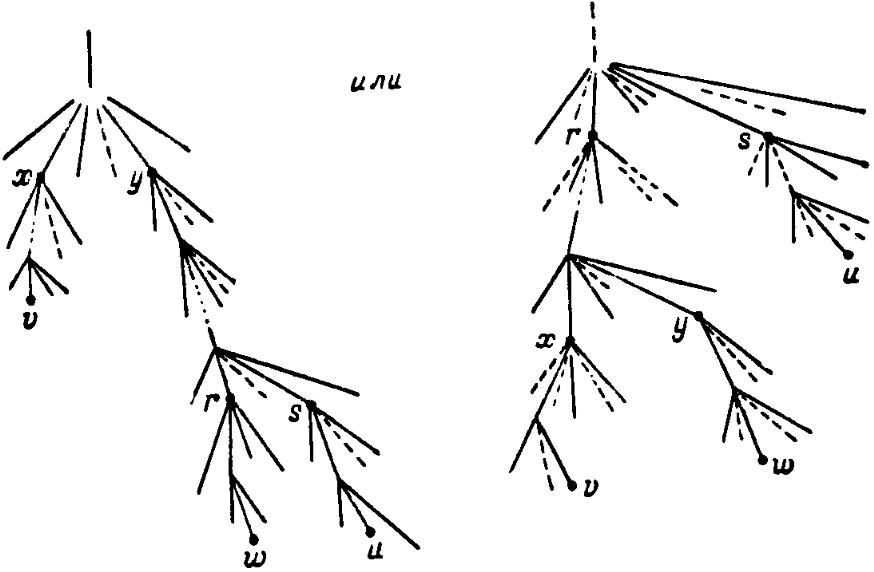 ис. 7.29

Предложение. Пусть T = (V, Е) — упорядоченное ориентированное дерево. Тогда для или <_e , или <_e , или же и находятся на маршруте.

Доказательство. Пусть и . Тогда существует вершина , такая, что и . Если = или = , то и нахо­дятся на маршруте; в противном случае рассмотрим пря­мые спуски из . Тогда или

и для

или

В первом случае имеем или <_e или <_e в за­висимости от того, или . Во втором слу­чае повторяем процесс из пока не будут выполнены условия первого случая, или получаем = или = в этом случае и находятся на маршруте. //

Много полезных обходов дерева определяют посред­ством расширения отношения <_e до полного упорядочи­вания V. Используя приведенный выше результат, надо только расширить <_e, чтобы сравнивать вершины, кото­рые находятся на маршруте, для определения полного порядка на V, для которого <_e является подпорядком.

Определение. Пусть T = (V, Е) — упорядоченное направленное дерево. Определим полную упорядоченность <₁ на V следующим образом: если спускается из , то <₁ в противном случае <₁ , если <_e . От­ношение <₁ называют предпорядком на V. //

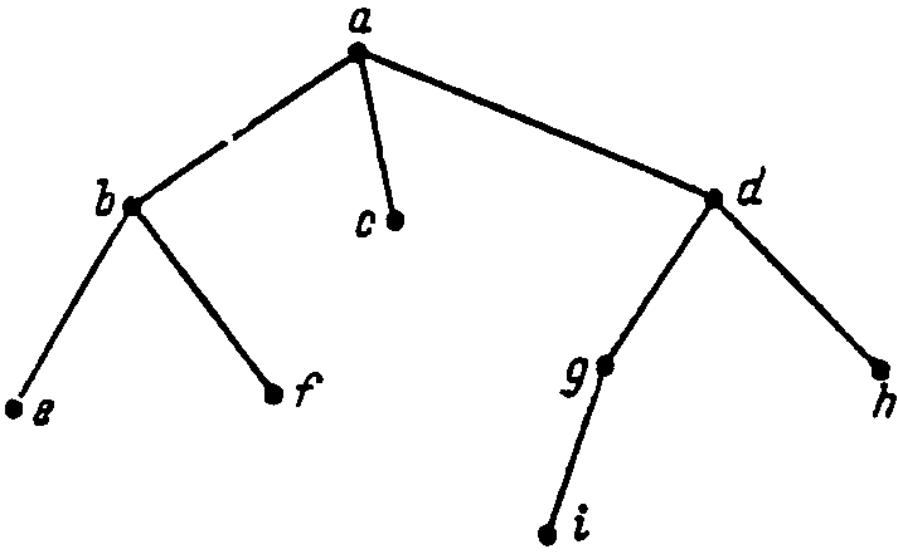О чевидно, что <_s ⊆ <_I.

Рис. 7.30

Пример 6.9. Пусть T = (V, Е) - упорядоченное на­правленное дерево, изображенное на рис. 7.30. Тогда предпорядок на V = {а, b, c, d, e, f, g, h, i} можно запи­сать как

a <₁b <₁e <₁f <₁ c <₁d <₁g <₁i <₁h.

Соответствующий обход вершины имеет вид а, о, a, b, e, f, c, d, g, i, h. //

Определение. Пусть T = (V, Е) — упорядоченное ориентированное дерево. Определим отношение <₂ пол­ного порядка на V следующим образом: если спускает­ся из , то <₂ ; в противном случае <₂ , если <_e . Отношение <₂ называют постпорядком на V. //

Очевидно, что <_e ⊆ <₂.

Пример 6.10. Пусть T и V такие же, как и в пре­дыдущем примере. Тогда постпорядок на V будет иметь вид

e <₂ f <₂b <₂c <₂ i <₂g <₂h <₂d <₂a

с обходом

e, f, b, c, i, g, h, d, a. //

Определение. Пусть T = (V, Е) — полное бинар­ное дерево. Определим симметричный порядок <₂ на V следующим образом: для каждой вершины, не являющей­ся листом и имеющей прямые спуски и ( < ), положим

<_s для всех ,

<_s для всех . //

Порядок <_s также является расширением <_e.

П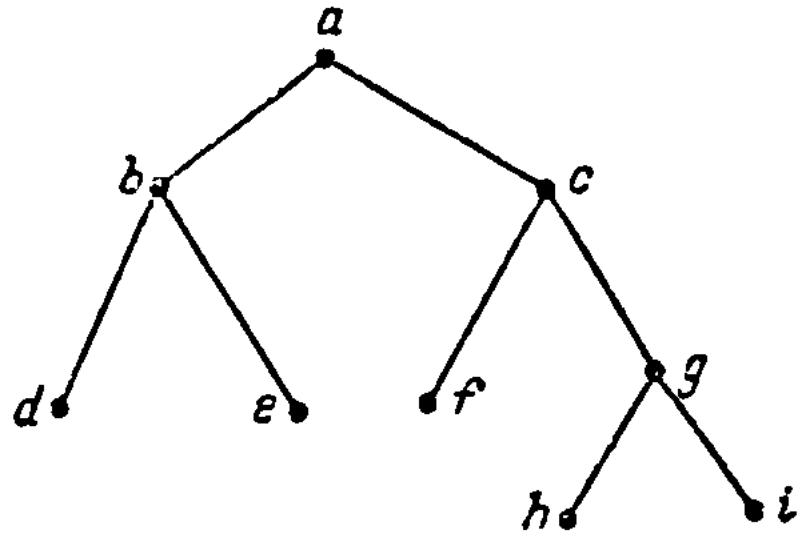 ример 6.11. Пусть T — дерево, изображенное на рис. 7.31. Тогда <_s определено, как показано на рис 7.31.

Рис. 7.31

Обход по предпорядку упорядоченного ориентирован­ного дерева соответствует обходу по глубине с корнем в качестве начальной вершины.

Если T = (V, Е) — упорядоченное ориентированное де­рево, то вершины T могут быть расположены в предпорядок с применением следующего алгоритма, начинаю­щегося с корня:

procedure pre( )

process

if do pre( ) for each

endproc

Соответствующий алгоритм для постпорядка имеет вид

procedure post( )

if then process

else begin

post( ) for each

process

end

Упражнение 7.6.

1. Пусть – матрица смежности орграфа. Выписать выражения для функций и в терминах A.

2. Сколько различных орграфов может существовать на вершинах?

3. Пусть – орграф. Какое максимально возможное значение величины ?

4. Пусть – орграф, где и . Определить матрицы и .

5. Дать матричные характеристики слабой, односторонней и сильной связности в орграфе.

6. Пусть – ацикличный орграф. Какое максимально возможное значение величины ?

7. Доказать два последних в п. 6.2.

8. Показать, что если – полное бинарное дерево и обозначает множество уходов из T, то .

9. Поддеревом ориентированного дерева называется такое ориентированное дерево, что:

1. ;

2. ;

3. ни одна из вершин V\V’ не является спуском вершины в V’. Нарисовать все поддеревья

.

10. Определение. Если T – ориентированное дерево, то уровень вершины определяют до листа. Глубина вершины – это длина пути от корня до этой вершины. Глубиной T называют длину самого длинного маршрута в T. Высотой вершины T называют глубину T за вычетом глубины вершины. Высота T является высотой корня. //

Пусть T – ориентированное дерево.

,

1. нарисовать T со значениями уровней в качестве меток вершины;

2. нарисовать T со значениями глубин в качестве меток вершины;

3. нарисовать T со значениями высот в качестве меток вершин;

4. чему равна глубина T?

5. Чему равна высота T?

11. Пусть T – ориентированное дерево. Разрезом C дерева T называется подмножество вершин T таких, что

1. не существует двух вершин C на маршруте в T;

2. ни одна вершина не может быть добавлена к C без нарушения а).

Рис. 7.32

О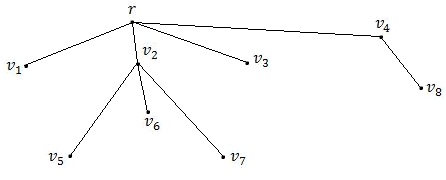 пределить все разрезы ориентированного дерева, изображенного на рис. 7.32.

12. Пусть - полное бинарное дерево и . Показать, что существует полных порядков на V, которые расширяют трансверсальный порядок <.

13. Проинтерпретировать и <_s для бинарных деревьев, связанных со структурой арифметических выражений, как в § 6 гл. 3.