5.4. Остовные леса обходов по глубине и ширине.

Пусть – граф, а – обход . тогда определяет подмножество из следующим образом: тогда и только тогда, когда используется при построении обхода. Так как для упорядоченных графов обход определяет аналогичным путём подсписок каждого списка удалением всех пар , которые не использованы в сечении.

П р е д л о ж е н и е. Пусть –упорядоченный связный граф, а – обход по глубине или ширине графа . Тогда

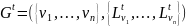
есть упорядоченное остовное дерево для .

Д о к а з а т е л ь с т в о. Так как – связный граф, то подграф 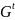также связен и является остовным для . Если содержит замкнутый маршрут, тогда некоторые вершины появляются более одного раза в , но так как – обход, то это невозможно, и является ацикличным графом. Следовательно, – дерево. //

С л е д с т в и е. Каждый связный граф имеет остовное дерево. //

Рис. 7.19

П р и м е р 5.3. Для графа из примера 5.1 остовными деревьями, определёнными первичными обходами по глубине и ширине с начальной вершиной , будут деревья, изображённые соответственно на рис. 7.19, а и 7.19, b.

Для графов, не являющихся связными, полные обходы по глубине или ширине определяют остовный лес.

У п р а ж н е н и е 7.5.

1. Пусть – упорядоченный граф, определяемый следующими списками:

.

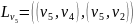Определить:

а) обход по глубине с начальной вершиной ;

б) обход по ширине с начальной вершиной

2. Нарисовать остовные деревья, соответствующие обходам упражнения 7.5.1.

3. Пусть матрица смежности графа имеет блочную структуру

г де каждое является квадратной матрицей с булевыми элементами, а все остальные элементы равны нулю. Что можно сказать о свойствах ?

4. Написать процедуры на каком-нибудь языке программирования для определения обходов по глубине и ширине.

§ 6. Ориентированные графы

6.1. Введение. Во многих приложениях теории графов требуется, чтобы рёбра графа имели направление. Например, поток данных проходит через программу.

О п р е д е л е н и е. Ориентированный граф (орграф) есть пара вершин , где – конечное множество вершин, а - произвольное подмножество . //

П р е д л о ж е н и е.

а) Ориентированный граф определяет отношение на .

б) Пусть – конечное множество. Тогда отношение на определяет ориентированный граф, у которого множество вершин –

Д о к а з а т е л ь с т в о.

а) Как и в § 1, определим следующим образом: тогда и только тогда, когда . Очевидно, что – отношение.

б) Если – отношение на , то ориентированный граф , определяемый на , имеет множество рёбер , где , тогда и только тогда, когда . //

Направление ребра обозначают порядком в ; например, если , то говорят, что ребро выходит из и входит в . На диаграмме в этом случае для указания направления используют стрелки.

П р и м е р 6.1.

Пусть , а . Тогда матрица смежности и изображение орграфа будут такими, как на рис. 7.20.

Р ис. 7.20

Аналогично на рис. 7.21 приведена матрица смежности и изображение графа , где

. //

П оскольку рёберное отношение для орграфа не обязательно симметрично или нерефлексивно, то, вообще говоря не обязательно, чтобы или .

Рис. 7.21

Рёбра типа называют петлёй. Степень вершины может быть записана в виде суммы , где – число рёбер входящих в , а – число рёбер, выходящих из . Множества и называют соответственно входящим узлом и выходящим узлом вершины . Понятия эквивалентности и пометки обобщаются на орграфы естественным образом.