§ 3. Матрицы и векторные пространства

Результаты § 2 показывают, как можно применять матрицы для проверки выполнения отношений между ко­нечными множествами соответствующих размеров. Цель этого параграфа — показать, как использовать матрицы над нолем (R, , +) (далее просто, R) для того, чтобы выполнять некоторые преобразования, в частности линей­ные преобразования в векторном пространство V над R. В замечании из § 4 гл. 5 было установлено, что если Т End(V) — множество линейных преобразовании V, то

{(х, Тх): х Т} V V

является бинарным отношением над V. Мы ищем резуль­тат применения линейного преобразования на V в (п, R), где п = dim (V).

Возможны два обобщения. Первое — рассмотрение произвольных полей, второе — линейные преобразования между векторными пространствами произвольных размер­ностей, которые могут быть определены аналогичным об­разом в (n, m, R). Так как эти обобщения нам не по­требуются, то в дальнейшем рассматривать их не будем.

3.1. Матричные представления линейных преобразова­ний. Операции сложения и умножения матриц в (п, R) неявно были определены в § 2. Если А (п, R) имеет элементы А_ij и R, определим А (п, R) как мат­рицу с элементами А_ij. Эту операцию называют умноже­нием матрицы на скаляр. Поскольку (п, R) играет центральную роль в оставшейся части этой главы, то по­лезно перечислить все его свойства относительно опреде­ленных выше операций. Единичную матрицу в (п, R) будем обозначать через I при всех п N.

Предложение. (п, R) является линейной алгеб­рой. //

Мы не даем доказательства этого факта. Рекомендуем вначале проверить выполнение аксиом линейной алгебры для (2, R), после чего будет видно, как можно постро­ить доказательство в общем случае. Надо показать, что:

а) (п, R) является векторным пространством;

б) (п, R) — кольцо;

в) умножение матрицы на скаляр обладает следующим свойством:

(АВ) = ( А)В = А( В) для всех R, А, В (п, R).

Полезно иметь специальное обозначение для подмно­жества обратимых матриц из (п, R). Обозначим это подмножество через

GL(n, R) ={А (п, R): А^-1 существует}.

Каждое GL(n, R), п N, определяет группу по умноже­нию. Эти группы называют полными линейными груп­пами.

Пусть V — векторное пространство размерности п над R и T End(V). Если B={e₁,…,e_n} — базис в V, то очевидно, что Te_i V для всех i, 1 ≤ i ≤ п. Следователь­но, должны существовать t_ij R (1 ≤ i, j ≤ n) такие, что

Te₁ = t₁₁e₁ + t₂₁e₂+…+t_n1e_n,

. . . . . . . . . . . .

Te_n = t_1ne₁ + t_2ne₂+…+t_nne_n.

Пусть A_T – матрица вида

тогда ее называют матрицей преобразования Т в базисе В. Для данного В матрица А_T единственна; таким об­разом, мы можем определить отображение

следующим образом:

Так как А_T можно вычислить, то ее можно использовать для нахождения Т.

Предложение. Пусть T End(V) соответствует матрица А_T в базисе B ={e₁,…,e_n}. Тогда, если x V-вектор

то

где

Следовательно, в данном базисе линейное преобразование Т можно выполнить с помощью произведения A_T , где А_T имеет размерность п п, а — вектор (матрица размер­ности п 1)

соответствующий х V. На самом деле можно устано­вить гораздо больше. Ниже мы установим важные свойст­ва .

Предложение. Отображение : End(V) (п, R) является изоморфизмом линейной алгебры с обычными операциями в End(V) и (n, R) на R, при­чем сужение на группу Aut(V) End(V) является группой изоморфизмов на GL(n, R).

Доказательство. Отметим основные моменты. Чтобы избежать большого количества индексов, ограни­чимся случаем п = 2. В общем случае доказательство ана­логично. Изоморфизм линейной алгебры следует из сле­дующих утверждений:

а) биективно;

б) (I_v) =I;

в) (ST) = (S) (T) для всех S, T End(V);

г) ( S + T) = (S) + (T) для всех S, T End(V) и , .

Докажем некоторые из этих утверждений; остальные оставим в качестве упражнений. Пусть {e₁, e₂} — ба­зис в V.

а) Чтобы доказать, что инъективно, необходимо показать, что

(S) = (T) S = T.

Если

Se₁ = s₁₁e₁ + s₂₁e₂, Те₁ = t₁₁e₁ + t₂₁e₂,

то

(S) = (T) s₁₁ = t₁₁, s₂₁ = t₂₁.

Поэтому Se₁ = Te₁. Аналогично Se₂ = Те₂. Следовательно, S и Т совпадают на базисных элементах c₁ и е₂. Однако для всех х V выполняется соотношение

х = e₁ + е₂;

таким образом,

Sx = Se₁+ Sе₂ = Te₁ + Tе₂=T( e₁+ е₂) = Tx, т.е. S = T.

Доказательство сюръективности оставляем в качестве упражнения.

б) I_vx = х для всех х V; следовательно,

I_ve₁=e₁+0e₂, I_ve₂=0e₁+e₂,

в) Пусть

тогда

Te₁=t₁₁e₁+t₂₁e₂,

STe₁ = t₁₁Se₁+t₂₁Se₂ = t₁₁(s₁₁e₁+s₂₁e₂) + t₂₁(s₁₂e₁+s₂₂e₂) =

= (t₁₁s₁₁+ t₂₁s₁₂)e₁ + (t₁₂s₂₁+ t₂₁s₂₂)e₂.

Аналогично

STe₂= (t₁₂s₁₁+ t₂₂s₁₂)e₁ + (t₁₂s₂₁+ t₂₂s₂₂)e₂.

Следовательно,

что и требовалось доказать.

г) Утверждение доказывается аналогично утверждению в).

Чтобы показать, что сужение на Aut(V) является группой изоморфизмов, используем свойства б)—г). Пусть Т Aut(V); тогда

Следовательно,

Т Aut(V) GL(n, R),

//

Этот результат играет существенную роль, так как имеет много важных следствий. Выведем некоторые из них. В фиксированном базисе отображение Т А_T из End(V) в (п, R) биективно (каждому преобразованию соответствует едипствеппая матрица и наоборот). Далее

(S, T)

(A_S, A_T) A_S A_T

это эквивалентно тому, что диаграмма па рис. 6.3 коммутативна. На практике это просто означает, что матрица произведения преобразований S T в End(V) может быть вычислена путем умножения матрицы A_S на матрицу A_T. Нет необходи­мости явно определять S T, а затем вычислять на основе определе­ния. Аналогичные резуль­таты получаются и для S + T. Кроме того, для сужения на обратимые преобразования Aut(V) получаем

это означает, что для вычисления необходимо лишь найти матрицу, обратную к

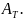
Подчеркнем еще раз, что изоморфизм зависит от базиса; в другом базисе мы будем иметь другой изомор­физм между End(V) и (п, R). Таким образом, элемент (п, R) может рассматриваться как представление эле­мента End(V) в фиксированном базисе или как представ­ление различных элементов End(V) в различных бази­сах. В гл. 10, где результаты этого параграфа будут при­меняться к Rⁿ (n = 2, 3, 4), отображение будет рас­сматриваться в стандартном базисе {e₁, …, е_n}, как это определялось в § 4 гл. 5. Для этого базиса, если х = (x₁, …, x_n) Rⁿ, то

Пусть отображение T End(V) имеет собственный век­тор х V, соответствующий собственному значению R. Тогда, если в базисе B = {e₁, …, e_n}простран­ства V вектор х имеет вид

то

Поэтому координатные вектора в представлении х явля­ются собственными векторами , соответствующими то­му же самому собственному значению.

3.2. Некоторые другие понятия теории матриц. Опре­делим теперь на (п, R) отображение, называемое де­терминантом (определителем):

det: (п, R) R.

Было бы естественным ввести это понятие и исследовать его свойства в § 4 гл. 5, так как det не зависит от базиса. Это означает, что еслп (п, R) и (п, R) — матрицы отображения T End(V) в базисах B и B' со­ответственно, то det = det . Однако, чтобы опре­делить det на End(V), мы должны были бы ввести поня­тия из тензорной алгебры. Вместо этого дадим хорошо известное определение det на (п, R) и установим не­которые из наиболее важных его свойств.

Определение det будем давать при помощи рекурсии. Вначале определим det для случая (2, R). Пусть

Тогда

detA = a₁₁a₂₂ – a₂₁a₁₂.

Если (п, R) имеет элементы а_ij (1 ≤ i, j ≤ n), то минором элемента а_kl называется матрица (п-1, R), полученная из A путем вычеркивания k-й строки н l-го столбца. Теперь det: (п, R) R мож­но определить рекурсивно для всех п N как

Иногда эту формулу называют разложением по первой строке. Можно показать, что если использовать любую другую строку или столбец для формирования соответ­ствующего выражения, то сумма будет равна detA. Другими словами,

Для малых значений n каждая из этих формул подходит для непосредственного вычисления detA. Чтобы миними­зировать число операций разложения, следует начинать со строки или столбца, содержащих наибольшее количе­ство нулей. Подчеркнем, однако, что эти разложения яв­ляются в общем случае не подходящими для вычисле­ния и существуют более эффективные вычислительные процедуры для нахождения det. Некоторые важные свой­ства det приведены ниже.

Предложение. Отображение det: (п, R) R удовлетворяет следующим условиям:

а) det I=1;

б) det А = det A^T для всех A (п, R);

в) det A = ⁿ det A, R, A (п, R);

г) det AB = detA detB;

д) A GL(n, R) тогда и только тогда, когда det А ≠ 0 . //

Мы не будем давать доказательства этих утверждений.

Предлагаем читателю проверить их для (2, R). Заме­тим также, что свойство д) характеризует GL(n, R).

Удобно выделить некоторые матрицы с «особыми» свойствами, которые будут использоваться в дальнейшем. Если A (п, R) и А = А^T, то говорят, что А симмет­рична; если А = -А^T, то матрица А кососимметрична. Если

АА^Т = А^ТА=I (т. е. А^-1=А^T),

тогда говорят, что А ортогональна. Множество всех ор­тогональных матриц (п, R) обозначается через 0(п). Через SO(п) обозначим подмножество 0(п), состоя­щее из матриц с единичным детерминантом. Элементы SO(n) называют специальными ортогональными матри­цами.

П р е д л о ж е п и е.

а) О(п) является подгруппой GL(n, R);

б) SO(n) является подгруппой 0(п). Доказательство.

в) Надо показать, что О(п) замкнуто по умножению и для каждой А О(п) существует обратная матрица A^-1 О(п). Если А, B О(п), то АА^Т = А^ТА =I и ВВ^Т = В^ТВ = I; следовательно,

(АВ) (АВ)^T – АВ(В^ТА^Т) = А(ВВ^Т)А^Т = АА^Т = I.

Аналогично (АВ)^ТАВ = I, и, следовательно, АВ О(п). Если А О(п), то

(А^-1) (А^-1)^T = А^Т(А^Т)^Т = А^ТА = I.

Следовательно, А^-1 О(п).

б) Доказательство в этом случае осуществляется по­добным образом и оставляется в качестве упражнения. //

Завершим этот параграф кратким обсуждением функ­ций от матриц. Подобно det, это следовало бы рас­сматривать в § 4 гл. 5. Однако у нас нет аппарата для рассмотрения сумм с бесконечным числом слагаемых в End (V). Результаты в (п, R), приведенные ниже, до­статочны для наших целей.

Пусть А (п, R), тогда матрица А² (п, R) — это по определению матрица АА. Аналогично можно опреде­лить А^k для всех k N, k > 2; положим А⁰ = I. Следова­тельно, если

р: R R

есть полиномиальная функция

то определим р(А) (п, R) как

Такая матрица существует, поскольку (п, R) — век­торное пространство. Эту идею можно обобщить. Если f: R R разлагается в сходящийся ряд

может быть идентифицировано с . На можно определить норму, как указано в § 4 гл. 5. Тогда это ин­дуцирует норму на (п, R), и в этом случае бесконеч­ные суммы имеют смысл. В частности, если A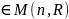 , то можно показать, что

всегда существует в и записывается как ехрA или же е^A. Когда n = 1, ехр является обычной экспонен­циальной функцией, однако при п > 1 функция ехр ведет себя совершенно иным образом (см. упражнение 6.3).

Упражнение 6.3.

1. Доказать, что с обычными операциями яв­ляется линейной алгеброй.

1. 1) Определить матрицы линейных преобразований

Т₁(х, у) = (2х+2у, -х-у),

( )

Т₂(х, у) = (2х + у, -х)

пространства R² в

а) стандартном базисе R²;

б) базисе B' = {(1, 0), (1, 1)}.

2. Вычислить координаты вектора а = (-1, 7) в бази­се B' и определить вектор Т₁Т₂a, используя матричное представление.

С помощью понятия детерминанта определить, ка­кие из преобразований ( ) обратимы. Является ли про­изведение Т₁Т₂ обратимым?

3. Пусть

Определить, является ли каждая из этих матриц сим­метричной, кососимметричной, ортогональной, обратимой.

4. Показать, что у кососимметричной матрицы элемен­ты, стоящие на диагонали, равны нулю.

5. 1) Доказать, что собственные значения симметрич­ной (2 2)-матрицы всегда действительны.

2) Доказать, что собственные числа ненулевой косо-симметричной (2 2)-матрицы не являются действи­тельными.

6. Пусть А . Доказать, что

(Аа) • b = а • (А^Тb) для всех а, b Rⁿ,

и использовать этот факт для доказательства того, что ес­ли A симметрична, то собственные вектора, соответствую­щие различным собственным значениям, ортогональны,

7. 1) Пусть

(

и p(x)=x²-4x+5. Доказать, что p(A)=0.

2) Использовать ( для вычисления обратной матрицы A^-1.

8. 1) Пусть

Используя индукцию, доказать, что

для всех n N, т. е. показать, что е^А = еA, и выписать выражение для det е^А.

2) Пусть

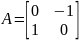
и Определить матрицу

9. 1) Пусть A, B . Какие должны быть выполнены условия, чтобы выполнялось соотношение

2) Использовать предыдущую формулу для доказа­тельства того, что е^А всегда имеет обратную.

10. Пусть A . След матрицы A (обозначается tr A) определяется по формуле

Если A — матрица с элементами

то, используя индукцию, показать, что

т. е. доказать, что в данном случае

det е^A = е^{tr А}.

11. Пусть A имеет собственный вектор х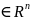 , соответствующий собственному значению R. Доказать, что х является собственным вектором е^А, со­ответствующим собственному значению .

12. 1) Доказать, что если A , то det A^-1 = (delA)^-1.

2) Доказать, что если A О(п), то det A = ± 1.

13. Доказать, что SO(2) является подгруппой O(2).