Глава 4. Основные понятия арифметики

Итак, мы определили операции и описали некоторые их свойства. Теперь посмотрим, что можно сделать с со­вокупностью операций, заданных на множестве.

Множество с заданными на нем операциями называ­ют алгебраической структурой. Некоторые из наиболее часто встречающихся алгебраических структур будут рассмотрены позднее. Прежде чем приступить к их рас­смотрению, посмотрим на арифметику с неформальной точки зрения. В большинстве случаев мы будем опу­скать формальные определения, делая ударения на «следствия из правил», даже в тех случаях, когда это приводит к необычным способам использования извест­ных символов, которые обычно используются для пред­ставления десятичных чисел.

§ 1. «Малая» конечная арифметика

Арифметику можно рассматривать как множество с двумя операциями, действующими подобно сложению и умножению. Ее можно изучать многими способами. Что­бы уяснить требования арифметической системы, при­мем конструктивное приближение и рассмотрим целые числа (0, 1, 2, ...) просто как символы. В дальнейшем будем рассматривать только конечную арифметику, в ко­торой используется лишь конечное множество чисел; вначале это множество будет небольшим. Подразумевает­ся, что если А ~ N_m, то требуется т различных симво­лов, при этом никакие комбинации символов не разреша­ются. Если используются только десятичные числа, то т ≤ 10. Поскольку все множества данного размера би­ективны, то можно рассматривать только множества N_m.

Для большей наглядности рассмотрим множество N₆. Для этого необходимо построить таблицы умножения и сложения. Множество N₆ достаточно велико для того, чтобы изучать свойства основной структуры. Можно подумать, что для этой цели более уместным является множество N₂, однако это не так. Начнём со сложения.

О перация сложения имеет единицу, которая обычно обозначается символом 0, однако . Поэтому будем использовать множество , которое более удобно. Очевидно, что . Поэтому можно работать с , не теряя никаких свойств. Таким образом, к настоящему моменту мы имеем соответствующую табл. 4.1.

Так как операция коммутативна, то таблица должна быть симметричной. Труднее обстоит дело с ассоциа­тивностью. Если мы хотим, чтобы операция была ассо­циативной, и требуем, как обычно, существования обрат­ных элементов по сложению, то любой элемент должен входить ровно один раз в каждую строку и каждый стол­бец. Поясним это высказывание.

Если а + b = а + с, то

— а + (а + b) = — а + (а + с),

(— а + а) + b =(— а + а) + с,

0 + b = 0 + с,

b = с.

Рассмотрим теперь операцию, определенную в табл. 4.2. Из трех возможностей для операции сложения на только удовлетворяет всем условиям, что выгля­дит несколько необычно. Операция не коммутативна, а в нарушен критерий «единственности результата». Как же построить соответствующую операцию, удовлет­воряющую всем обсуждаемым выше свойствам? Из дальнейшего изложения будет видно, что наиболее труд­но обеспечить выполнение свойства ассоциативности. В предложенной ниже процедуре мы используем ассоциативность как основной шаг построения, и, следовательно, это свойство будет выполняться автоматически.

Ш аг 1. Число 0 является единицей для операции сложения. Поэтому получаем табл. 4.3.

Шаг 2. Определим следующую строку таблицы, удов­летворяющую условию «единственности результата». Чтобы подчеркнуть используемую технику, специально выберем результат, который отличается от привычного.

В озьмём

Так как операция должна быть коммутативной, заполним соответствующий столбец табл. 4.4.

Шаг 3. Заполним другие клетки таблицы, используя ассоциативность. Проследим подробно за каждой де­талью:

Здесь мы использовали соотношения 2+1=0 и 0+x= x. Далее

3 + 3 = (1 + 1)+3 = 1+(1 + 3)=1 + 5 = 4 и т. д.

Т аким образом, на основе значений 1+ x получаем таблицу для операции + (табл. 4.5).

При выполнении процесса надо учитывать дополнительные ограничения на шаге 2. Значения в нулевой строке должны выбираться так, чтобы они «продолжали» все . Например, начиная с 1 (как мы делали), получаем

1 + 1 = 3, 3+1 = 5, 5+1 = 4, 4+1 = 2,

2 + 1 = 0, 0+1 = 1.

Следовательно, прибавляя только 1, можно получить все .

Перейдем теперь к умножению. Сначала заметим, что единица для операции умножения должна отличать­ся от нуля. В противном случае для любых х и у мы имели бы

, ,

поэтому

,

а значит, . Поэтому 0 не является единицей для умножения.

На самом деле нам требуется число, которое будет порождать . Следовательно, мы могли бы определить аналогичным образом операцию умножения на основе частичной табл. 4.6. Однако в этом случае мы не долж­ны настаивать па выполнении критерия «единственности результата». (В обычной арифметике не существует це­лого числа, которое при умножении на 2 давало бы 1! Поэтому в конечном множестве могут быть повторения.) Вместо того чтобы повторять процедуру построения таб­лицы для умножения, вернемся к проблеме связи двух операций — дистрибутивности умножения относительно сложения. Эта проблема связана с ассоциативностью. Рассмотрим (уже п остроенную) операцию сложения.

Заметим, что . Поэтому из предположения дистрибутивности получаем, что

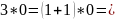
Теперь 3 + 3 = 4, 3+1=5, 1 + 4 = 2 и 1 + 2 = 0. Дей­ствуя, как и ранее, получаем следующую операцию (табл. 4.7).

Следовательно, начиная с почти произвольного выбо­ра строки в таблице, не содержащей 1 по сложению, и накладывая ряд простых ограничений, мы приходим к приемлемой арифметической системе. Теперь достаточно установить, что полученная система не находится в про­тиворечии с высказанными ранее соображениями, т. е. что 1 + 1 действительно существует. Короче говоря, если в нормальной (бесконечной) арифметике и , то хотелось бы, чтобы и в нашей арифметике ответ был с. Следовательно, мы пришли к выбору

Недостающим элементов должен быть 0, поскольку 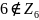, и 0 является единственным элементом , которого нет в строке. В результате такого выбора получаем соответствующую табл. 4.8. Она определяет так называе­мую арифметику по модулю 6. (Эта арифметика работа­ет точно так же, как и обычная целочисленная арифме­тика, за исключением того, что все целые числа заменя­ются па остатки от деления их на 6.)

У п р а ж н е н и е 4.1.

1. По аналогии с «естественной» арифметикой, полученной для , построить аналогичную арифметику для , используя символы

2. Построить арифметику для , которая согласуется со строкой

3. Р ассматривая , показать, что следующая таблица приводит к противоречию: