§ 6. Отношения на базах данных и структурах данных

Как уже установлено, все вокруг определяется отно­шениями. Достаточно лишь взять отношение s на пере­менных (x₁,…, x_n) так, чтобы можно было построить множество

{(х₁ х₂,…, х_n): s(x₁, х₂,…, х_n) истинно}.

Пусть задан набор (х₁,…, х_n). Отношение s(х₁,…, х_n) можно разрешить, т. е. выяснить, s(х₁,…, х_n) истинно или ложно. Конечно, s не обяза­тельно будет представлено «хорошей» формулой. Не­трудно показать, что вместо отношения s, определяюще­го множество наборов длины n, любое множество таких наборов также определяет отношение (и содержатель­ные свойства s). Эти два подхода эквивалентны.

Определение. При обработке данных наборы из n элементов называют записями; элементы этих набо­ров называют полями. Записи, определяющие отношение, обычно содержатся в файле. Если потребовать, чтобы несколько файлов содержали совокупность записей, удовлетворяющих некоторым отношениям, то мы полу­чим (относительную) базу данных.

Замечание. Для случая обработки данных мы сей­час употребили термин «поле». В гл. 5 мы будем упо­треблять этот термин в математическом смысле, однако в данном случае это не приводит к недоразумению.

Таким образом, это дает нам первый реальный при­мер отношений, которые в большей мере Связаны с вы­числениями, в частности, с прикладными задачами. Тем не менее краткое обсуждение некоторых простейших свойств баз данных не только обеспечивает основу даль­нейшего математического исследования отношений, но и проясняет некоторые факторы, понимание которых необ­ходимо для эффективного управления системами баз данных.

Современная теория баз данных включает в себя изучение так называемых нормальных форм, однако обо­снование некоторых из них очевидно лишь в простых случаях. Мы рассмотрим только три формы для следу­ющих задач:

• вставить новый набор из n элементов;

• удалить набор из n элементов;

• модифицировать набор, содержащий n элементов.

Начнем с простейшей нормальной формы.

Определение. Файлы в первой нормальной фор­ме (1NF), или — более просто — нормализованные фай­лы, имеют записи фиксированной длины, состоящие из элементов, взятых из множеств, чьи элементы далее не могут быть разбиты, и в каждый момент времени этот файл может быть представлен как массив значений М x N. Каждая запись, будучи набором из n элементов, может быть записана как строка массива. //

Пример 6.1. Рассмотрим отношение FAM1 (см. выше), в котором мы собрали вместе родителей и детей. Каждая запись содержит в указанном порядке фамилию и имена отца, матери и детей. Следовательно, мы имеем записи

(Смит, Джой, Джойс, (Сэлли, Бен)) FAM1,

(Браун, Фред, Лиза, (Люси)) FAM1.

Теперь, если мы обозначим через F и М множества от­цов и матерей, то из определения следует, что

Джой(Смит) F, Джойс (Смит) М,

Фред(Браун) F, Лиза (Браун) М.

Таким образом, Люси является членом семьи Браун, но Сэлли и Бен не являются детьми семьи Смит. Так как в этой семье более одного ребенка, то соответствующая запись больше, и, следовательно, нарушены условия пер­вой нормальной формы.

Из FAM1 мы можем получить отношение FAM2, по­строив его из S, F, М и C, где S — множество фамилий, а C — множество детей, путем конструирования записей:

(Смит, Джой, Джойс, Сэлли),

(Смит, Джой, Джойс, Бен),

(Браун, Фред, Лиза, Люси).

Отношение FAM2 находится в 1NF и может быть пред­ставлено при помощи табл. 2.1.

Таблица 2.1

Фамилия	Отец	Мать	Ребенок
Смит Смит Браун	Джой Джой Фред	Джойс Джойс Лиза	Сэлли Бен Люси

Однако не совсем ясно, что будет, если, например, супруги Джонс не имеют детей? Если мы хотим иметь в файле запись о них, то следует пересмотреть структу­ру файла. Это означает, что все следует начать сначала. Введем следующую терминологию.

Определение. При использовании таблицы для изображения отношения (файла с n-мерными набора­ми/записями, записываемыми в виде строк) столбцы на­зываются атрибутами. //

Следовательно, ФАМИЛИЯ, ОТЕЦ, МАТЬ и РЕБЕ­НОК являются атрибутами различных полей в FAM2. Для получения доступа к записям в файле используют­ся так называемые ключи. Более точно это может быть определено в терминах атрибутов.

Определение. Атрибут или (упорядоченное) множество атрибутов, чьи значения однозначно опреде­ляют запись в файле, называются ключом этого файла. (Заметим, что в файле может быть много различных ключей.) //

Каждый ключ отношения/файла FAM2 должен вклю­чать атрибут РЕБЕНОК.

Перейдем к другим примерам.

Пример 6.2. Каждый владелец компьютера дол­жен покупать к нему запасные части. Поэтому мы мо­жем рассмотреть файл, структура которого показана в табл. 2.2.

Таблица 2.2

КОМПАНИЯ	ОТДЕЛЕНИЕ	МЕНЕДЖЕР
АСЕ	LONDON	SMITH
IBL	LONDON	JONES
DATAMETZ	BIRMINGHAM	JONES
PRINTACO	MANCHESTER	BROWN
WOOLIES	BIRMINGHAM	BROWN
RTX	LONDON	SMITH
OXONDATA	OXFORD	WILSON

Атрибут КОМПАНИЯ является ключом в SUP1; вся другая информация в файле доступна при посредст­ве ключа. Таким образом, например, можно извлечь ат­рибут ОТДЕЛЕНИЕ при помощи ключа WOOLIES или же МЕНЕДЖЕР из RTX. //

Определение. Если запись локализована с по­мощью некоторого ключа, то поле, выделяемое из этой записи, называется проекцией. В данном контексте про­екцией является «из». Будем также говорить, что эти атрибуты зависят от ключа. //

Н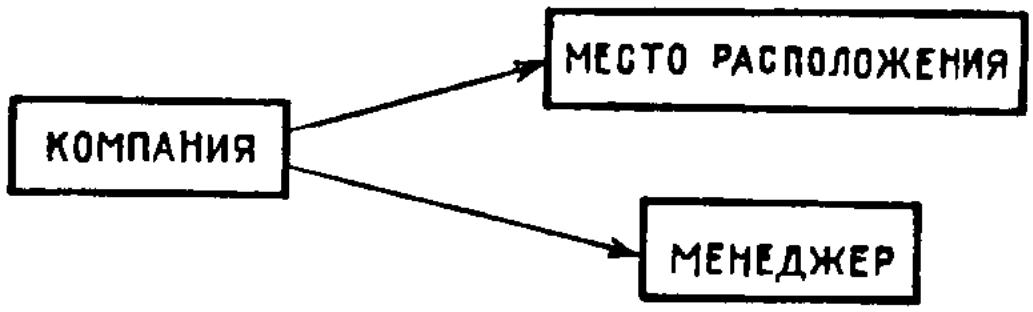 а рис. 2.7 представлен графический пример зависи­мостей в SUP1.

Рис. 2.7

Пример 6.3. Модифицируем файл SUP1 с целью включения туда информации об имеющихся на складе запасных частях и об их количествах, которые отдельный поставщик желает продать в отдельной сделке. Вклю­чим в файл также код поставки, из которого мы можем выяснить скорость и частоту поставок. Во избежание излишней детализации введены номер компании и номер запасной части (табл. 2.3). //

Таблица 2.3

КОМПАНИЯ	МЕСТО РАС­ПОЛОЖЕНИЯ	ПОСТАВЩИК	ЗАП. ЧАСТЬ	КОЛИЧЕСТ­ВО
1	LONDON	2	1	10
1	LONDON	2	2	1
1	LONDON	2	3	10
2	LONDON	2	2	2
2	LONDON	2	4	5
3	В'HAM	4	2	2
3	B'HAM	4	3	10
3	B'HAM	4	4	4
5	B'HAM	4	1	10
5	B'HAM	4	3	10
6	LONDON	2	1	10

Из табл. 2.3 выясним, какие преобразования мы мо­жем делать с SUP2, а какие нет:

а) вставка. Например, мы не можем добавить в файл запись, указывающую, что компания 4 (PRINTACO) находится в Манчестере, без указания деталей, которые она может поставлять;

б) удаление. Если компания 6 (RTX) прекратила поставки запчастей 1, тогда мы обязаны удалить все записи, относящиеся к этой компании и имеющие в поле ЗАП. ЧАСТЬ код 1;

в) модификация. Если код поставщика для Лондона изменился, например, из-за транспорта, то соответствую­щее поле должно быть изменено в каждой записи, где есть код LONDON в поле МЕСТО РАСПОЛОЖЕНИЯ.

Что можно сделать для того, чтобы уменьшить или отодвинуть эти проблемы? С практической точки зрения мы должны выделить информацию в SUP2 так, чтобы по возможности избежать повторений. Таким образом, мы получаем возможность вставки/удаления части запи­си в SUP2. Возможное и, на наш взгляд, разумное раз­деление дается в SUP3 (табл. 2.4). Тогда остаток ин­формации в SUP2 может содержаться в поле ЗАП.ЧАСТЬ. Используя эту конфигурацию, можно, например:

а) включить в SUP3 запись, означающую, что компа­ния 4 находится в Манчестере (код поставщика 3); б) удалить ссылку на компанию 6 как на поставщика запчасти 1, но оставить соответствующий код в SUP3;

в) изменить код поставщика для LONDON на 7 путем замены только трех входов, соответствующих компаниям с кодом 1, а не всех шести.

Результаты этих изменений приведены в табл. 2.5. Это уже значительно лучше, однако все же может быть еще усовершенствовано.

Таблица 2.4

Таблица 2.5

КОМ­ПА­НИЯ	МЕСТО РАСПОЛОЖЕНИЯ	ПОСТАВ­ЩИК
1	LONDON	7
2	LONDON	7
3	B'HAM	4
4	M'CHESTER	3
5	B'HAM	4
6	LONDON	7
ЗАП. ЧАСТЬ

КОМПАНИЯ	МЕСТО РАС­ПОЛОЖЕ­НИЯ	ПОСТАВ­ЩИК
1	LONDON	2
2	LONDON	2
3	B'HAM	4
5	B'HAM	4
6	LONDON	2
ЗАП. ЧАСТЬ

КОМПА-	ЗАП.	КОЛИ-
НИЯ	ЧАСТЬ	ЧЕСТВО
1	1	10
1	2	1
1	3	10
2	2	2
2	4	5
3	2	2
3	3	10
3	4	4
5	1	10
5	3	10

SUP3

КОМПА-	ЗАП.	КОЛИЧЕ
НИЯ	ЧАСТЬ	СТВО
1	1	10
1	2	1
1	3	10
2	2	2
2	4	5
3	2	2
3	3	10
3	4	4
5	1	10
5	3	10
6	1	10

Ч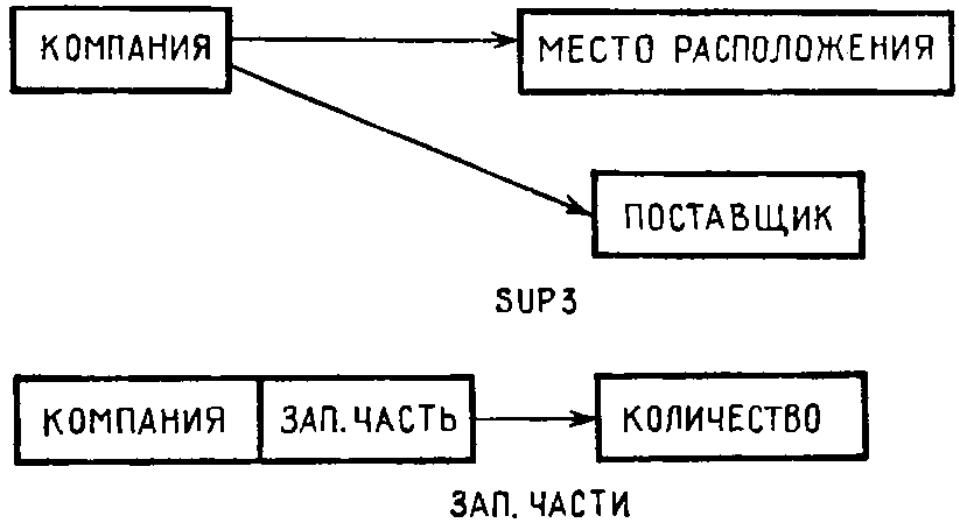 тобы увидеть, в каком направ­лении продолжать исследования, отделим ключи и под­чиненные части (рис. 2.8). Заметим, что ЗАП. ЧАСТЬ требует объединенного ключа.

Рис. 2.8

Все не-ключи непосредственно связаны с ключом. Это дает нам следующее свойство нормальной формы. /

Определение. Файл имеет вторую нормальную форму (2NF), если он имеет форму 1NF и неключевые атрибуты полностью независимы от ключа. /

Пример 6.3 (продолжение). Файл SUP3 все еще является достаточно сложным в том смысле, что для данной записи ПОСТАВЩИК может быть установлен при помощи исследования поля КОМПАНИЯ или же поля МЕСТО РАСПОЛОЖЕНИЯ. Это является причиной то­го, что в требовании а) код поставщика для Манчестера должен быть вставлен перед записью кода 4 компании, а требование б), возможно, потребует изменить более одной записи для модификации единственного поля дан-пых, относящегося к коду поставщика. На практике мы можем убрать эту проблему проектированием SUP3 в SUP4 и DEL (табл. 2.6). (Заметим, что коды поставщи­ка, изменяемые таким образом, препятствуют той воз­можности, что любые другие записи в файле вызывают противоречивую информацию. В SUP3 можно иметь за­пись вида «ПОСТАВЩИК КОМПАНИИ 6-2» и «ПОСТАВЩИК КОМПАНИИ 1-7» на некотором этапе мо­дификации SUP2, несмотря на тот факт, что обе компа­нии находятся в Лондоне.)

Зависимость отношений в SUP4 и DEL изображена на рис. 2.9. //

Нетранзитивность отношения зависимости является внутренним свойством, из которого возникает понятие третьей нормальной формы.

МЕСТО РАСПО­ЛОЖЕНИЯ	ПОСТАВЩИК
LONDON	7
B'HAM	4
M'CHESTER	3

Таблица 2.6

КОМПАНИЯ	МЕСТО РАСПО­ЛОЖЕНИЯ
1	LONDON
2	LONDON
3	B'HAM
4	M'CHESTER
5	B'HAM
6	LONDON

Определение. Файл находится в третьей нормаль­ной форме (3NF), если он является файлом 2NF, и каж­дый атрибут, не являющийся ключом, нетранзитивным образом зависит от ключа. / Возможен и другой путь — каждый атрибут, не яв­ляющийся ключом, зависит только от ключа и пи от че­го другого. Как было отмечено ранее, существует много других «нормальных» форм, но мы не ставим изучение файлов своей целью в дальнейшем. Достаточно лишь иметь в виду, что информация в файлах является о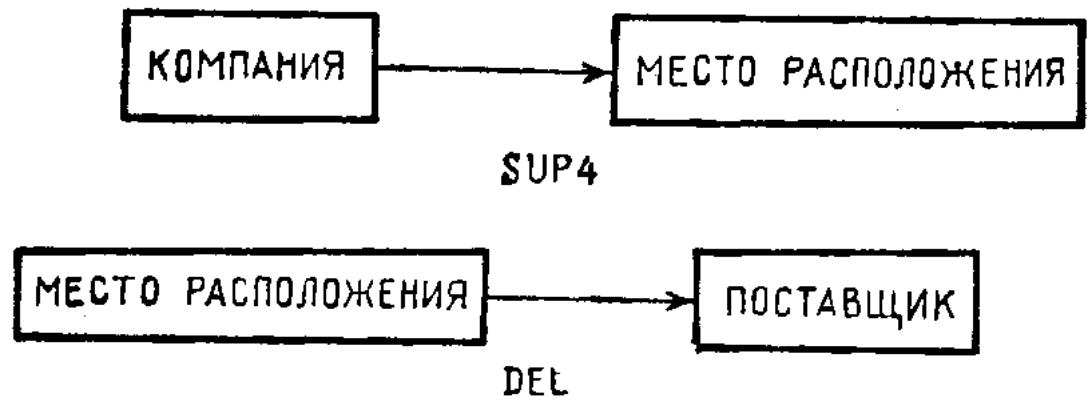 дной из реа­лизаций математического понятия отношения.

Рис. 2.9

Практическое использование отношений SUP4 и DEL требует явной связи атрибута МЕСТО РАСПОЛОЖЕ­НИЯ файла SUP4 с атрибутом МЕСТО РАСПОЛОЖЕ­НИЯ файла DEL. Это — отношение эквивалентности (между компонентами различных файлов, имеющих одно и то же имя). Подобные отношения эквивалентности мо­гут быть использованы для определения внутренних свя­зей и других структурных данных. В качестве иллюст­рации рассмотрим рис. 2.10. Диаграмма на рис. 2.10, a изображает дерево, диаграмма на рис. 2.10, b подобна диаграмме структурных данных, а диаграммы на рис. 2.10, c и d описывают их возможные применения. Отметим, что отношения эквивалентности различны, но результирующие структурные связи сохраняются. С ма­тематической точки зрения это является разбиением на классы эквивалентности. Следовательно, мы можем опре­делить произвольное представление этого дерева как эле­мент множества T = D/E, где

D = {a = (х, a, p), b = (y, b, z), с = (u, c, v), d = (q, d, r), e = (s, е, t)},

E = {(x, b), (y, d), (р, с), (z, e)}.

Эти вопросы будут обсуждаться в § 4 гл. 3.

Р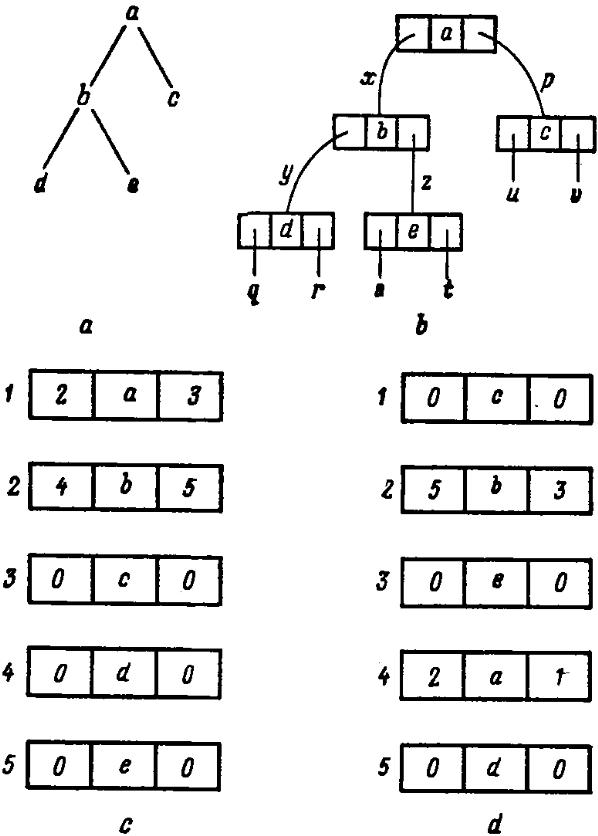 ис. 2.10