Тема 1. Случайные события. Элементы комбинаторики.

Комбинаторика – раздел математики, изучающий методы решения задач на подсчёт числа различных комбинаций. При решении комбинаторных задач применяют следующие правила.

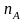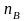Правило суммы (ИЛИ). Если некоторый объект А может быть выбран из совокупности объектов способами, а другой объект В может быть выбран из той же совокупности способами, то выбор одного из объектов А или В может быть осуществлён + способами.

Пример. В ящике 300 деталей. Известно, что 150 из них – 1-го сорта, 120 – 2-го, а остальные – 3-его сорта. Сколько существует способов извлечения из ящика одной детали 1-го или 2-го сорта?

Решение. Деталь 1-го сорта может быть извлечена 150 способами, 2-го сорта – 120 способами. Тогда 1-го или 2-го сорта: 150 + 120 = 270 способами.

Правило произведения (И). Если некоторый объект А может быть выбран из совокупности объектов способами, и после каждого такого выбора объект В может быть выбран способами, то выбор пары объектов А и В в указанном порядке может быть осуществлён способами.

Пример. В студенческой группе 25 человек. Сколько существует способов выбрать старосту и заместителя?

Решение. Старостой может быть выбран любой из 25 студентов, а его заместителем – любой из оставшихся 24 человек. Тогда общее число способов выбора старосты и заместителя: способов.

Выборки без повторений.

Пусть дано множество из n различных элементов. Из этого множества могут быть образованы подмножества из k элементов ( ).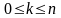

Размещениями из n элементов по k называют комбинации k элементов, составленные из n различных элементов, которые отличаются либо составом элементов, либо порядком их расположения.

Число размещений из n элементов по k обозначается 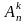и определяется формулой:

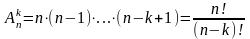
Пример. Расписание одного дня состоит из 5 пар. Определить число вариантов расписания при выборе из 11 дисциплин.

Решение.

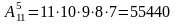
Если комбинации из n элементов по k отличаются только составом элементов, то их называют сочетаниями из n элементов по k. Обозначают 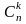и вычисляют по формуле:

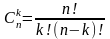
Пример. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Решение.

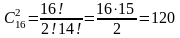
Свойства сочетаний.

1.

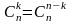
2.

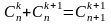
Перестановками из n элементов называют комбинации, составленные из n различных элементов, которые отличаются только порядком расположения этих элементов. Обозначают 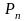, вычисляют:

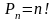
Пример. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьёвки при этом возможно?

Решение.

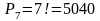
Из приведённых определений следует:

Выборки с повторениями.

Если в выборках (размещениях, сочетаниях, перестановках) некоторые из элементов (или все) могут оказаться одинаковыми, то такие выборки называются выборками с повторениями.

Число размещений из n элементов по k с повторениями равно:

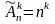
Пример. Сколько четырёхзначных чисел можно образовать из нечётных цифр, если цифры могут повторяться?

Решение. Нечётные цифры 1, 3, 5, 7, 9.

Тогда :

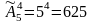
Число сочетаний из n элементов по k с повторениями равно:

Пример. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены одинаковые призы?

Решение. Так как призы одинаковые, то каждый из вариантов распределения призов представляет комбинацию 5 фильмов из 10, отличающуюся от других только составом фильмов, причём одни и те же фильмы могут повторяться. Тогда:

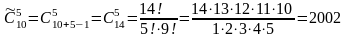
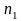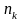Если в перестановках из общего числа n элементов есть k различных элементов, при этом 1-й элемент повторяется раз, 2-й - раз,…, k-й - раз, (причём + +…+ = n), то такие перестановки называют перестановками из n элементов с повторениями и вычисляют по формуле:

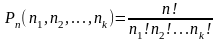
Пример. Сколько существует семизначных чисел, состоящих из цифр 4, 5 и 6, в которых цифра 4 повторяется 3 раза, а цифры 5 и 6 – по 2 раза?

Решение. Каждое семизначное число отличается от другого порядком следования цифр, то есть является перестановкой из 7 элементов с повторениями 3, 2 и 2. Тогда: