Тема: Регресійні моделі

1. Поняття регресії

Статистична залежність – це така залежність, за якої зміна однієї з величин викликає певний розподіл іншої величини.

Кореляційна залежність: зі зміною однієї з величин змінюється середнє значення іншої величини - розглядається умовне математичне сподівання, бо математичне сподівання характеризує середнє очікуване значення випадкової величини і називається функцією регресії y на x, де y - залежний фактор, або регресант, x- незалежний пояснюючий фактор, або регресор.

Якщо величина y залежить від одного фактора x, то цю залежність ми називаємо парною регресією: M( ) = f(x). Якщо умовне математичне сподівання залежить від багатьох факторів, то ми маємо множинну регресію: M( ) = f ( )

Регресія – це функціональна залежність між пояснювальними змінними і умовним математичним сподіванням залежної змінної, яка будується з метою його прогрозування для фіксованих значень незалежних факторів.

2. Причини наявності випадкового (стохастичного) фактора

При цьому реальні значення залежних змінних не завжди співпадають з УМС, тобто регресія обовязково містить випадкову величину, так званий стохастичний фактор и:

Y = M ( ) + u^{^}, Y = M ( ) + u^{^}.

Бажано, щоб значення u_i^{^} мали б нормальний закон розподілу N (0, ²).

Причини наявності випадкового (стохастичного) фактора:

1). Не включення до моделі всіх пояснюючих факторів.

2). Невірний вибір для розрахунків функціональної форми моделі y = ах + а_о, y = а_о х^а.

3). Агрегованість: пояснююча змінна є складною комбінацією інших факторів, які мають на неї певний вплив, крім тих факторів, що вже розглядалися в моделі.

4). Помилки вимірювання.

5). Обмеженість статистичних даних.

6). Непередбачуваність людського фактору.

3. Парна лінійна регресія

Парна лінійна регресія є найбільш розповсюдженою моделлю залежності між економічними змінними. Модель Кейнса – модель залежності окремого споживання С від наявного доходу І, де С₀ – це величина автономного споживання, в – гранична схильність до споживання ( від 0 до 1) : С = С₀ + b·І.

Д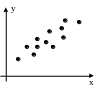 ля парної регресії за реальними статистичними даними будуємо кореляційне поле або поле розсіювання (хмара розсіювання) та висуваємо гіпотезу про можливий аналітичний зв’язок факторів моделі.

Х Y

x₁ y₁

x₂ y₂

... …

x_n y_n