- •Математика. Теория вероятностей и математическая статистика
- •Введение
- •Элементы комбинаторики
- •Классическое определение вероятности
- •Геометрическое определение вероятности
- •Случайные события. Действия над событиями
- •Теоремы сложения и умножения вероятностей
- •Формула полной вероятности. Формула байеса
- •Закон распределения дискретных случайных величин
- •Непрерывные случайные величины
- •Числовые характеристики случайных величин
- •Важнейшие распределения случайных величин
- •Методы статистического описания результатов наблюдений
- •Статистическое оценивание параметров распределения генеральной совокупности по выборке
- •Проверка статистических гипотез
- •Элементы теории корреляции и регрессионного анализа
- •Литература
- •Теория вероятностей и математическая статистика
- •302030, Г. Орел, ул. Московская,65
Непрерывные случайные величины
Непрерывной случайной величиной называется случайная величина, все возможные значения которой заполняют непрерывно конечный или бесконечный промежуток числовой прямой.
Интегральной
функцией распределения
случайной
величины
называтся
функция, которая для любого действительного
числа х
задает
вероятность того, что
![]() ,
т.е
,
т.е
![]() .
.
Случайная величина непрерывна, если ее интегральная функция распределения непрерывна на всей числовой прямой.
Плотностью
распределения вероятностей непрерывной
случайной величины или
дифференциальной функцией распределения
случайной величины называют
производную первого порядка от
интегральной функции распределения:
![]() .
.
Свойства плотности распределения:
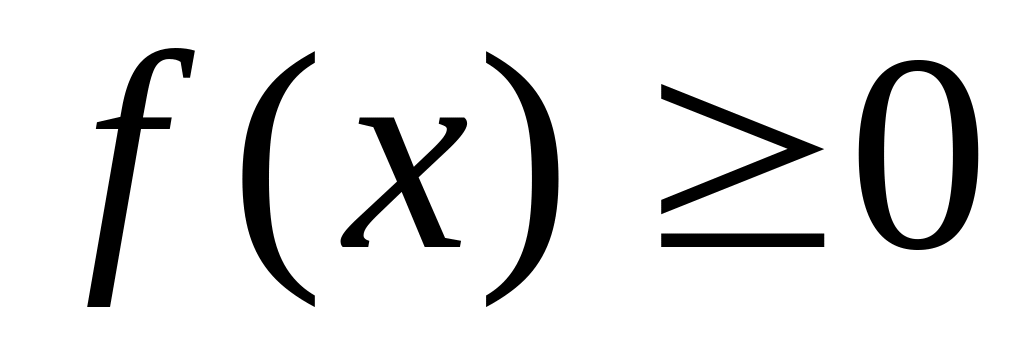 (
свойство неотрицательности);
(
свойство неотрицательности); (условие
нормировки);
(условие
нормировки); ;
;Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу
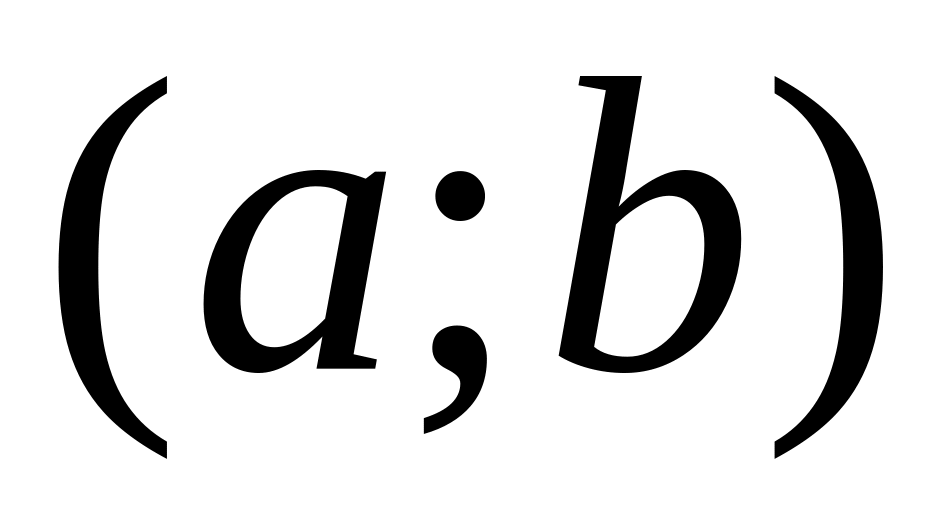 определяется
равенством
определяется
равенством

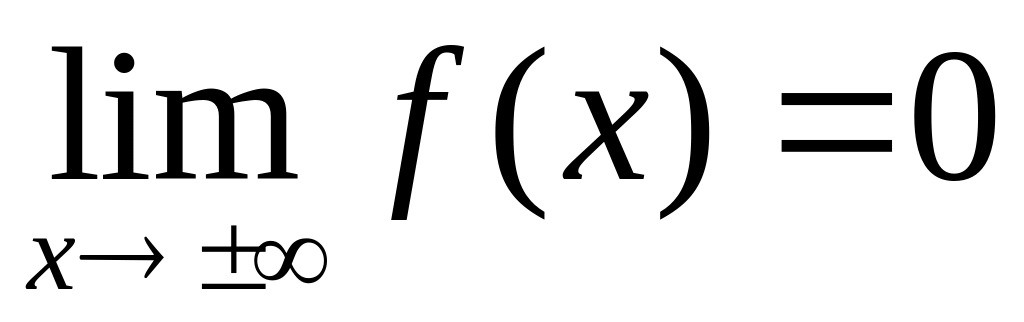
Задачи
Задана функция распределения н.с.в. :

Найти:
коэффициент с;
плотность распределения н.с.в.
 ;
;построить графики
 ;
; .
.
При каких значениях параметров k и b функция:

может
быть функцией распределения некоторой
непрерывной с.
в.
?
Найти вероятность того, что св.
примет
значение, заключенное в промежутке
![]() Построить график плотности
распределения этой случайной величины.
Построить график плотности
распределения этой случайной величины.
Задана функция распределения н.с.в. :
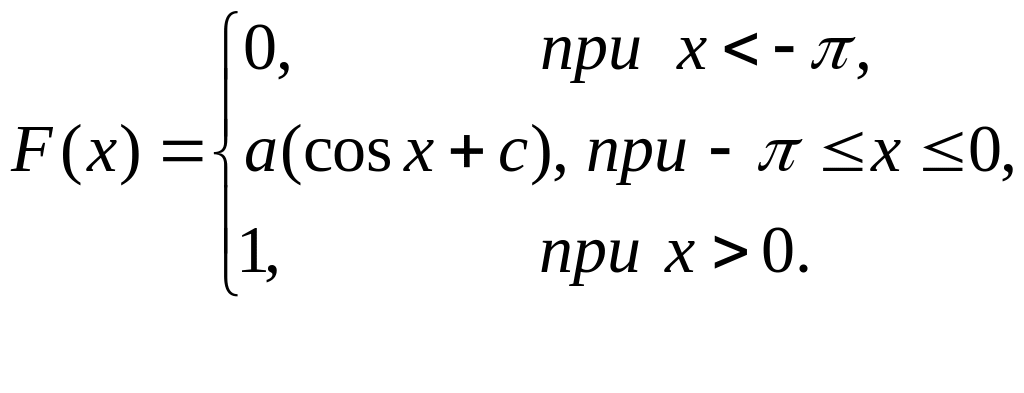
Найти:
коэффициенты а и с;
плотность распределения н.с.в. ;
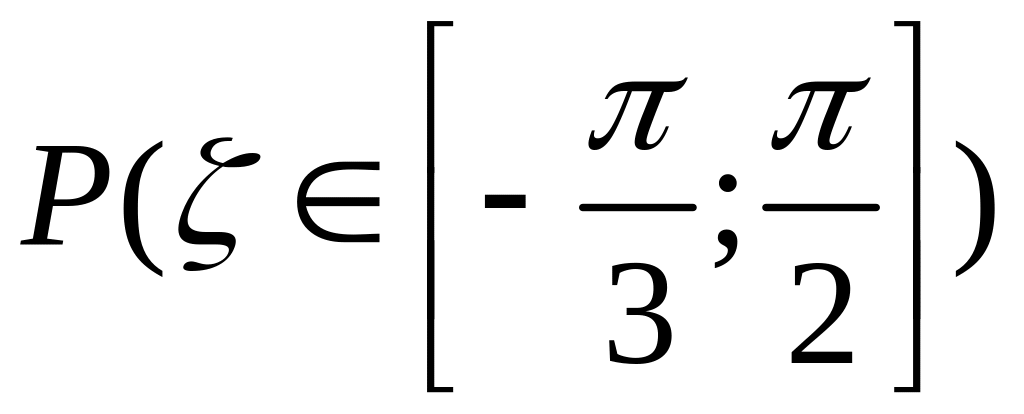 ,
,
 .
.
Задана функция распределения н.с.в. :

Найти:
коэффициенты А и В;
плотность распределения н.с.в. ;
 .
.
Задана функция распределения н.с.в. :
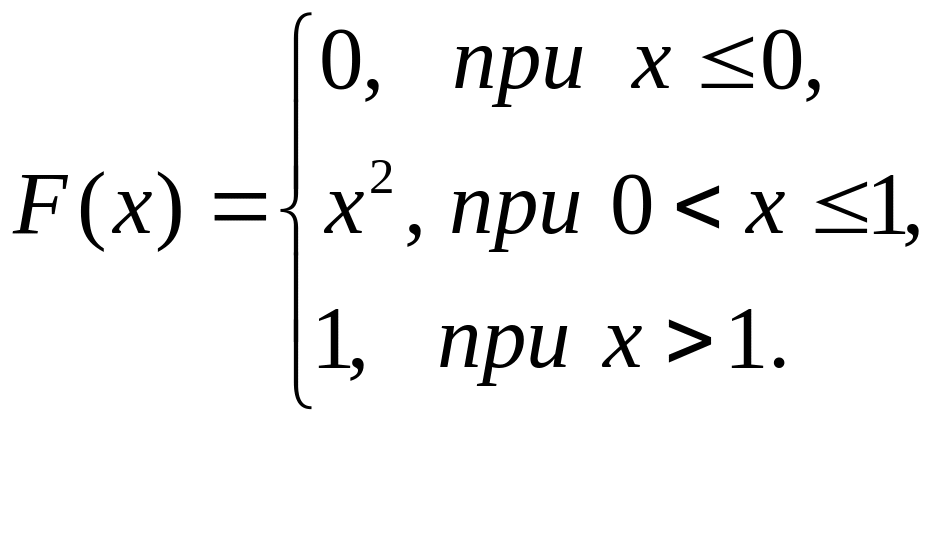
Найти вероятность
того, что в результате 4 независимых
испытаний эта величина ровно 3 раза
примет значение из промежутка
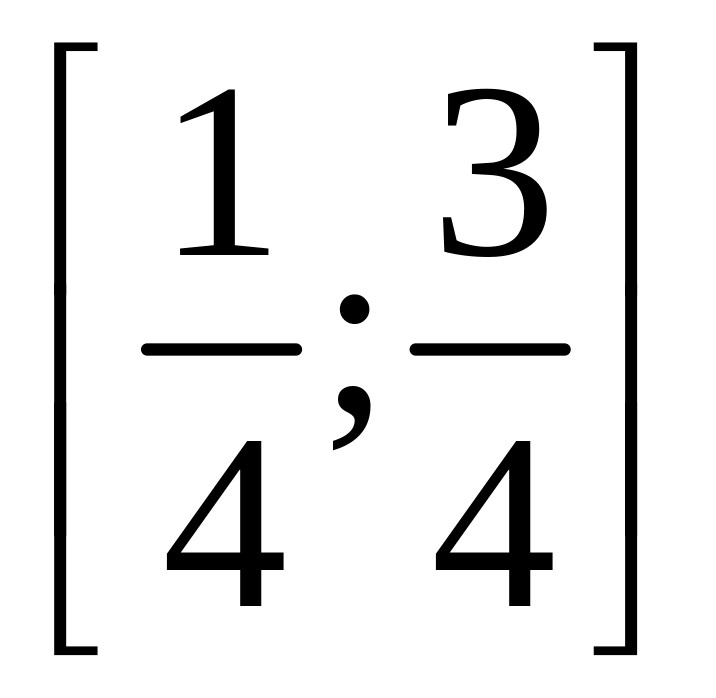 .
.
Задана дифференциальная функция распределения н.с.в. :
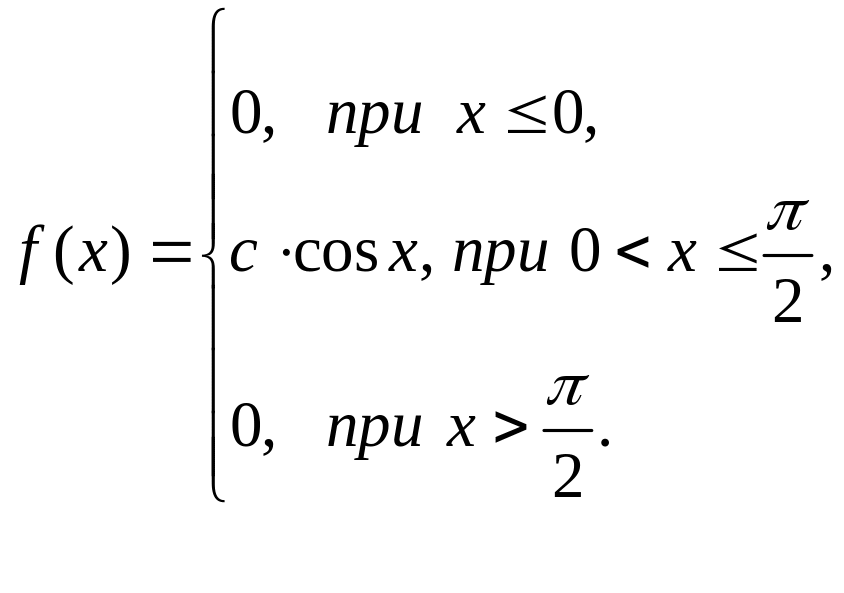
Найти:
коэффициент с;
интегральную функцию распределения н.с.в. ;
 .
.
Задана дифференциальная функция распределения н.с.в. :

Найти:
коэффициент а;
 .
.
Задана функция распределения н.с.в. :
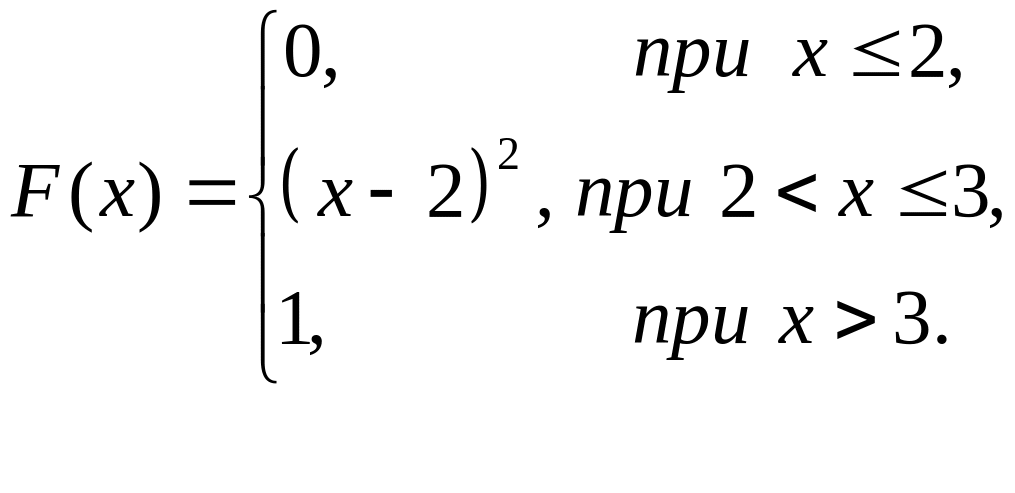
Найти:
плотность распределения н.с.в. ;
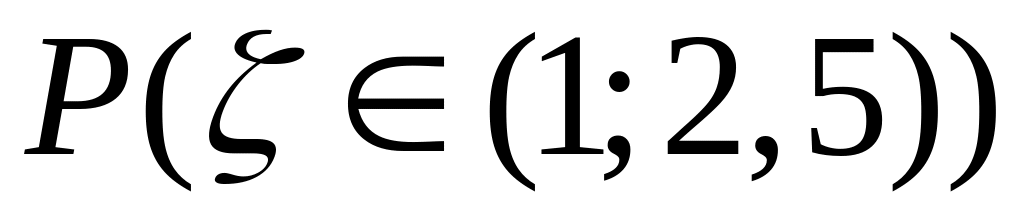 и
и
 .
.
Непрерывная случайная величина в интервале
 задана
плотностью распределения
задана
плотностью распределения
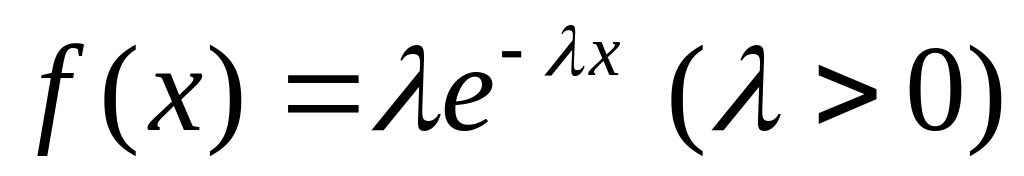 ;
вне этого интервала
;
вне этого интервала
 .
Найти вероятность того, что
примет значение, принадлежащее интервалу
(1;2).
.
Найти вероятность того, что
примет значение, принадлежащее интервалу
(1;2).
Числовые характеристики случайных величин
Математическое
ожидание дискретной
случайной величины –
это
сумма произведений всех ее возможных
значений на соответствующие им
вероятности, т.е.
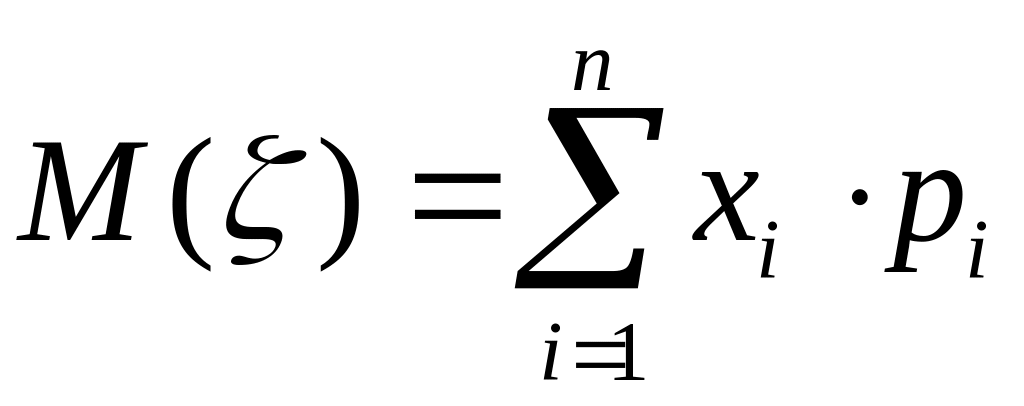 .
.
Математическое
ожидание непрерывной случайной величины
,
возможные значения которой принадлежат
всей оси
![]() ,
определяется равенством
,
определяется равенством
 .
.
В
частности, если все возможные значения
принадлежат интервалу
,
то
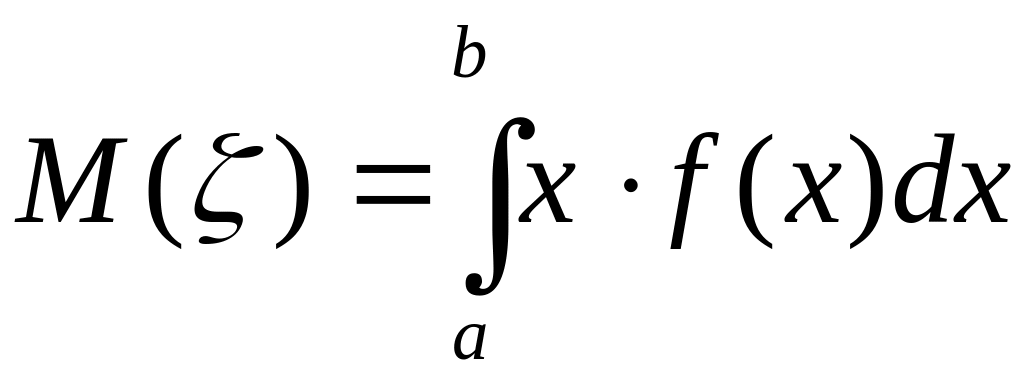
Дисперсия случайной величины – это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
![]() .
.
Дисперсия дискретной случайной величины вычисляется по формуле
 .
.
Дисперсию удобно вычислять по формуле
![]() .
.
Дисперсия непрерывной случайной величины , возможные значения которой принадлежат всей оси , определяется равенством
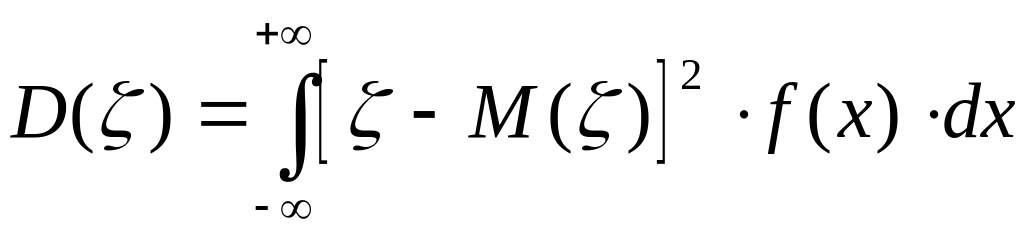
или равносильным равенством
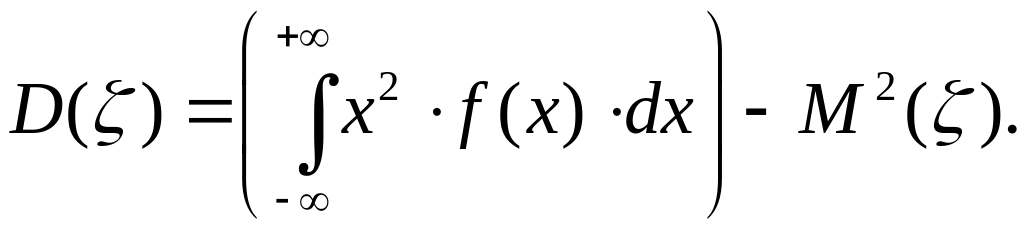
В частности, если все возможные значения принадлежат интервалу , то
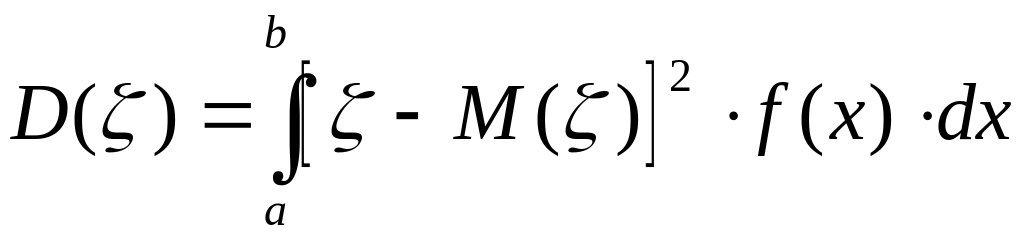
или
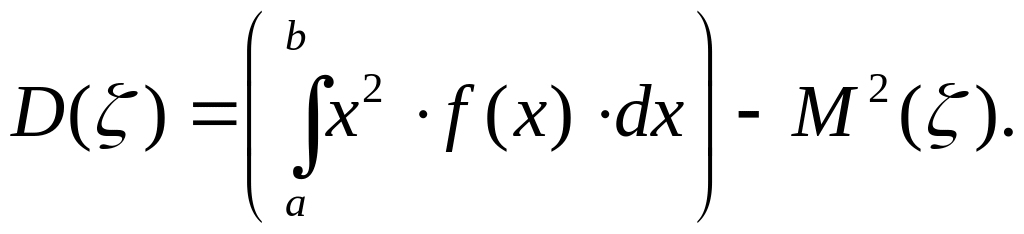
Среднее
квадратическое отклонение случайной
величины определяется
равенством
![]() .
.
Модой М0 ( ) непрерывной случайной величины называют возможное значение этой величины, которому соответствует локальный максимум плотности распределения.
Медианой
Ме
(
)
непрерывной случайной величины
называют возможное значение этой
величины, которое определяется равенством
![]() .
.
Начальным
моментом порядка k
случайной
величины
называют математическое ожидание
величины
![]() :
:
![]() .
.
В
частности, начальный момент первого
порядка равен математическому ожиданию:
![]() .
.
Центральный
момент порядка k
случайной
величины
называют математическое ожидание
величины
![]() :
:
![]() .
.
В частности, центральный момент первого порядка равен нулю:
![]() .
.
центральный момент второго порядка равен дисперсии:
![]() .
.
Задачи
Задан закон распределения д.с.в. :
|
-2 |
-1 |
0 |
1 |
2 |
3 |
|
0,1 |
0,2 |
0,25 |
0,15 |
0,1 |
0,2 |
Найти математическое
ожидание и дисперсию случайных величин
,
![]() ,
,![]() .
.
Задан закон распределения д.с.в. :
|
1 |
2 |
3 |
4 |
|
|
|
|
|
Найти
![]() ,
,
![]() .
.
Интегральная функция распределения д.с.в. имеет вид:
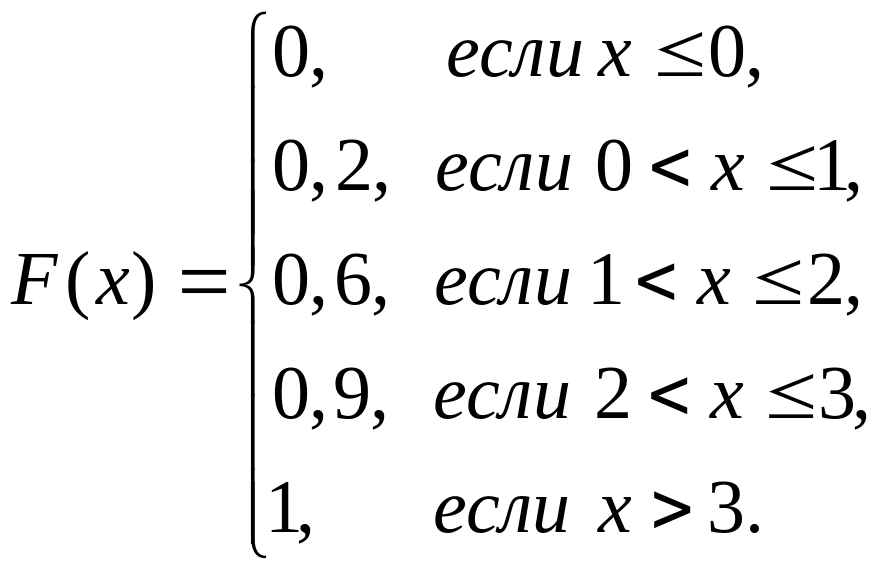
Найти
![]() .
.
Независимые случайные величины и заданы рядами распределения:
-
10
20
0.2
0.8
-
30
40
50
0,5
0,3
0,2
Найти
![]() двумя способами: 1) составив предварительно
ряд распределения для величины
двумя способами: 1) составив предварительно
ряд распределения для величины
![]() ;
2) используя правило сложения дисперсий.
;
2) используя правило сложения дисперсий.
Задана дифференциальная функция распределения н.с.в. :
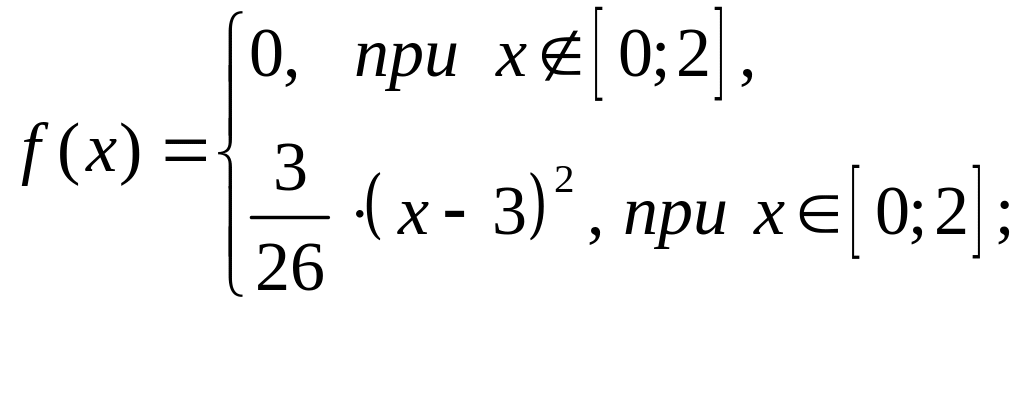
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
Задана функция распределения н.с.в. :
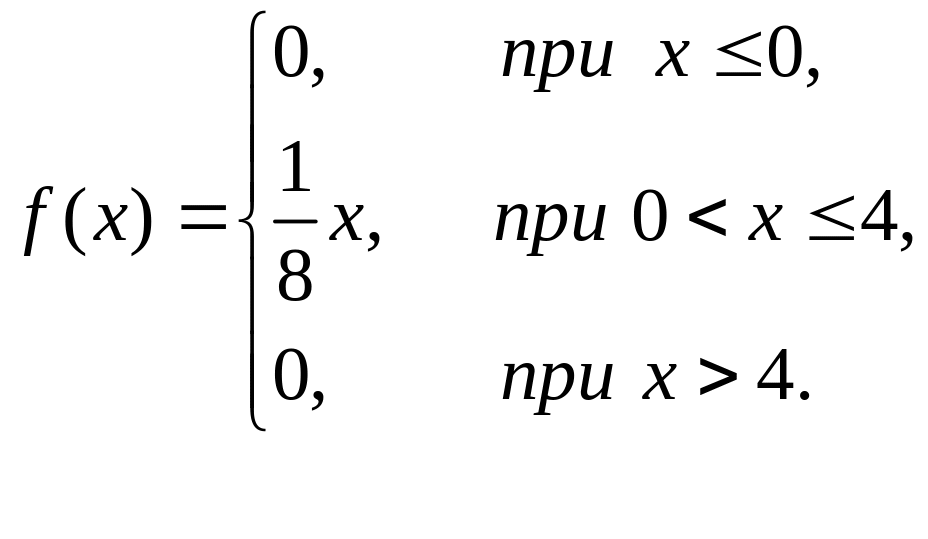
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
Задана дифференциальная функция распределения н.с.в. :

Найти моду и медиану.
Задана дифференциальная функция распределения н.с.в. :
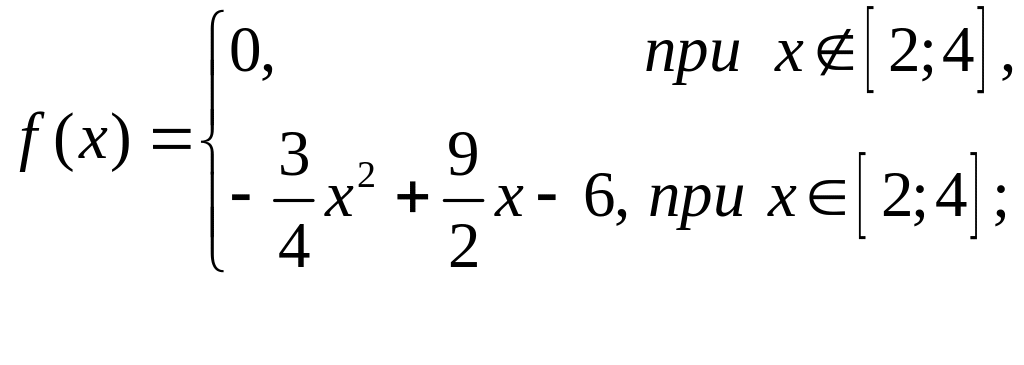
Найти математическое ожидание, моду и медиану.
Задана дифференциальная функция распределения н.с.в. :
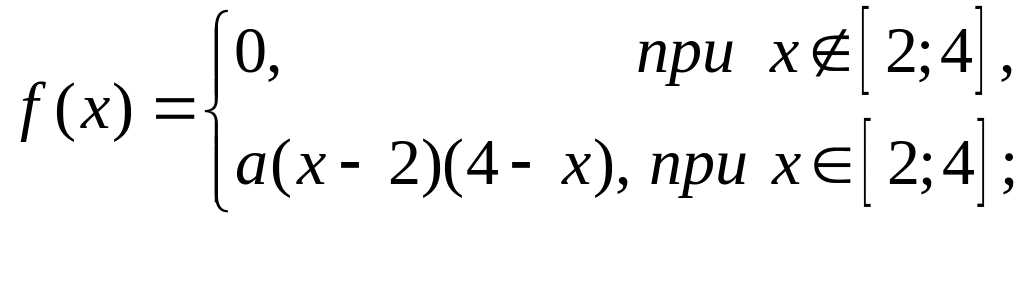
Найти значение параметра а, моду и медиану.
Трижды подбрасывается монета. С.в – число выпавших гербов. Составить закон распределения , найти начальные и центральные моменты первого и второго порядка, моду.
Используя условия задачи 8.6 найти начальные и центральные моменты первого и второго порядка.
Используя условия задачи 8.9 найти начальные и центральные моменты первого и второго порядка величин и .
Найти закон распределения дискретной случайной величины , зная, что она принимает два значения и
 и, кроме того,
и, кроме того,