14. Проверка статистических гипотез

Статистической гипотезой называется всякое высказывание о генеральной совокупности, проверяемое по выборке. Выдвигаемую гипотезу называют основной или нулевой гипотезой . Наряду с основной гипотезой выдвигают ей альтернативную . Если в ходе проверки отвергается основная гипотеза, то принимается альтернативная.

Статистическим критерием называется случайная величина с помощью которой принимают решение о принятии или отклонении гипотезы .

Для проверки гипотезы о виде распределения генеральной совокупности применяется критерий . Проверка гипотезы осуществляется по следующей схеме. По выборке находят оценки неизвестных параметров предполагаемого закона распределения случайной величины . Далее, область возможных значений случайной величины разбивается на интервалов , если – непрерывная величина, и на групп, состоящих из отдельных значений, если – дискретная величина. Используя предполагаемый закон распределения случайной величины , для каждого из этих интервалов находят вероятности того, что значение случайной величины принадлежит этому интервалу. Выборочное значение критерия вычисляется по формуле

.

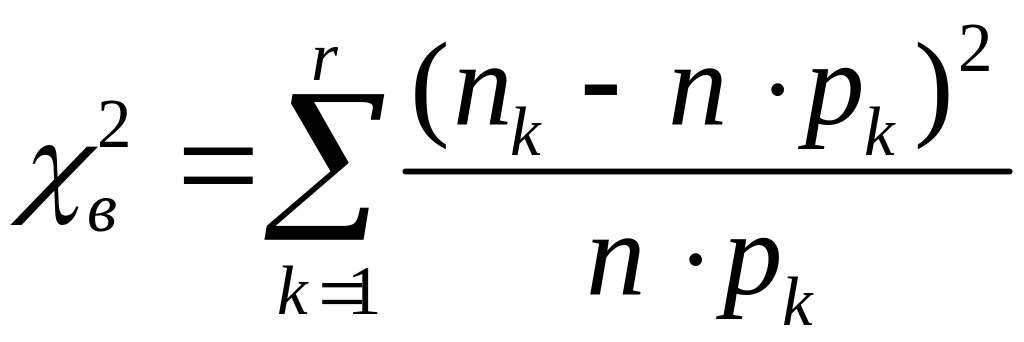Критическое значение критерия находят по таблице (приложение VII учебного пособия [10]), входами которой служат количество степеней свободы , где l – количество параметров распределения, оцениваемых по выборке, и уровень значимости , который задается исследователем.

Если , то гипотезу принимают на данном уровне значимости, если , то гипотезу отклоняют.

Задачи

1. В таблице приведены результаты измерения роста 1000 женщин в некоторой местности:

	<144	144- 147	147- 150	150- 153	153- 156	156- 159	159- 162	162- 165	165- 168	>168
	10	20	70	120	180	200	170	120	70	40

Проверить гипотезу о нормальном распределении.

2. Проверить гипотезу о равномерном распределении признака генеральной совокупности по результатам выборки:

   	2-4	4-6	6-8	8-10	10-12	12-14	14-16	16-18	18-20	20-22
   	21	16	15	26	22	14	21	22	18	25

3. Проверить гипотезу о распределении признака генеральной совокупности по закону Пуассона по результатам выборки( ):

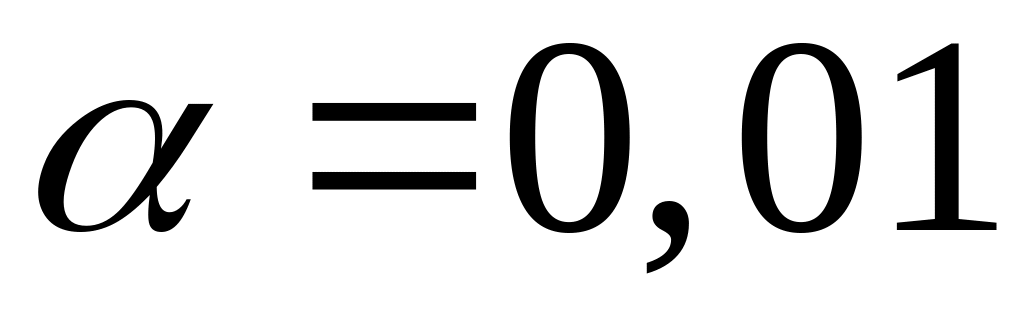a)		0	1	2	3	4
		116	56	22	4	2

б)		0	1	2	3	4
		129	73	65	2	1

в)		0	1	2	3	4
		161	82	53	8	4

4. Проверить гипотезу о нормальном распределении выборки из №12.2(б). Взять .

5. В таблице представлены результаты измерения контрольного размера деталей:

	2,9-3,9	3,9-4,9	4,9-5,9	5,9-6.9	6.9-7.9
	5	15	23	19	6

Проверить гипотезу о нормальном распределении выборки ( ).

6. В таблице представлены результаты измерений входного сопротивления 130 электронных ламп:

	3,0-3,6	3,6-4,2	4,2-4,8	4,8-5,2	5,2-5,8	5,8-6,4	6,4-7,0
	2	3	35	43	22	15	5

Проверить гипотезу о нормальном распределении выборки ( ).