3. Інтегрування диференціального рівняння обертального руху твердого тіла навколо нерухомої осі

3.1. Це рівняння має вигляд (3.1)

і по своїй структурі аналогічне основному рівнянню динаміки в проекції на будь-яку вісь (1.1). В ньому роль маси відіграє момент інерції l_z, прискорення - кутове прискорення , а суми сил - сума моментів зовнішніх сил відносно осі обертання. Таким чином за допомогою рівняння (3.1) можна розв'язувати як прямі, так і обернені задачі динаміки обертального руху тіла навколо нерухомої осі (див.п.п. 1.1 ... 1.4).

3.2. Порядок розв'язання задач динаміки обертального руху твердого тіла навколо нерухомої осі така:

- вибрати осі координат і задати напрям однієї з них (осі Z) уздовж осі обертання твердого тіла;

• зобразити на розрахунковій схемі всі зовнішні сили, що діють на систему, включаючи реакції в'язей;

• обчислити суму моментів усіх зовнішніх сил відносно осі обертання, враховуючи, що знак "+" у моменту береться тоді, коли його напрям збігається з напрямком обертання тіла і знак "-" - коли не збігається;

• дослідити розв'язок, щоб визначити область його застосування.

3.3. При обчисленні моментів інерції, що містяться в рівнянні (3.1), слід мати на увазі теорему про паралельний перенос, за якою визначають моменти інерції відносно паралельних осей:

, (3.2) (3.35)

l_zc- центральний момент інерції: вісь Z_c проходить через центр мас С;

l_z - момент інерції відносно осі Z , яка паралельна осі Z_c;

d - віддаль між осями; М - маса тіла.

13

Перш ніж користуватися теоремою (3.2) треба добре розібратися в обчисленні моментів інерції для простих фігур (кільце, прямокутник, трикутник , круг тощо) [1,2]. Суттєву допомогу при розв'язанні практичних задач надають табл. 2.4 [7] або табл. 46 [4].

П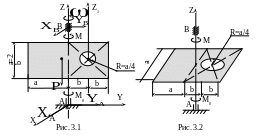 риклад 3.1. Однорідна пластинка товщиною м , яка виготовлена з матеріалу густиною 8000 кг/м³, має вертикальну вісь обертання і приводиться в рух зі стану спокою ( 0) парою сил з моментом М= 100 Нм (рис. 3.1). При обертанні на пластинку діють сили опору, момент яких відносно осі обертання дорівнює Нм. Знайти закон обертального руху пластинки , якщо а = 0,4 м, b = 0,2м.

Розв'язання. Вибираємо початок координат в нижній опорі А і напрямляємо вісь Z уздовж осі обертання пластинки. Зображаємо всі зовнішні сили, що діють на тіло: - сила тяжіння пластини; М - пара сил, М₀ - момент сил опору; , , , , - складові опорних реакцій. Для розв'язання задачі застосуємо рівняння (3.1), де ; . Маємо:

або , звідcи після інтегрування

. (3.3)

Для знаходження С₁ використаємо початкові умови задачі:

при t = 0 . З (3.3) при t = 0 маємо ,

тоді і , де k =5t/l_Z;

14

звідси

або .

Розділяємо змінні і інтегруємо

.

При t=0 , тому і маємо

. (3.4)

Для отримання кінцевого розв'язку обчислимо момент інерції пластинки (рис.3.1) відносно осі Z:

, (3.5) (3.38)

де значення та легко обчислюються за допомогою табл. 2.4 [7]:

,

.

Обчислимо маси прямокутної пластинки та кругового отвору :

, .

Таким чином маємо:

(кгм²).

Підставляючи в (3.4) значення , остаточно маємо

(рад). (3.6)

Зауваження. Якби нам необхідно було б розв'язати приклад 3.1 для схеми, яка зображена на рис. 3.2, то весь хід розв’язання залишився би без змін, лише складові в виразі (3.5) набули б нових значень у відповідності з табл. 2.4 [7]:

,

,

(кгм²).

Відповідь в цьому випадку набуває (3.2) вигляду

(рад).

Відповідь: пластинка обертається за законом

(рад) для рис.3.1.

(рад) для рис.3.2;

15