Решение

1. Для генеральной средней

_мв= t_мв

n = 10

S² = ((1450-1370)² + (1370-1370)² + (1250-1370)² + … + (1430-1370)²) : (10-1) = 3620

Для определения t исчислим S_t

K = n-1 = 10-1 = 9

По таблице распределения Стьюдента при S_t = 0,985 и К = 9 коэффициент доверия t = 2,6

1317,8 1422,2 (час.)

Следовательно, с вероятностью 0,97 можно утверждать, что генеральная средняя колеблется в пределах от 1317,8 до 1422,2 часа.

2. Для определения вероятности того, что отклонение генеральной средней от выборочной средней не превышает 48 часов, имеем следующие данные: _мв = 48 час _мв = 20,06 (см. п.1).

Отсюда t фактическое =

Пользуясь таблицей распределения Стьюдента, определяется значение функции S_t при t = 2,4 и К = 9.

S_t = 0,98

Вероятность того, что отклонение генеральной средней от выборочной средней не превзойдет 48 час.

P = 2 S_t – 1 = 2*0,98 – 1 = 0,96

Вероятность того, что ошибка будет превышать 48 час.

P = 1-0,96 = 0,04

Таким образом, вероятность того, что средней срок службы ламп для всей партии отличается от полученного по выборке не более чем на 48 часов, равна 0,96 или 96%, а вероятность того, что средний срок службы будет отличаться от выборочного более, чем на 48 часов, равна 0,04 или 4%.

3.Типическая выборка

В составе генеральной совокупности с различным уровнем изучаемого

признака более равномерное представительство в выборочной совокупности различных типов обеспечивает типическая (расслоенная, районированная или стратифицированная) выборка.

При типической выборке неоднородная генеральная совокупность подразделяется на более однородные в отношении изучаемого признака группы (типы, районы). По каждой группе определяются объем в генеральной совокупности ( ) и число подлежащих наблюдению единиц в выборочной совокупности ( ). Отбор обследуемых единиц из генеральной совокупности в выборочную производится в каждой группе при помощи повторного либо бесповторного случайного отбора .

Общее число единиц выборочной совокупности (n) распределяется между группами пропорционально численности групп в составе генеральной совокупности (N). Такой отбор называется пропорциональным. Таким образом,

Формулы для расчета ошибок типический выборки приведены в таблице 2.

В таблице 2 - средняя из внутригрупповых дисперсий в выборочной совокупности

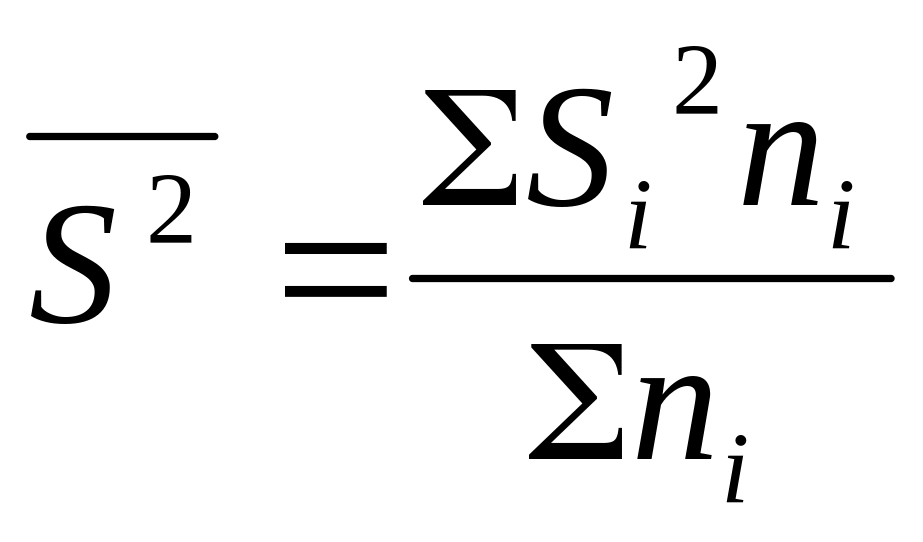
Таблица 2 – Формулы ошибок типической выборки

	Способ отбора единиц
	повторный	бесповторный
Средняя ошибка для определения средней при пропорциональном размещении единиц. Средняя ошибка для определения доли при пропорциональном размещении единиц

Величина ошибки типической выборки зависит от величины внутригрупповых дисперсий. Из правила сложения дисперсий следует, что ошибка типической случайной выборки меньше, чем ошибка простой случайной выборки.

Предельная ошибка типической выборки:

Приведем пример расчетов генеральных характеристик при типическом отборе.

Операция дискования при обработке почвы проводится в ОАО «Маяк» на трех тракторах. Для определения процента некачественно выполненного дискования проведена расслоенная (типическая) 10%- ая выборка. На первом тракторе было обработано 170 гектаров, на втором – 200 гектаров, на третьем – 180 гектаров. Количество некачественно обработанной площади в выборочной совокупности по первому трактору – 2, по второму - 3, по третьему – 3 гектара.

Определить: 1) интервалы, в которых с вероятностью 0,95 заключен процент некачественно обработанной площади в общей площади, подвергшейся дискованию; 2) вероятность того, что процент брака для всей обработанной площади отличается от полученного по выборке не более, чем на 1%.

Решение:

1. Общий объем генеральный совокупности

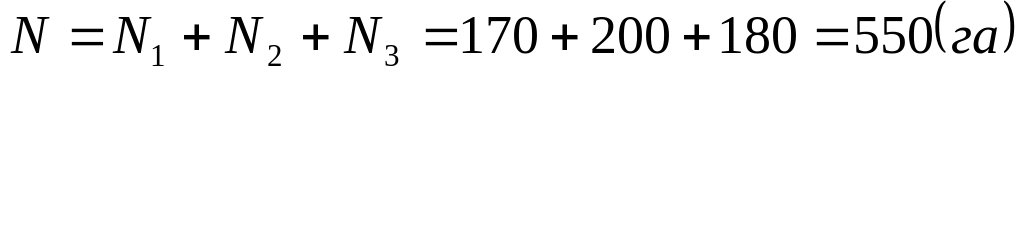
Численность выборки

Численность выборки по тракторам ,

т.е. для первого – 17(га)

для второго – 20(га)

для третьего – 18(га)

Доверительный интервал процента некачественно обработанной площади для всей совокупности (5500га)

или 0,2%

При вероятности p = 0,95 t = 1,96 (см. таблицу функции Лапласа)

14,5-0,94 ≤ P ≤ 14,5+0,94

13,56% ≤ P ≤ 15,44%

С вероятностью 0,95 можно утверждать, что процент некачественно обработанной площади в общей площади, продискованной тракторами, будет находиться в пределах от 13,56% до 15,44%

2. Известно, что =1% или 0,01

, следовательно,

( см. n.1)

Если t = 5, то ей соответствует вероятность р=0,999 (см. таблицу функции Лапласа).

Таким образом, вероятность того, что процент брака для всей обработанной площади отличается от полученного по выборке не более, чем на 1%, очень высока и достигает 0,999 (т.е. в 99,9% из 100%)