§ 82. Пучок плоскостей

Собственным пучком плоскостей называется множество всех плоскостей, проходящих через одну прямую.

Несобственным пучком плоскостей называется множество все параллельных между собой плоскостей.

Теорема 1. Для того чтобы три плоскости, заданные общими уравнениями

,

, (1)

относительно общей декартовой системы координат, принадлежали одному пучку, собственному или несобственному, необходимо и достаточно, чтобы ранг матрицы

был равен или двум, или единице.

Доказательство необходимости. Пусть три плоскости (1) принадлежат одному пучку. Требуется доказать, что

Предположим сначала, что три данные плоскости принадлежат собственному пучку. Тогда система (1) имеет бесконечное множество решений (т.к. по определению собственного пучка: три плоскости принадлежат пучку, если они проходят через одну прямую); это будет тогда и только тогда, когда , так как если , то система (1) или имеет единственное решение, или несовместна, смотря по тому будет ли определитель, составленный из коэффициентов при неизвестных, отличен от нуля или равен нулю.

Если три данные плоскости принадлежат несобственному пучку то ранг матрицы

равен 1, а значит, ранг матрицы М равен или двум или единице.

Доказательство достаточности. Дано: Требуется доказать, что три данные плоскости принадлежат одному пучку.

Если , то и . Пусть . Тогда система (1) совместна, имеет бесконечное множество решений, а среди данных плоскостей есть пересекающиеся, (т.к. если бы не было пересекающихся, то они были бы все параллельны и ранг матрицы был бы равен 1), поэтому три данные плоскости принадлежат собственному пучку.

Если ; , то все плоскости коллинеарны (две из них непременно параллельны, а третья может и совпадать с одной из параллельных плоскостей).

Если , то и , и все плоскости совпадают.

Теорема 2. Пусть в общей декартовой системе координат заданы две различные плоскости и общими уравнениями: ; .

Для того, чтобы третья плоскость , заданная также общим уравнением

относительно той же системы координат, принадлежала пучку, определяемому плоскостями и , необходимо и достаточно, чтобы левая часть уравнения плоскости была линейной комбинацией левых частей уравнений плоскостей и .

Доказательство необходимости. Дано: плоскость принадлежит пучку плоскостей, определяемому плоскостями и . Требуется доказать, что существуют числа и , такие, что будет выполнено тождество, справедливое при всех значениях х, у, z:

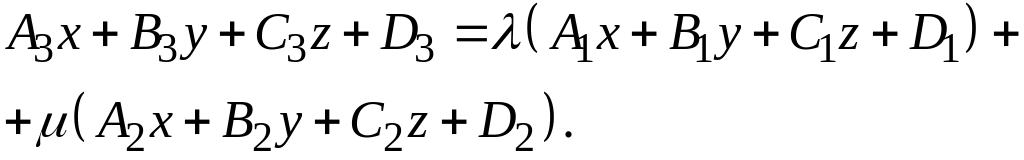В самом деле, если три плоскости , и принадлежат одному пучку, то , где

.

Первые две строки этой матрицы линейно независимы (поскольку плоскости и различны), а так как , то третья строка есть линейная комбинация двух первых, т.е. существуют число и , такие, что

Умножая обе части первого равенства на х, обе части второго на у, обе части третьего на z и складывая почленно полученные равенства и равенство , получим доказываемое тождество.

Доказательство достаточности. Пусть тождество

справедливо при всех значениях х, у и z. Требуется доказать, что плоскость принадлежит пучку, определяемому плоскостями и .

Из данного тождества следуют соотношения ,

,

,

,

так что третья строка матрицы М есть линейная комбинация двух первых, а потому . Ч.т.д.

Уравнение где и не равны нулю одновременно, называются уравнением пучка плоскостей, определяемого двумя различными плоскостями и , уравнения которых в общей декартовой системе координат таковы:

, (3)

Как было доказано, уравнение всякой плоскости пучка, определяемого различными плоскостями и , может быть записано в виде .

Обратно если уравнение , в котором хотя бы одно из чисел и не равно нулю, есть уравнение первой степени, то оно является уравнением плоскости, принадлежащей пучку, определяемому плоскостями и . В самом деле, третья строка матрицы М, составленной из коэффициентов уравнений и имеет вид

,

т.е. является линейной комбинацией двух других, поэтому .

Если плоскости и пересекаются, а и не равны нулю одновременно, то все коэффициенты при х, у, z в уравнении не могут быть равны нулю, так как если бы имели место соотношения

,

то плоскости и были бы коллинеарны вопреки предположению.

Но если плоскости и параллельны, то существуют такие числа и , среди которых хотя бы одно не равно нулю, и такие, что в уравнении все коэффициенты при х, у и z равны нулю. Но тогда это будет несобственный пучок, и также как и в случае пучка прямых, здесь надо быть очень внимательным.