Лекция 12.

§ 77. Уравнение прямой в пространстве, проходящей через данную точку в данном направлении. Параметрическое уравнение прямой

Теорема 1. В общей декартовой системе координат уравнения прямой, проходящей через точку и имеющей направляющий вектор , будет иметь вид

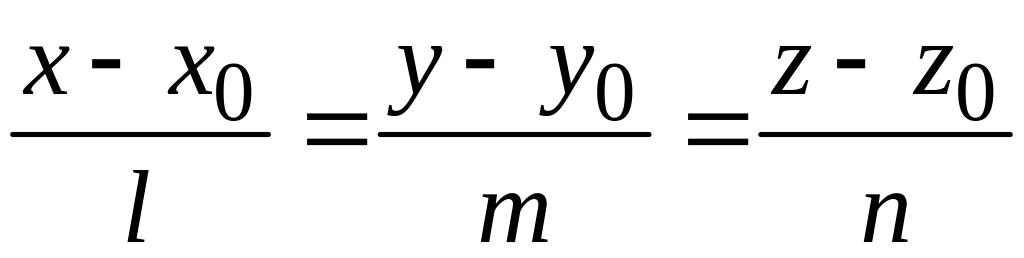(1)

(эти уравнения называются каноническими уравнениями прямой), или в параметрической форме

(2)

или в векторно-параметрической форме

.

Доказательство. Пусть М (х, у, z) – произвольная точка; она лежит на прямой, проходящей через точку , коллинеарной вектору тогда и только тогда когда векторы и коллинеарны, т.е. тогда и только тогда, когда координаты этих векторов пропорциональны:

.

Так как , то необходимое и достаточное условие коллинеарности векторов и можно записать еще и так:

,

или

,

о тсюда сразу получаются параметрические уравнения (2) прямой

Соотношение

эквивалентно такому:

,

где - радиус-вектор точки , - радиус-вектор точки М. Из последнего уравнения находим

.

Параметр t есть координата точки М данной прямой в следующей системе координат на этой прямой: начало координат, - масштабный вектор.

§ 78. Уравнения прямой, проходящей через две точки

Уравнения прямой, проходящей через две различные точки и , заданные относительно общей декартовой системы координат, можно записать в виде

,

или в параметрической форме

Доказательство. За направляющий вектор прямой можно взять вектор , после чего остается применить результаты теоремы 1.

§ 81. Прямая как линия пересечения двух плоскостей

В общем случае прямую р в общей декартовой системе координат можно задать уравнениями двух плоскостей:

пересекающихся по этой прямой.

Для приведения прямой, заданной двумя пересекающимися плоскостями и к каноническому виду надо найти какое-нибудь решение системы , . Точка лежит на прямой, по которой пересекаются плоскости и . Далее вектор с координатами

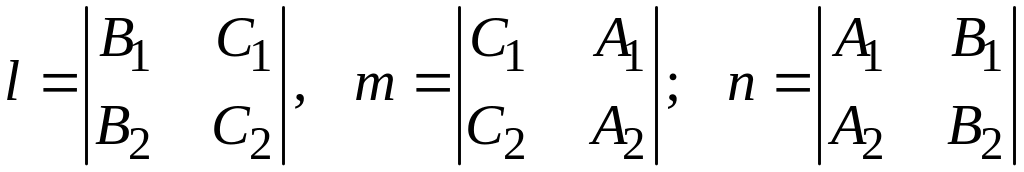
является направляющим вектором данной прямой, так как он ненулевой и компланарен каждой из данных плоскостей. В самом деле, применяя необходимое и достаточное условие компланарности вектора и плоскости, получим

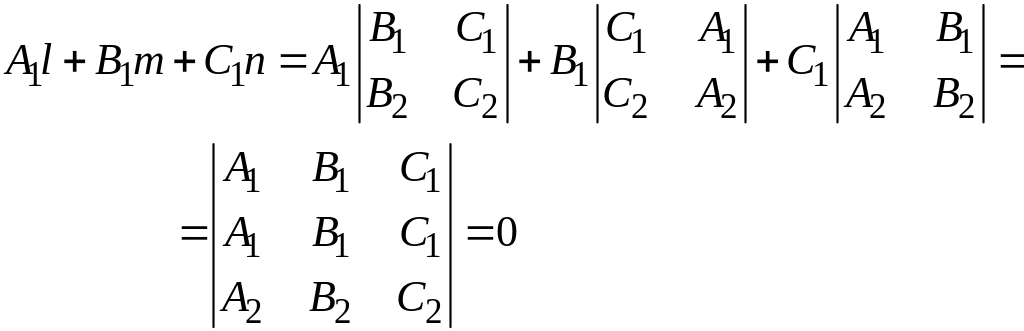
и аналогично , так что вектор коллинеарен прямой, по которой пересекаются плоскости и . Каноническое уравнение этой прямой можно записать в виде

.

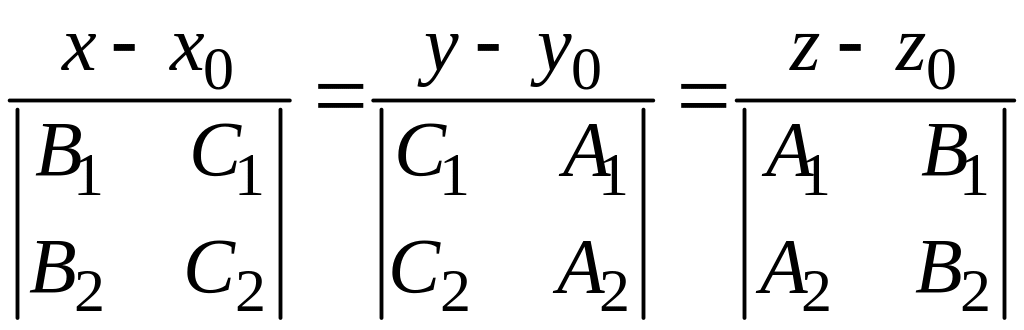§ 85. Геометрический смысл неравенства первой степени с тремя неизвестными

Теорема 2. Пусть относительно общей декартовой системы координат задана плоскость общим уравнением

(1)

Тогда для координат х, у, z всех точек , лежащих по одну сторону от плоскости , выполняется неравенство

,

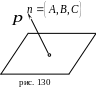а для координат х, у, z всех точек лежащих по другую сторону от плоскости , - неравенство . Плоскость делит пространство на два полупространства. То полупространство, для координат всех точек которого

,

будем называть положительным, а другое, для координат всех точек которого , отрицательным.

Теорема 3. Пусть относительно общей декартовой системы координат плоскость задана общим уравнением

.

Тогда, если отложить главный вектор этой плоскости от любой точки этой плоскости , то конец Р отложенного вектора будет находится в положительном полупространстве от данной плоскости (рис. 130).

Теорема 2 и 3 доказываются аналогично тому, как были доказаны теоремы 1 и 2 в § 62.

Если система координат – декартова прямоугольная, то главный вектор перпендикулярен к данной плоскости.

Условие для вектора является необходимым и достаточным условием того, что вектор , заданный относительно общей декартовой системы координат, направлен в положительное полупространство от плоскости, заданной уравнением

относительно той же системы координат.