§ 86. Расстояние от точки до плоскости
Теорема 4. Расстояние d от точки до плоскости, заданной относительно декартовой прямоугольной системы координат общим уравнением
,
вычисляется по формуле
(1)
Доказательство теоремы ничем не отличается от доказательства теоремы § 63.
§ 76. Взаимное расположение двух плоскостей
Пусть относительно общей декартовой системы координат две плоскости заданы своими общими уравнениями
(1)
(2)
Тогда имеют место следующие утверждения.
Для того чтобы плоскости заданные общими уравнениями и в общей декартовой системе координат, пересекались, необходимо и достаточно, чтобы соответствующие коэффициенты при х, у, z в уравнениях и не были пропорциональны.
Для того, чтобы плоскости заданные общими уравнениями и в общей декартовой системе координат, были параллельны, необходимо и достаточно, чтобы соответствующие коэффициенты при х, у, z в уравнениях и были пропорциональны, но чтобы свободные члены не были им пропорциональны, т.е. чтобы существовало такое число
,
что
.
Для того, чтобы плоскости заданные общими уравнениями и в общей декартовой системе координат, совпадали, необходимо и достаточно, чтобы коэффициенты уравнений и были пропорциональны, т.е. существовало такое число
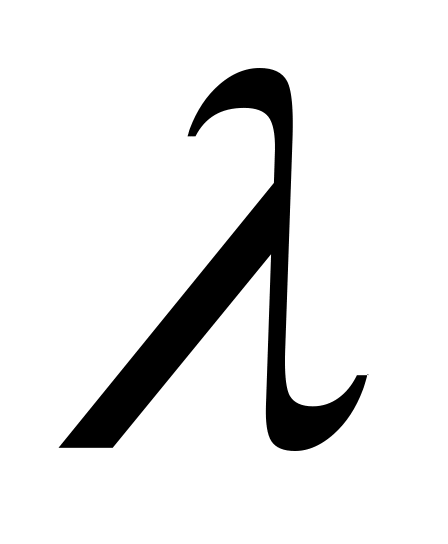что:
,
или
.
(3)
Докажем сначала достаточность признаков.
1. Если
тройки
и
непропорциональны, то найдутся пары
соответствующих чисел из этих троек,
например
и
,
которые также непропорциональны.
Полагая
в данных уравнениях
и
,
получим уравнения
;
определяющие в плоскости хОу уравнения прямых, по которым плоскости и пересекают плоскость хОу (эти прямые есть следы плоскостей и на координатной плоскости хОу). В силу того, что пары и непропорциональны, эти следы пересекаются, следовательно пересекаются и данные плоскости.
2. Если
,
то уравнение
эквивалентно следующему
;
или
.
Свободные члены
и
уравнений
и
в силу условия
различные, значит, любое решение уравнения
не
является решением уравнения
;
это значит, что ни одна из точек, лежащих
на плоскости, заданной уравнением
,
не лежит на плоскости, заданной уравнением
,
следовательно эти плоскости параллельны.
3. Если
то левые части данных уравнений
и
отличаются числовым множителем, не
равным нулю, а значит, эквивалентны.
Необходимость все признаков доказывается сразу методом от противного.
Замечание. Для того чтобы плоскости, заданные общими уравнениями
;
относительно общей декартовой системы координат пересекались, необходимо и достаточно, чтобы выполнялось любое из следующих условий.
Хотя бы один из определителей
был отличен от нуля.
Главные векторы
и
данных плоскостей были бы неколлинеарны.
Необходимое и достаточное условие параллельности двух плоскостей заключаются в выполнении одного из условий
1.
,
но хотя бы один из определителей
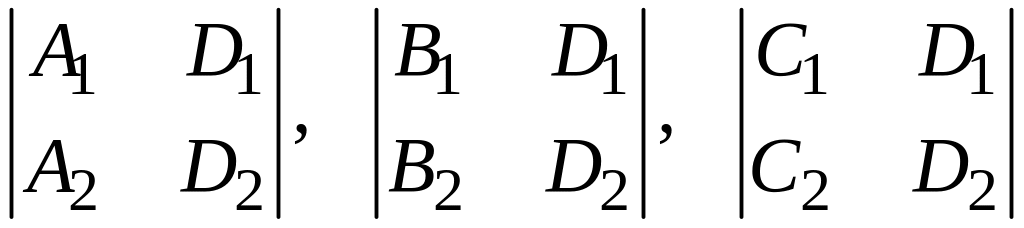
не равен нулю.
2.
Главные векторы
,
данных плоскостей коллинеарны, но
.
3.
Необходимое и достаточное условие совпадения двух плоскостей заключается в выполнении одного из условий
1.
2.
Главные векторы
,
данных плоскостей коллинеарны и
.
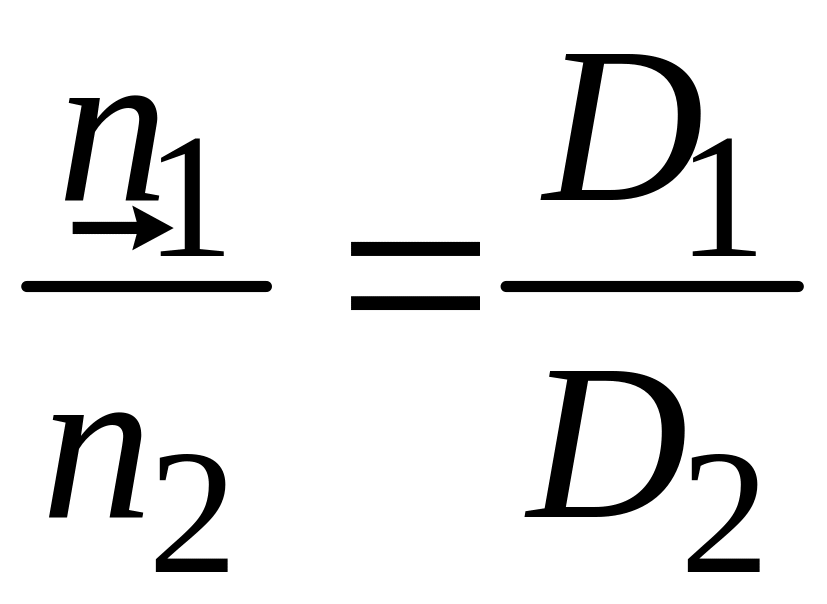3.
Все это лишь другие формулировки уже доказанной теоремы.