
- •3.2.3. Контрольно-измерительные материалы
- •Примерные вопросы и задания для индивидуальной и самостоятельной работы
- •Примерные варианты контрольных работ и тестовых заданий
- •Формы текущего, промежуточного, рубежного и итогового контроля
- •Ранг матрицы.
- •Примерные задачи к коллоквиуму
- •Задачи к экзамену
- •Перечень задач к коллоквиуму
- •Задачи к экзамену
Задачи к экзамену
Найти собственные значения и собственные векторы линейного оператора, заданного матрицей
 .
.Найти собственные значения и собственные векторы линейного оператора, заданного матрицей
 .
.Найти собственные значения и собственные векторы линейного оператора, заданного матрицей
 .
.Привести к диагональному виду матрицы линейного оператора
 .
.Привести к диагональному виду матрицы линейного оператора
 .
.Квадратичную форму
 записать в матричном виде.
записать в матричном виде.Квадратичную форму
 записать в матричном виде.
записать в матричном виде.Дана квадратичная форма
 .
Найти квадратичную форму, полученную
из данной линейным преобразованием
.
Найти квадратичную форму, полученную
из данной линейным преобразованием
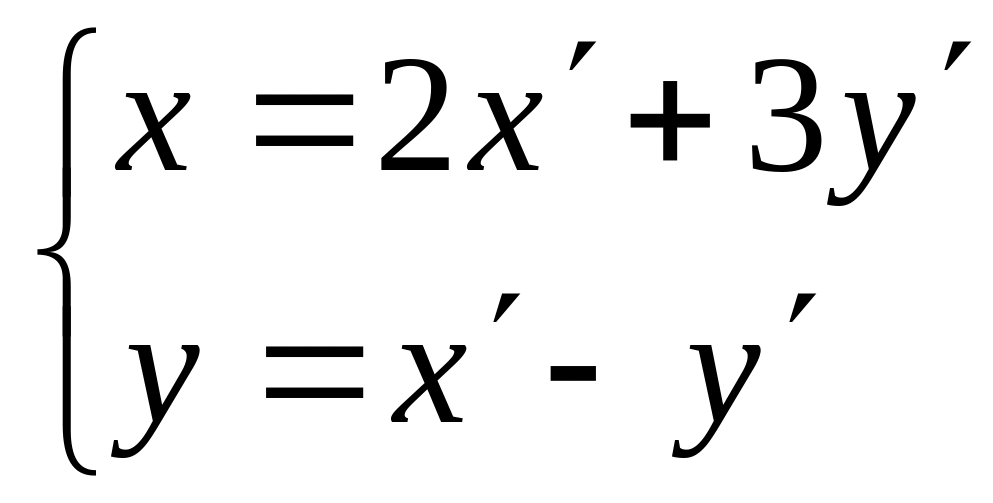 .
.Дана квадратичная форма
 .
Найти квадратичную форму, полученную
из данной линейным преобразованием
.
Найти квадратичную форму, полученную
из данной линейным преобразованием
 .
.Дана квадратичная форма
 .
Найти квадратичную форму, полученную
из данной линейным преобразованием
.
Найти квадратичную форму, полученную
из данной линейным преобразованием
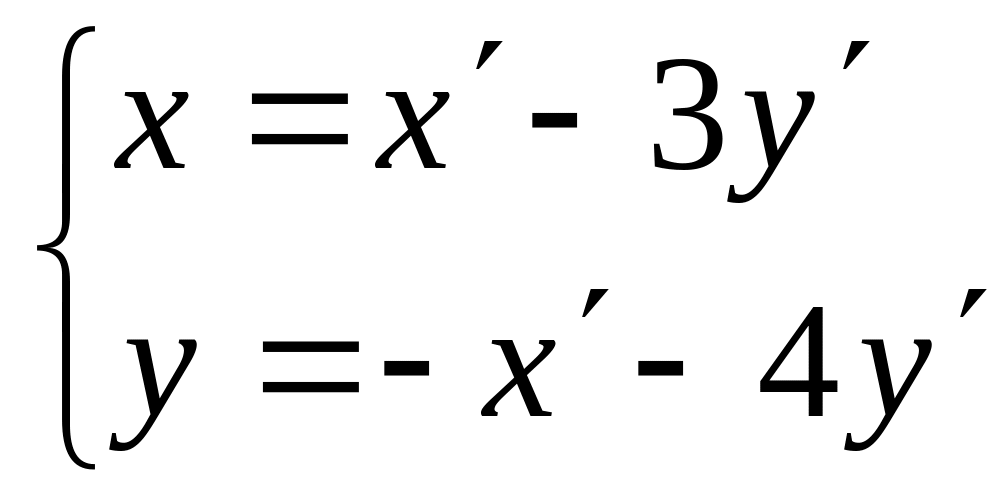 .
.Дан треугольник с вершинами А(-2,0), В(2,4) и С(4,0). Найти Уравнения сторон треугольника, медианы АЕ, высоты АD и длину медианы АЕ.
Найти уравнение множества точек, равноудаленных от оси Оу и точки F(4,0).
Стороны АВ, ВС и АС треугольника АВС заданы соответственно уравнениями 4x+y-5=0, x-3y+10=0, x-2=0. Определить координаты его вершин.
Две стороны параллелограмма заданы уравнениями y=x-2 и x-5y+6=0. Диагонали его пересекаются в начале координат. Найти уравнения двух других сторон параллелограмма и его диагоналей.
Составить уравнение прямой, проходящей через центры окружностей x2+y2=5 и x2+y2+2x+4y-31=0. Найти отношение радиусов окружностей.
Эллипс проходит через точки M1(4,4/5) и M2(0,6). Найти полуоси; координаты фокусов и эксцентриситет эллипса.
Для гиперболы 3x2-4y2=12 найти действительную и мнимую полуоси; координаты фокусов; эксцентриситет; уравнение асимптот.
Составить уравнение параболы, проходящей через точки (0,0) и (-1,-3) симметрично относительно оси Ох.
Составить уравнение параболы, проходящей через точки (0,0) и (2,-4) симметрично относительно оси Оу.
Найти расстояние от начала координат до прямой, проходящей через центр гиперболы
 ,
и вершину параболы
,
и вершину параболы
 .
.
Перечень задач к коллоквиуму
Найти указанные пределы (не используя правило Лопиталя):
 .
.Найти указанные пределы (не используя правило Лопиталя):
 .
.Найти указанные пределы (не используя правило Лопиталя):
 .
.Найти указанные пределы (не используя правило Лопиталя):
 .
.Найти указанные пределы (не используя правило Лопиталя):
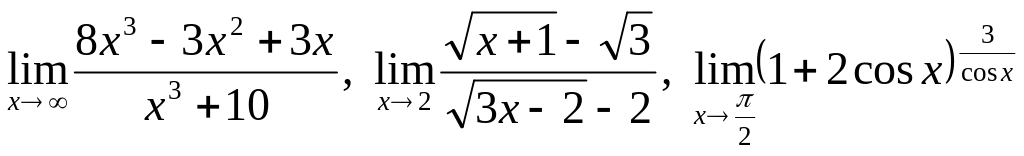 .
.Найти указанные пределы (не используя правило Лопиталя):
 .
.Найти указанные пределы (не используя правило Лопиталя):
 .
.Найти указанные пределы (не используя правило Лопиталя):
 .
.Найти указанные пределы (не используя правило Лопиталя):
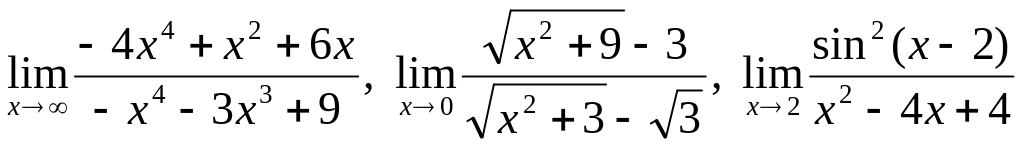 .
.Найти указанные пределы (не используя правило Лопиталя):
 .
.Дана функция
 .
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.
.
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.Дана функция
 .
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.
.
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.Дана функция
 .
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.
.
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.Дана функция
 .
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.
.
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.Дана функция
 .
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.
.
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.Дана функция
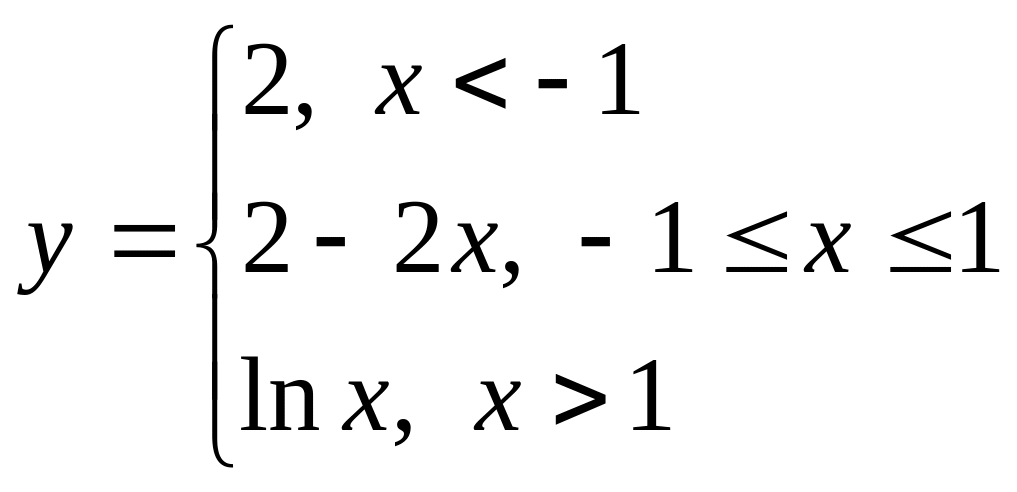 .
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.
.
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.Дана функция
 .
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.
.
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.Дана функция
 .
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.
.
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.Дана функция
 .
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.
.
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.Дана функция
 .
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.
.
Является ли функция непрерывной? В
случае нарушения непрерывности
установить характер точек разрыва.Найти производные
 .
.Найти производные
 .
.Найти производные
 .
.Найти производные
 .
.Найти производные
 .
.Найти производные
 .
.Найти производные
 .
.Найти производные
 .
.Найти производные
 .
.Найти производные
 .
.Найти производную функции, заданной неявно:
 .
Найти
.
Найти
 и
и
 для функции, заданной параметрически:
для функции, заданной параметрически:
 .
.Найти производную функции, заданной неявно:
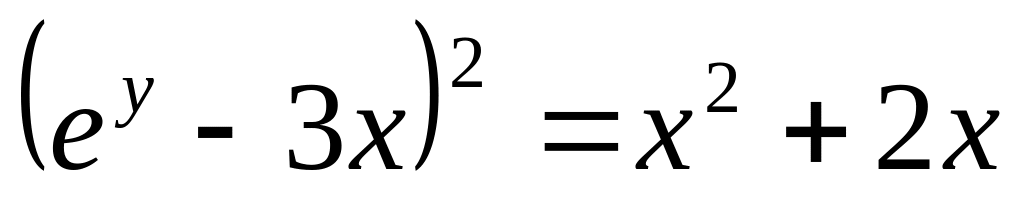 .
Найти
и
для функции, заданной параметрически:
.
Найти
и
для функции, заданной параметрически:
 .
.Найти производную функции, заданной неявно:
 .
Найти
и
для функции, заданной параметрически:
.
Найти
и
для функции, заданной параметрически:
 .
.Найти производную функции, заданной неявно:
 .
Найти
и
для функции, заданной параметрически:
.
Найти
и
для функции, заданной параметрически:
 .
.Найти производную функции, заданной неявно:
 .
Найти
и
для функции, заданной параметрически:
.
Найти
и
для функции, заданной параметрически:
 .
.Найти производную функции, заданной неявно:
 .
Найти
и
для функции, заданной параметрически:
.
Найти
и
для функции, заданной параметрически:
 .
.Найти производную функции, заданной неявно:
 .
Найти
и
для функции, заданной параметрически:
.
Найти
и
для функции, заданной параметрически:
 .
.Найти производную функции, заданной неявно:
 .
Найти
и
для функции, заданной параметрически:
.
Найти
и
для функции, заданной параметрически:
 .
.Найти производную функции, заданной неявно:
 .
Найти
и
для функции, заданной параметрически:
.
Найти
и
для функции, заданной параметрически:
 .
.Найти производную функции, заданной неявно:
 .
Найти
и
для функции, заданной параметрически:
.
Найти
и
для функции, заданной параметрически:
 .
.
