Примерные варианты контрольных работ и тестовых заданий

Итоговый тест ЛА и АГ

1. При каких значениях а, b, с для матрицы.

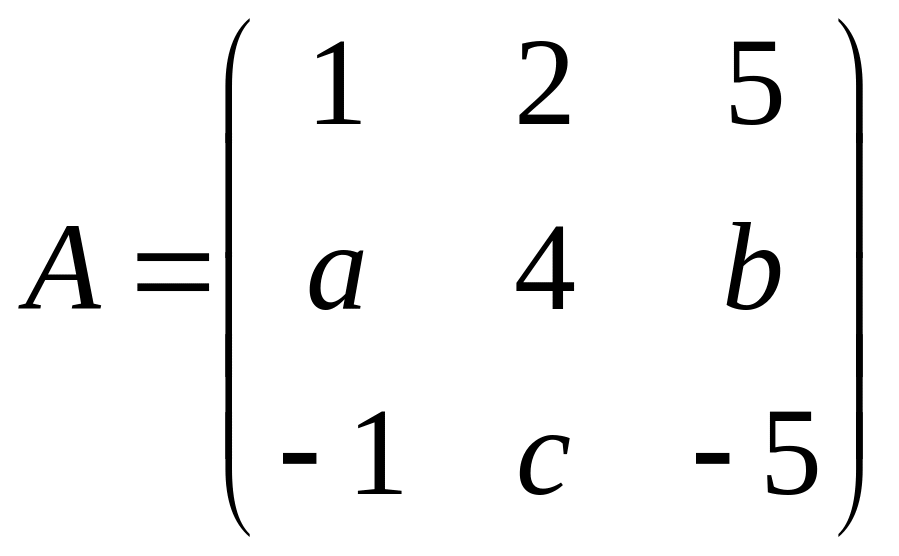
выполняется равенство А2 = 0 ?

2. Дана матрица

.

Найти определитель матрицы В = АА'.

3. Выяснить, какие из приведенных ниже матриц являются нулевыми (А и В — квадратные матрицы):

1) ВА – АВ

2) (В'А)' — А'В;

3) А-1 В-1 – В-1А-1;

4) (А-1В)-1 –АВ-1;

5)АА' — А'А.

4. Даны матрицы:

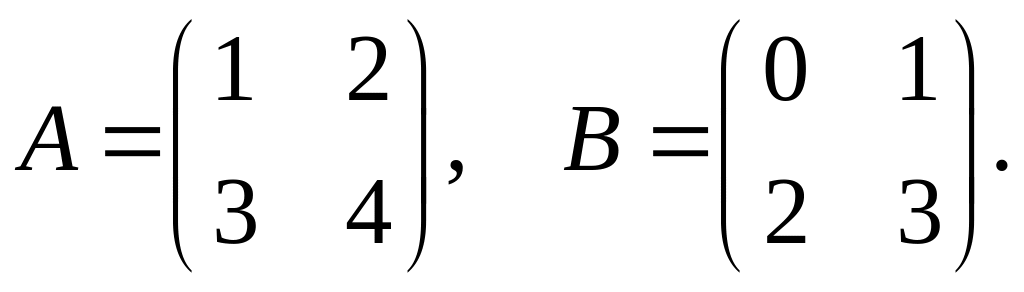
Найти след tr С матрицы С = АВ - ВА + А + В.

5. Выяснить, при каком значении а ранг матрицы А является наименьшим среди рангов приведенных матриц:

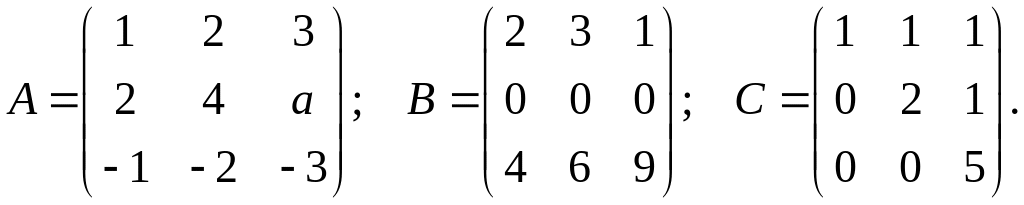
6. По формулам Крамера решить систему уравнений:

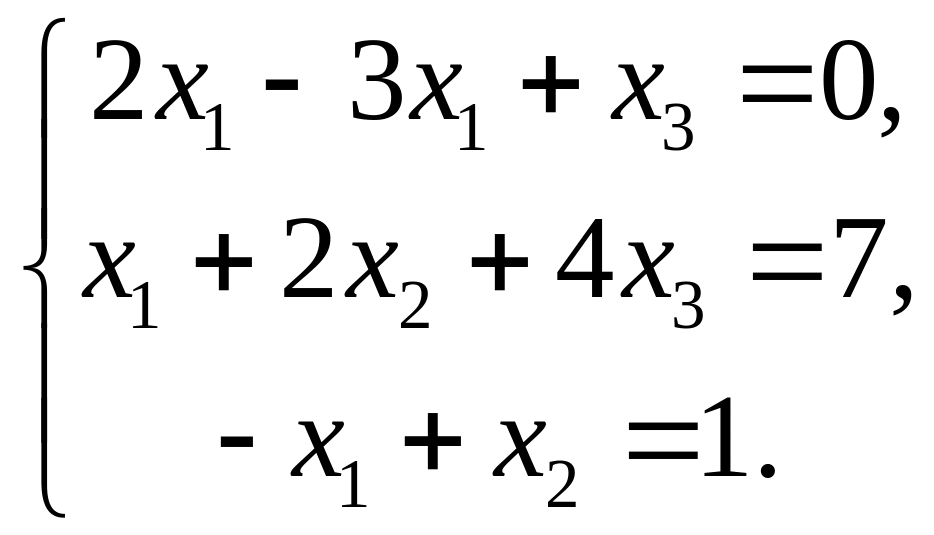
В ответе дать значения переменных х1, х2 и определителя .

7. Выяснить, какой из методов можно применить для решения системы уравнений:

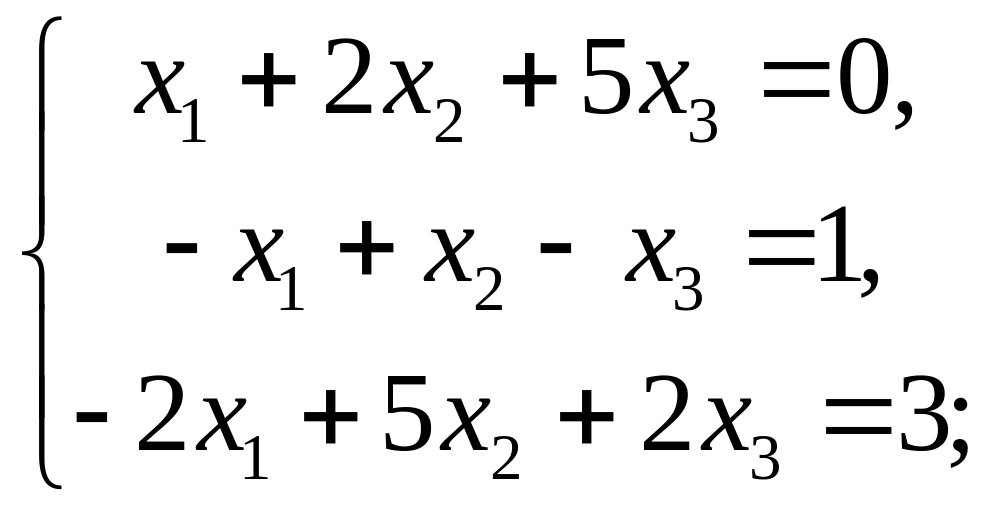
1) метод обратной матрицы; 2) по формулам Крамера; 3) метод Гаусса.

8. Дано матричное уравнение АХВ = С. Его решение с помощью обратных матриц А-1, В-1 имеет вид:

1. A-1B-1C;

2. B-1CA-1;

3. A-1CB-1;

4. CA-1B-1.

9. Для системы уравнений

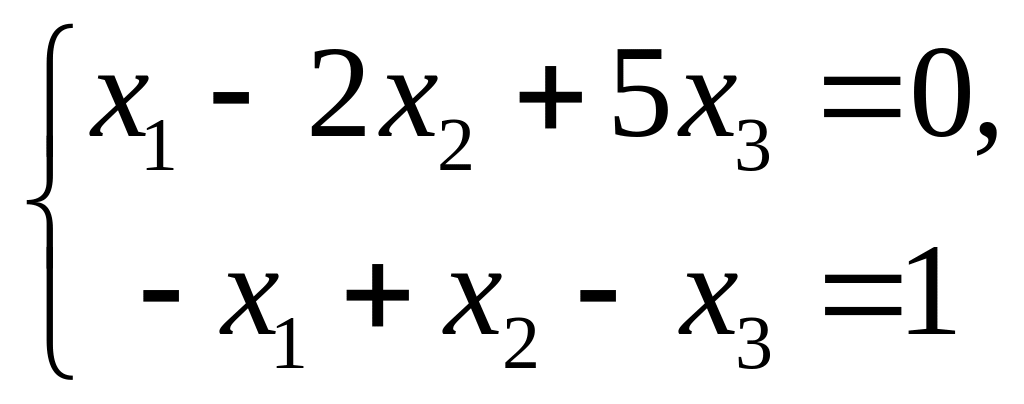
найти базисное решение (x1,x2,x3), получаемое при выборе в качестве основных (базисных) переменных x1,x2.

10. Для системы уравнений

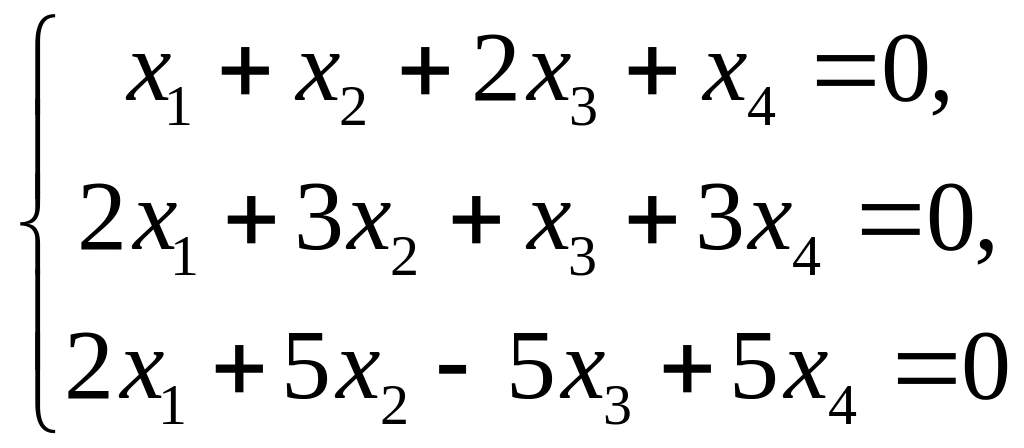
найти фундаментальную систему решений. В ответе дать число таких решений.

11. Дана матрица прямых затрат А в модели Леонтьева:

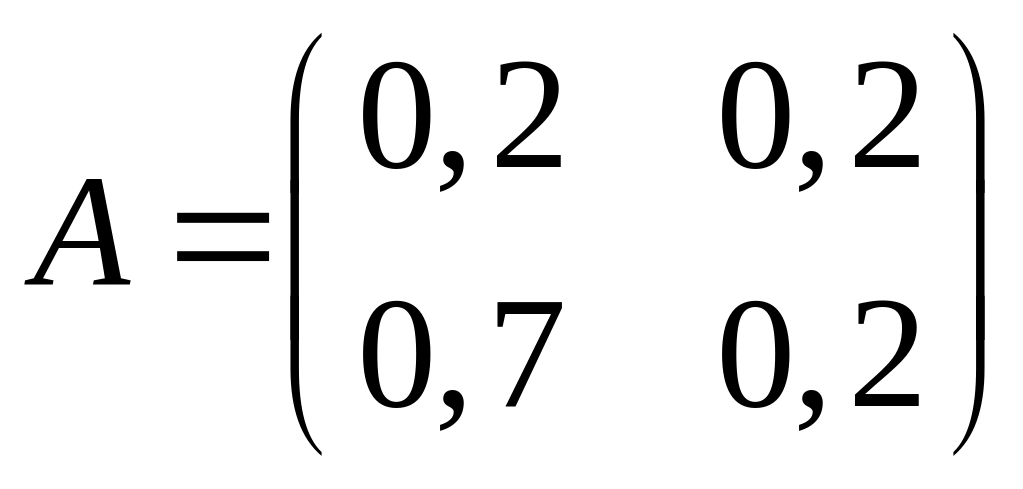. Найти матрицу полных затрат S. В ответе дать ее элементы s11 и s21.

12. Две стороны квадрата лежат на параллельных прямых Зх + 4у +25 = 0 и Зх + 4у + 50 = 0. Найти площадь квадрата.

13. В треугольнике ABC заданы вершины А(0; 2), В(4; 0) и точка пересечения высот . Найти уравнение стороны ВС.

Ответ: 4х + By + С = 0, где В = ... , С = ... .

14. Составить уравнение биссектрисы тупого угла между прямыми Зх+у-12 = 0 и y = 0.

Ответ: Зх + By + С = 0, где В = ... ,С = ... .

15. Траектория движения линии, расстояние каждой точки которой от точки А(2; -2) вдвое меньше, чем от прямой х + 1 = 0, есть:

1) прямая линия; 2) окружность; 3) эллипс; 4) гипербола; 5) парабола.

16. Составить уравнение прямой, проходящей через центр гиперболы и вершину параболы у = -2х2 + 16х - 30.

Ответ: х + By + С = 0, где В = ... , С= ... .

17. Составить уравнение плоскости, проходящей через точку (-1; 2; -3) и перпендикулярно прямой

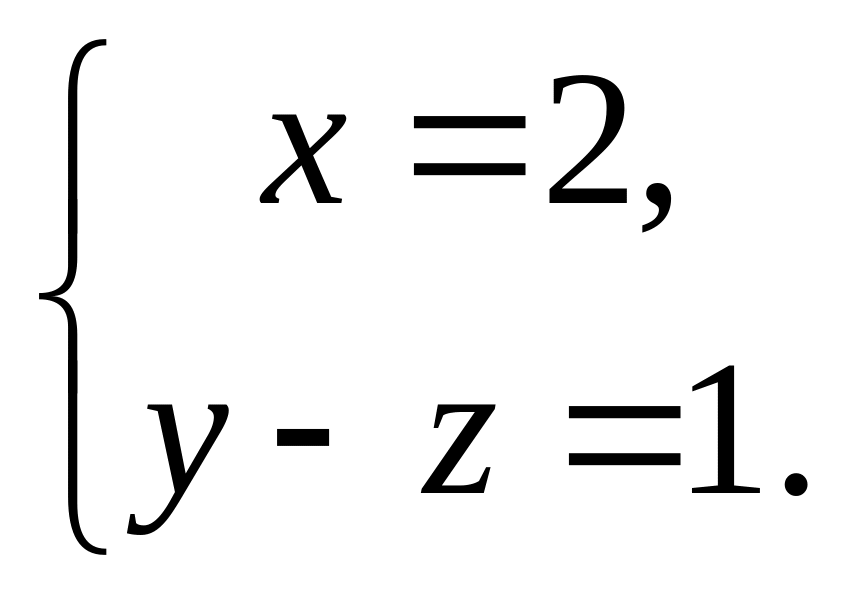
Ответ: Зх + Ву + С=0, где В= ... ,С= ... .

18. Найти (в градусах) угол между плоскостью y=z и прямой

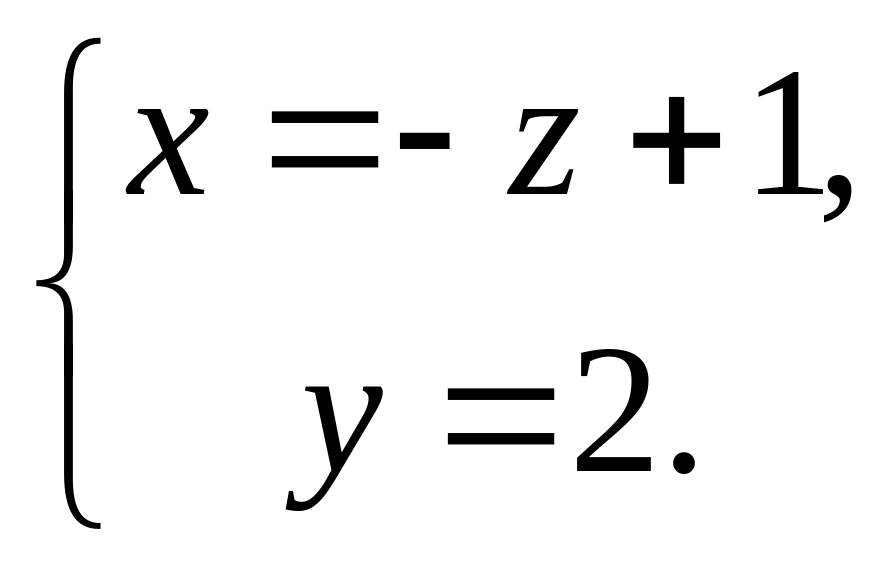
19. Найти (в градусах) угол между векторами — единичные векторы, образующие угол 120°.

20. Найти (с точностью до 0,1) проекцию вектора а = (2; -3; 4) на ось, составляющую с координатными осями равные острые углы.

21. Выяснить, при каком значении векторы а1=(-2; 0; 1); а2=(1; -1; 0); а3=(0; 1; ) не образуют базис в пространстве R3.

22. Выяснить, при каком значении вектор b=(1; ,) линейно выражается через векторы а1=(2;1) и а2=(4;2).

23. Векторы х1 = (—1; а) и х2 = (b; 1) являются собственными векторами матрицы 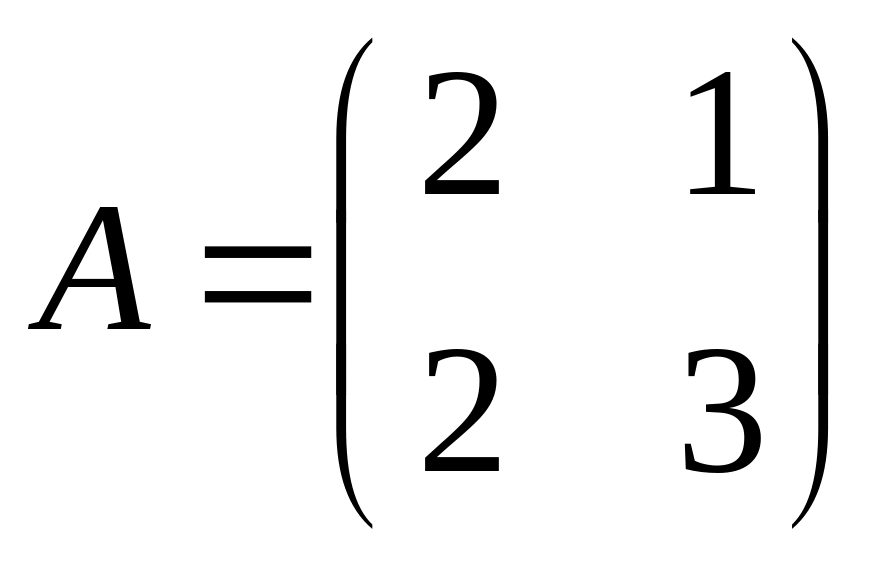с собственными значениями 1, 2( 1< 2) соответственно. Найти 1, 2 и значения а и b.

24. Найти наименьшее целое значение ,, при котором будет положительно определенной квадратичная форма

Тест 2

1. Правило Лопиталя не может быть применено для нахождения предела:

1. :Найти предел

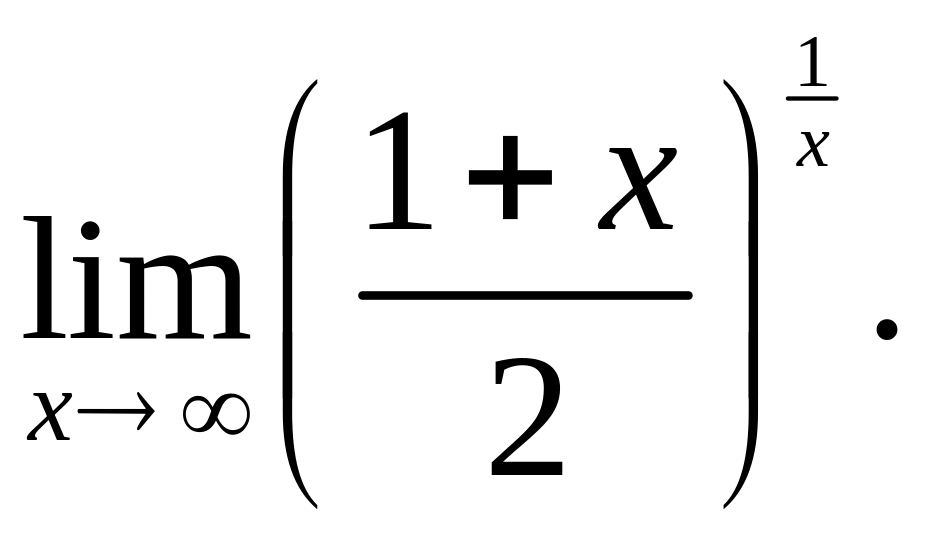
2. Выяснить, к какой из приведенных ниже функций не может быть применена теорема Лагранжа на отрезке [0; 2]:

4. Среди перечисленных функций убывает на всей области определения функция:

4. Найти длину интервала возрастания функции у = Зх – х3.

5. Выяснить, какое из приведенных утверждений является неверным:

1. в точке экстремума производная функции равна нулю или не существует;

2. в точке экстремума функция меняет знак;

3. в точке экстремума производная меняет знак;

4. в точке, в которой производная равна нулю или не существует, может не быть экстремума?

7. Найти точку x0 максимума функции у = х2 (х - 4)2.

8. Среди перечисленных функций горизонтальную асимптоту имеет функция:

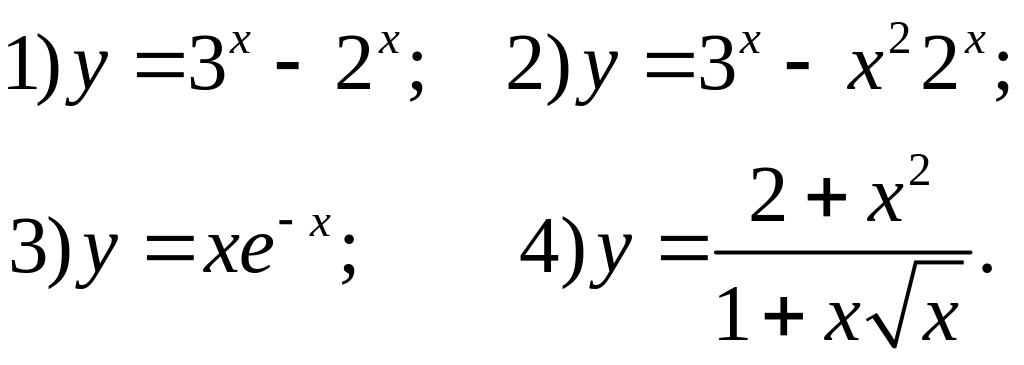
7. Следующее утверждение из перечисленных является всегда верным:

1. в точке перегиба всегда существует конечная 1-я производная;

2. в точке перегиба существует конечная 2-я производная;

3. точка перегиба является точкой экстремума 1-й производной функции;

4. точка перегиба является точкой экстремума 2-й производной функции

10. Найти наибольшее и наименьшее значения функции у = х3 + х2 на отрезке [-1; 2].

11. Требуется огородить прямоугольную площадку площадью 600 кв. м и перегородить ее таким же забором пополам. При каких размерах а, b площадки расход материала на забор будет наименьшим?

12. Если изобразить на одном рисунке графики предельных и средах издержек, то:

1. они будут пересекаться в точке минимума средних издержек;

2. они будут пересекаться в точке минимума предельных издержек;

1. они будут пересекаться в точке, в которой предельные издержки равны нулю;

2. график средних издержек будет в любом случае выше графика предельных издержек.

13. . Функция издержек имеет вид

При какой цене р за единицу товара оптимальное значение выпуска xопт=30?

Тест 3

1. При каких а и b функция является первообразной для f(x) = (2х +1)2 ?

2. При каких целых а, b, с функция F(x) = 2e3x+1 является первообразной для функции f{x) = аеbx+c ?

3. При каких целых а, b, с функции являются первообразными для одной и той же функции f(x)?

4. Найти

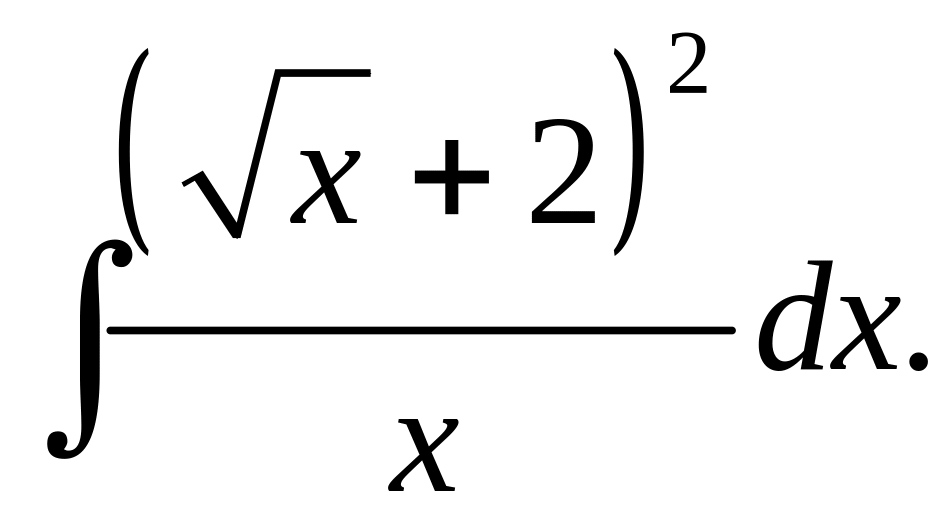
Ответ: , где a, b, d — целые числа: а = ... , b = ..., d = .... .

5. Найти

Ответ: 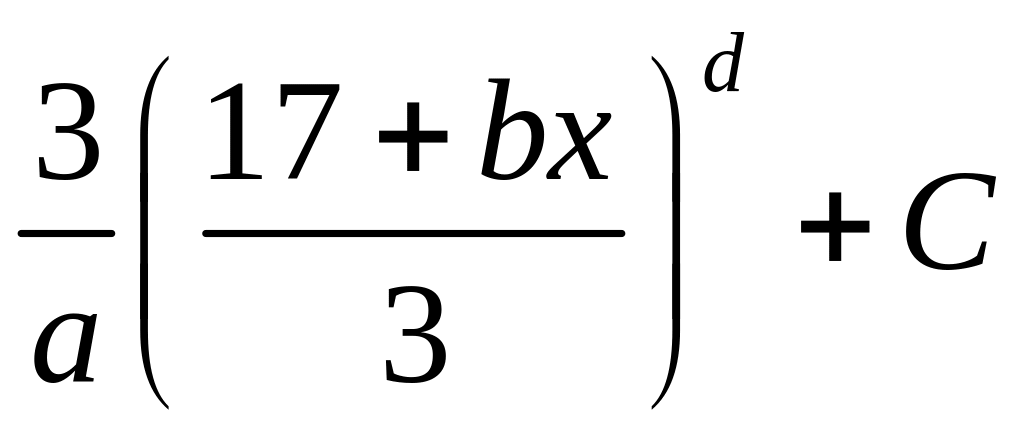, где a, b, d — целые числа: а = ... , b = ..., d = .... .

6. Найти

Ответ: , где a,b,d — целые числа, дробь - несократима, b>0: a = ..., b=..., d=.... .

7. Найти

Ответ: , где a, b, d— целые числа, дробь a / b — несократима, b а>0: а= ... , b = ... , d= ... .

8. Найти

Ответ: , где a, b, d — целые числа: а = ... , b = ... , d= ... .

9. Найти

Ответ: 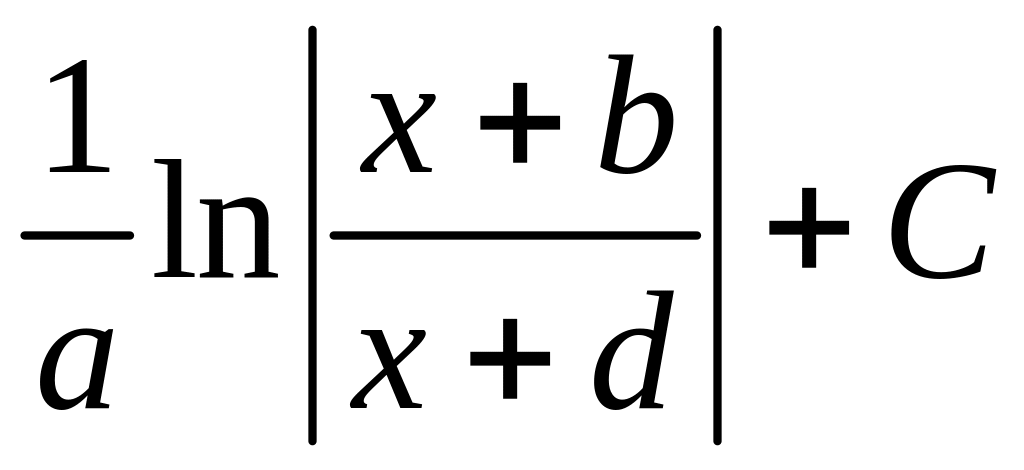, где a, b, d — целые числа, а > 0: а = ... , b = ... , d= ... .

10. Найти

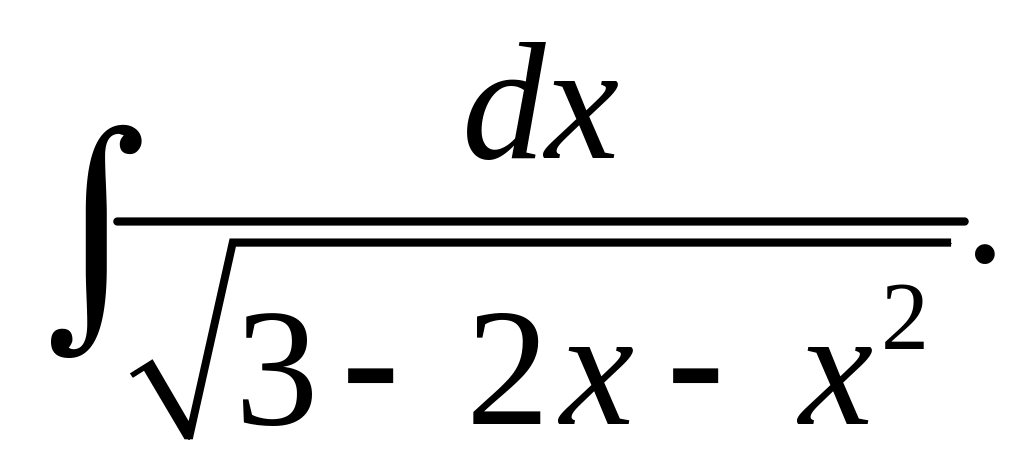
Ответ: , где a, b, d — целые числа, а > 0: а = ... , b = ... , d= ... .