Б) Операції над лінійними перетвореннями

Сумою двох лінійних перетворень А та ℬ називається таке перетворення А+В, при якому

Властивості:

1. А+В = В+А.

2. (А+В)+С = А+(В+С).

3. А+ Ơ = А.

Добутком лінійного перетворення А на число α називається таке теж лінійне перетворення αА, при якому

Властивості:

1. 1·А = А.

2. α(βА)=(αβ)А.

3. (α+β)А=αА+βА.

4. α(А+В)=αА+αВ.

Добутком лінійних перетворень А та В називається таке теж лінійне перетворення АВ, при якому

Властивості:

1. (АВ)ℂ=А(Вℂ).

2. Аℰ=А.

3. (А+В)ℂ=Аℂ+Вℂ.

4. ℂ(А+В)=ℂА+ℂВ.

Для кожного невиродженого лінійного перетворення А існує таке (обернене до А) лінійне перетворення А^-1, що

А∙А^-1=А^-1·А=ℰ.

Ясно, що добуток невироджених лінійних перетворень теж є невиродженим лінійним перетворенням.

В) Перехід до нового базису

Нехай лінійне перетворення А в базисі е=(е₁,е₂,…,е_п) має матрицю А, а в базисі - матрицю . Знайдемо зв’язок між ними.

Позначимо через С матрицю переходу від базису е до базису . Тоді

Будемо матрицю переходу С розглядати як матрицю лінійного перетворення С в базисі е. Тоді

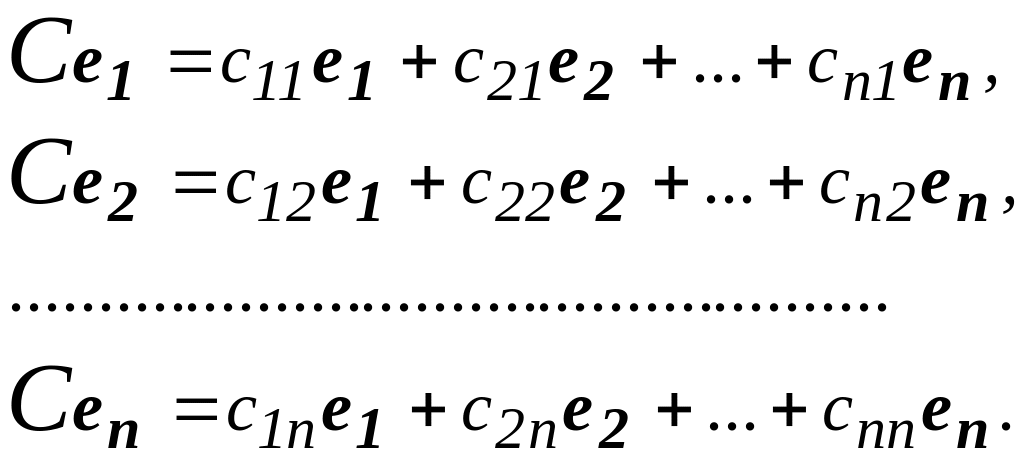
Значить, лінійне перетворення С переводить вектори базису е у вектори базису . Відомо, що тоді визначник матриці С відмінний від нуля, значить, для С існує обернене перетворення С^-1, при якому

За умовою,

.

Застосуємо до обох частин цієї рівності перетворення С^-1:

.

Підставимо в ліву частину :

,

тобто матрицею перетворення в базисі е є матриця Але, з другого боку матриця цього перетворення рівна добутку матриць відповідних перетворень в базисі е, тобто .

Ясно, що визначник матриці лінійного перетворення не залежить від базису:

Приклад.

В базисі е₁, е₂ перетворення А має матрицю

Написати матрицю цього перетворення в базисі

Розв’язування.

Матриця переходу Тоді Звідси

Г) Ранг і дефект лінійного перетворення

Сукупність всеможливих векторів вигляду Ах, де , називається областю значень або образом лінійного перетворення А. Позначається ImА.

Сукупність всеможливих векторів , для яких Ах=0, називається ядром лінійного перетворення А. Позначається KerА.

І образ, і ядро лінійного перетворення А є підпростором в V.

а) Якщо ImА, то х=Ах₁, у=Ау₁, де ,

то х+у=Ах₁+Ау₁=А(х₁+у₁), де і, значить, ImА ,

αх=αАх₁=А(αх₁), де і, значить, αх ImА .

Отже, ImА – підпростір простору V.

б) Якщо KerА, тобто якщо Ах=0 і Ау=0, то і

А(х+у)= Ах+Ау=0+0=0 і А(αх)=αАх=α·0=0,

тобто KerА і KerА.

Отже, KerА – підпростір простору V.

Розмірність образу перетворення А dim(ImА) співпадає з рангом матриці А цього перетворення і називається рангом перетворення А. Дійсно, підпростір ImА породжується векторами Ае₁, Ае₂,..., Ае_п, де е={e₁, e₂,…, e_n} – довільний базис простору V і, значить, розмірність ImА дорівнює максимальній кількості лінійно незалежних стовпчиків матриці А.

Розмірність ядра dim(KerА) називається дефектом лінійного перетворення А.

Важливим є твердження, що сума рангу і дефекту лінійного перетворення А дорівнює розмірності п простору V. Тобто,

dim(ImА) + dim(KerА) = n.