
- •Векторні простори
- •§1. Основні поняття а) Означення
- •Б) Розмірність і базис
- •§2. Лінійні перетворення а) Основні поняття
- •Б) Операції над лінійними перетвореннями
- •В) Перехід до нового базису
- •Г) Ранг і дефект лінійного перетворення
- •Д) Інваріантні підпростори
- •Е) Власні вектори і власні значення лінійного перетворення
- •Звідси із лінійної незалежності векторів e1,e2,…,en випливає:
Лекція 8
Векторні простори
§1. Основні поняття а) Означення
Множина V елементів x, y, z,… називається лінійним, або векторним, простором, якщо сума х+у довільних двох її елементів х, у і добуток αх кожного її елемента х на будь-яке число α теж належать множині V, причому виконуються наступні умови:

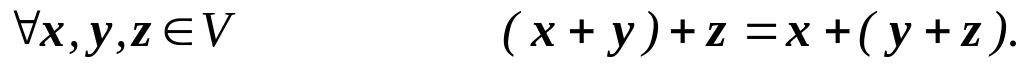
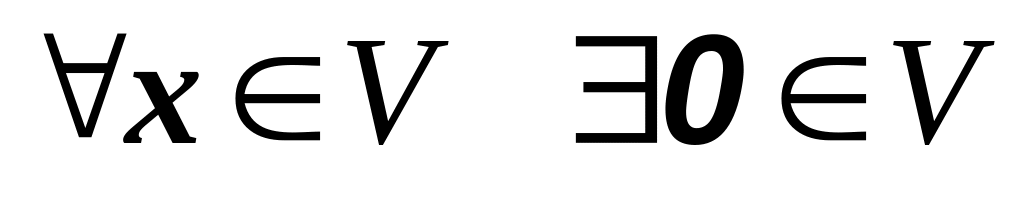
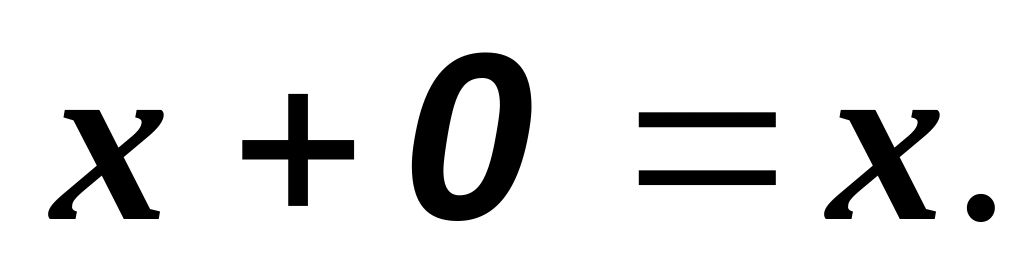 0
–
називають нульовим елементом.
0
–
називають нульовим елементом.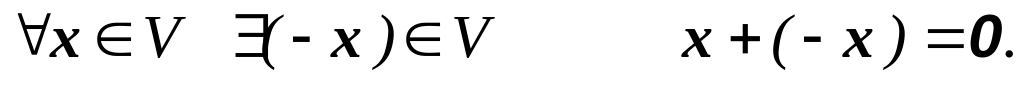 –х
називають елементом, протилежним до
х.
–х
називають елементом, протилежним до
х.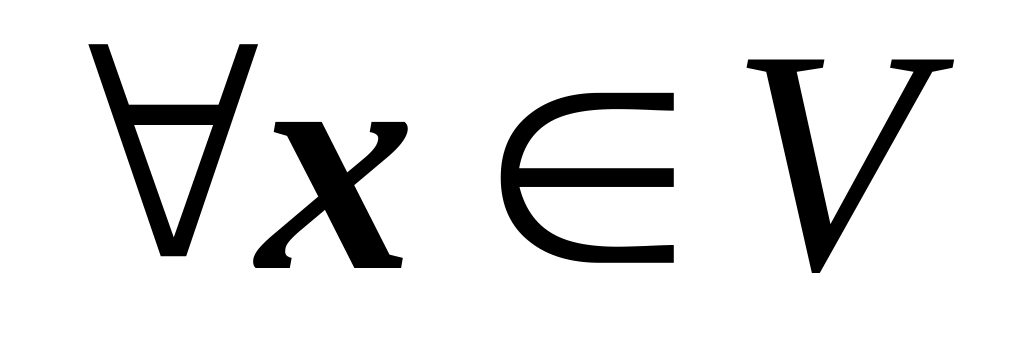 1·х=х.
1·х=х.


Елементи векторного простору називають векторами.
Приклади векторних просторів.
Множина многочленів не вище п-го степеня з дійсними коефіцієнтами.
Множина розв’язків системи лінійних однорідних рівнянь.
Множина всеможливих рядків, які містять п дійсних чисел.
Якщо в просторі V визначено множення його елементів на дійсні (комплексні) числа, то V називають дійсним (комплексним) векторним простором.
Із означення векторного простору випливають наступні властивості.
Єдиність нуля.
Якщо припустити існування двох нульових елементів 01 і 02, то із 01+02=01 та 02+01=02 і того, що 01+02=02+01, випливає 01=02.
Єдиність протилежного елемента.
Якщо припустити існування двох протилежних до х елементів y та z, таких, що х+у=0 і х+z=0, то із
y+x+z=y+(x+z)=y+0=y та
y+x+z=(y+x)+z=0+z=z
випливає y=z.
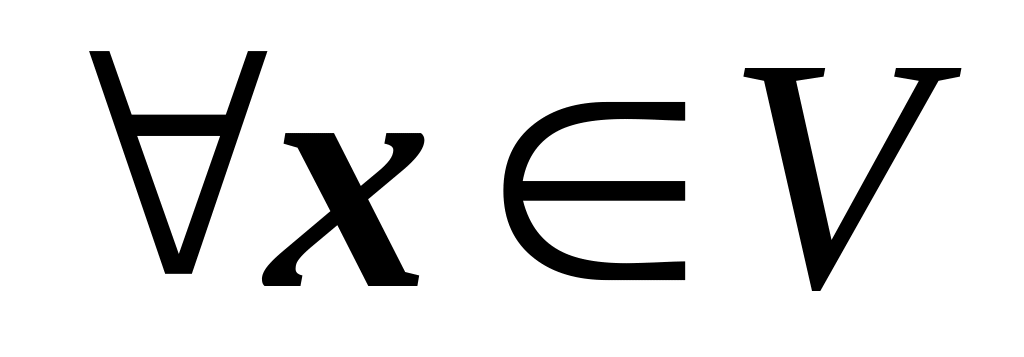 0
·
x
=
0.
0
·
x
=
0.
Дійсно, 0 · x = (0 + 0) x = 0 · x + 0 · x. Додавши до обох частин рівності - 0 · x , отримаємо 0 = 0 · x.
Дійсно,
![]() Додавши до обох частин рівності
Додавши до обох частин рівності
![]() отримаємо
отримаємо
![]()
Якщо добуток αх=0, то або α=0, або х=0.
Дійсно,
якщо
![]() то
то
![]()
 є
протилежним до х.
є
протилежним до х.
Дійсно, х+(-1)х=1·х+(-1)х=[1+(-1)]x=0·x=0, звідки (-1)х= -х.
Б) Розмірність і базис
Вектори
а1,
а2,…,аk
векторного простору V
називаються лінійно
залежними,
якщо існують такі числа
![]() одночасно не рівні нулю, що
одночасно не рівні нулю, що
![]()
В іншому випадку вектори називають лінійно незалежними.
Якщо
вектори а1,а2,…,аk
лінійно залежні, тобто
![]() ,
і, наприклад,
,
і, наприклад,
![]() то
то
![]()
тобто
![]() де
де
![]()
Це означає, що вектор аk є лінійною комбінацією решти векторів системи. Отже, якщо вектори а1, а2,…,аk лінійно залежні, то, принаймні, один із них лінійно виражається через решту. Ясно, що справедливе і зворотнє твердження.
Максимальна кількість лінійно незалежних векторів системи векторів а1, а2,…,аk називається рангом цієї системи. Позначають rank{ а1, а2,…,аk}.
Довільна
матриця
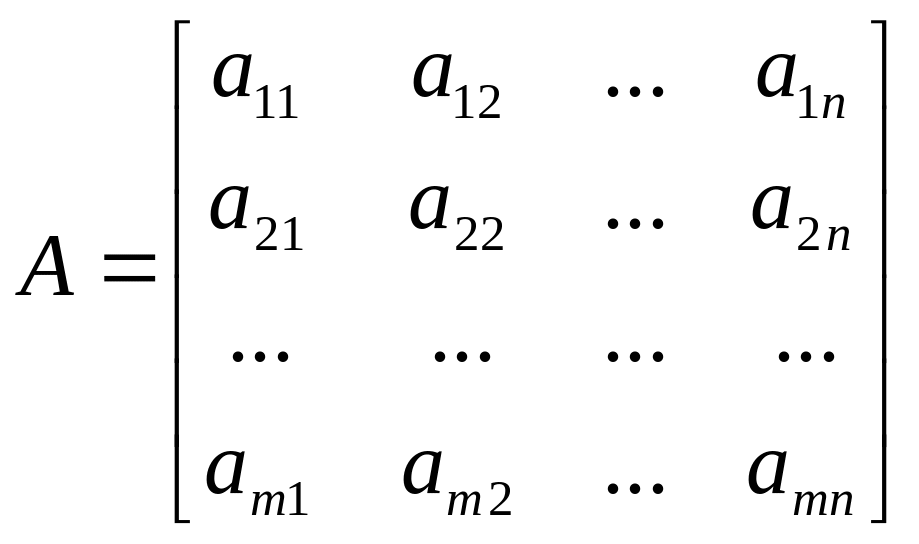 містить дві системи векторів:
містить дві системи векторів:
систему векторів – рядків {а1,а2,…,аm} і систему векторів – стовпчиків
![]() ,
де аі=(аі1,аі2,…,аіп),
і=1,2,…,m,
,
де аі=(аі1,аі2,…,аіп),
і=1,2,…,m,
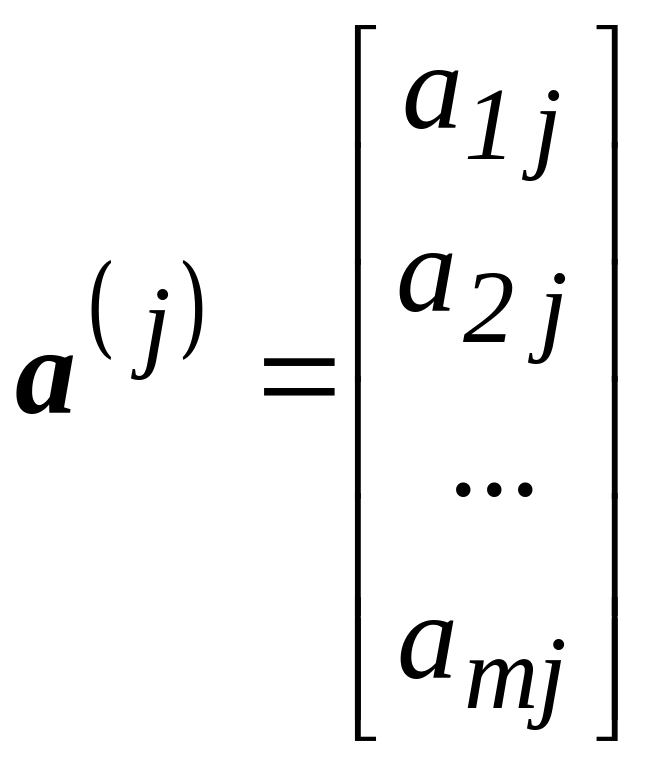 ,
j=1,2,…,n.
,
j=1,2,…,n.
Ранг системи рядків довільної матриці А дорівнює рангу її стовпчиків і називається рангом матриці А. Позначається rankA або r(A).
Таким чином, для знаходження рангу матриці досить з допомогою елементарних перетворень над рядками (стовпчиками) звести її до ступінчастого вигляду і підрахувати кількість ненульових рядків (стовпчиків), яка й дорівнюватиме кількості лінійно незалежних серед них, а, отже, рангу матриці.
Приклад.
Знайти ранг матриці.
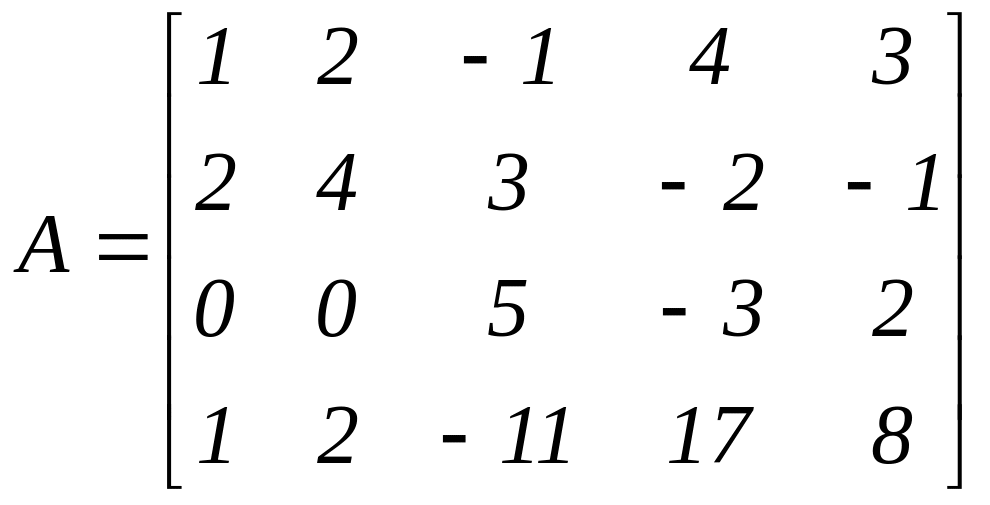 .
.
Розвязання.
Зведемо матрицю А до ступінчастого вигляду з допомогою елементарних перетворень її рядків:

Отже, r(A)=3.
Розмірністю векторного простору V називається максимальна кількість лінійно незалежних векторів, що містяться в ньому. Позначається dimV
(від dimage-фр).
Наприклад, розмірність множини всіх векторів площини дорівнює два, розмірність множини просторових векторів – три. Простори із скінченною розмірністю називаються скінченновимірними.
Базисом простору V називають впорядковану скінченну систему векторів, якщо:
вона лінійно незалежна;
кожний вектор простору V є лінійною комбінацією векторів цієї системи.
Коефіцієнти даної лінійної комбінації називаються компонентами або координатами вектора за цим базисом.
В заданому базисі компоненти вектора визначаються однозначно.
Дійсно,
при двох заданнях вектора х
в базисі а1,а2,…,аk,
зокрема,
![]() та
та
![]() ,
отримаємо
,
отримаємо
![]() Оскільки всі коефіцієнти
Оскільки всі коефіцієнти
![]() (бо система а1,
а2,…,аk
лінійно незалежна), то
(бо система а1,
а2,…,аk
лінійно незалежна), то
![]()
В п-вимірному просторі кожна впорядкована лінійно незалежна система із п лінійно незалежних векторів є базисом. Ясно, що в п-вимірному просторі кожну впорядковану лінійно незалежну систему із k<n векторів можна доповнити до базису.
Розглянемо
в просторі V
два базиси: е=(е1,е2,…,еп)
та
![]() (перший з них назвемо старим, а другий
– новим). Виразимо кожний вектор нового
базису через вектори старого базису:
(перший з них назвемо старим, а другий
– новим). Виразимо кожний вектор нового
базису через вектори старого базису:

Можна сказати, що нові базисні вектори виражаються через старі з допомогою матриці
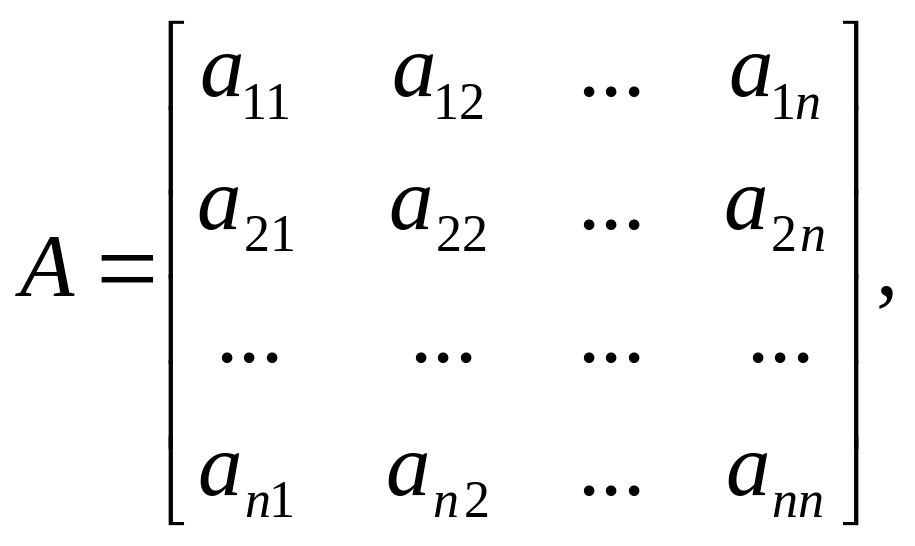
стовпчиками якої
є коефіцієнти їх розкладу за векторами
старого базису. Матриця А називається
матрицею переходу від базису е
до базису
![]() .
Матриця переходу є невиродженою, оскільки
в іншому випадку її стовпчики, а, отже,
і вектори
.
Матриця переходу є невиродженою, оскільки
в іншому випадку її стовпчики, а, отже,
і вектори
![]() ,
були б лінійно залежними.
,
були б лінійно залежними.
Розглянемо зв’язок між координатами одного і того ж вектора в старому і новому базисах.
Нехай
х=х1е1+х2е2+…+хпеп
і
![]()
Підставивiи замість їх вирази через е1,е2,…,еп, отримаємо
![]()
Із єдиності розкладу вектора х за базисом е1,е2,…,еп, випливає
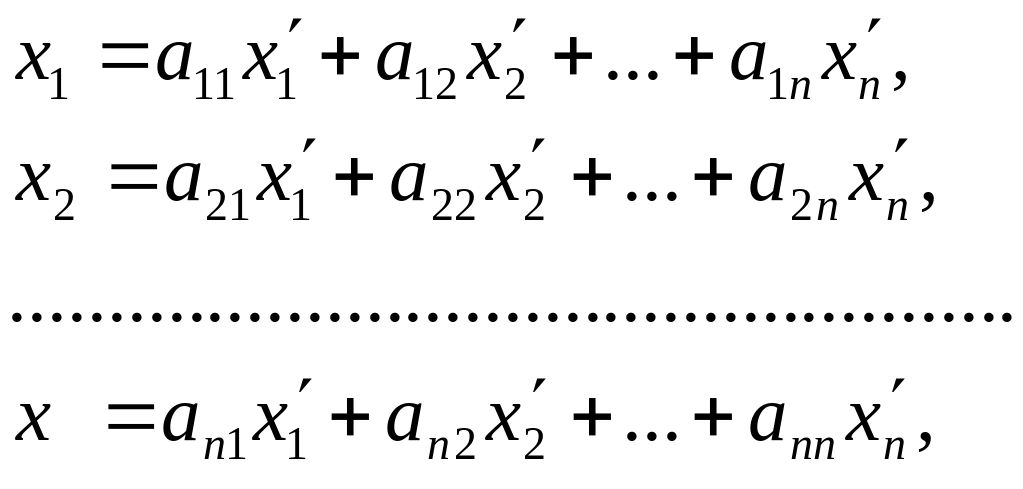 звідки
звідки
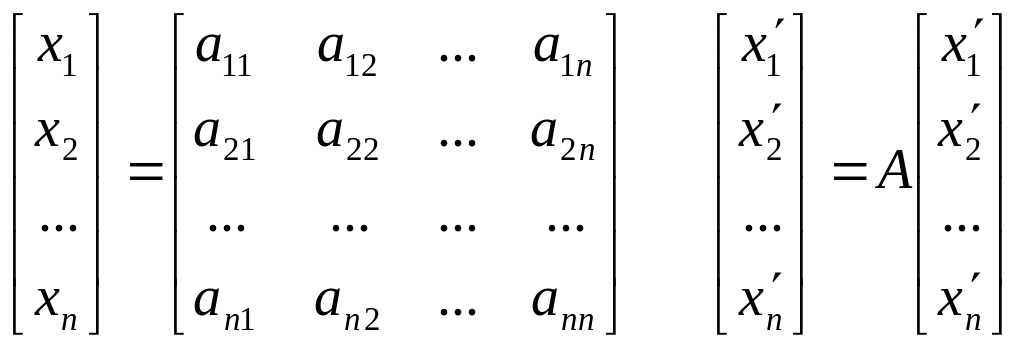 .
.
Таким чином, старі координати вектора отримуються із нових з допомогою тієї ж матриці А, тільки коефіцієнти відповідних розкладів утворюють тепер рядки цієї матриці.
Приклад.
Нехай е1,
е2 – одиничні
вектори, розташовані вздовж осей
прямокутної декартової системи координат.
Повернемо осі координат на кут φ
проти годинникової стрілки і позначимо
нові базисні вектори через
![]() та
та
![]() .
Кути, утворені вектором
з векторами е1 і
е2, рівні відповідно
φ і
.
Кути, утворені вектором
з векторами е1 і
е2, рівні відповідно
φ і
![]()
(див. малюнок). Тому
координати цього вектора в базисі е1,
е2 рівні
![]() і
і
![]() значить,
значить,
![]() .
Аналогічно, кути вектора
.
Аналогічно, кути вектора
![]() з векторами е1
і е2 рівні
відповідно
з векторами е1
і е2 рівні
відповідно
![]() і φ, тому координати його в базисі
і φ, тому координати його в базисі
е1,
е2 рівні
![]() і
,
значить,
і
,
значить,
![]()

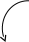
φ
φ
e1
![]() e2
e2![]()
![]()




Таким чином, матриця
переходу від базису е1,
е2 до базису
![]() ,
матиме вигляд
,
матиме вигляд
![]()
Тоді старі координати виражаються через нові так:
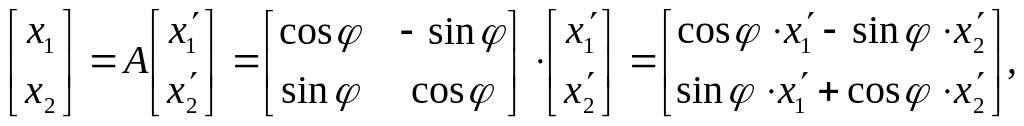
звідки
![]()
в) Підпростори векторного простору
Підпростором векторного простору V називається сукупність V1 його елементів, яка сама є векторним простором відносно введених в V операцій додавання і множення на число.
Для встановлення
того, що деяка підмножина V1
векторного простору V є його
підпростором, досить показати, що для
довільних двох векторів х та у
із V1 їх сума х+у
теж належить V1, і що для
довільного вектора
![]() і довільного
і довільного
![]() добуток
добуток
![]() теж належить V1. Це твердження
випливає із аксіом 1, 2, 5-8 векторного
простору.
теж належить V1. Це твердження
випливає із аксіом 1, 2, 5-8 векторного
простору.
Приклади.
У звичайному тривимірному векторному просторі підпросторами є всі площини і всі прямі, які проходять через початок координат.
Сам простір V і множина із одного нульового елемента теж є підпросторами простору V (тривіальними).
Перетином двох
підпросторів V1 і V2
векторного простору V називається
множина всеможливих векторів із V,
що належить одночасно і V1,
і V2. Перетин теж є підпростором
і позначається
![]()
Сумою двох
підпросторів V1 і V2
називається множина векторів вигляду
![]() де
де
![]() Сума теж є підпростором і позначається
V1+V2.
Сума теж є підпростором і позначається
V1+V2.
Теорема. Якщо V1 і V2 – підпростори векторного простору V, то
![]()
Доведення.
В підпросторі
![]() виберемо довільний базис е1,
е2,…, еk
і доповнимо його до базису V1
з одного боку:
виберемо довільний базис е1,
е2,…, еk
і доповнимо його до базису V1
з одного боку:
е1, е2,…,еk, fk+1,…,fp (*1)
і до базису V2 з другого боку:
е1, е2,…,еk, gk+1,…,gs (*2).
Покажемо , що вектори е1, е2,…,еk, fk+1,…, fp, gk+1,…,gs лінійно незалежні.
Припустимо, що ці вектори лінійно залежні:
![]()
Тоді вектор
![]()
належить одночасно і V1, і V2, а, значить, і їх перетину Але тоді він повинен лінійно виражатись через базисні вектори підпростору :
![]()
тобто
![]() .
.
Звідси і з єдиності розкладу вектора а за базисом простору V1 маємо
![]()
Тоді матимемо
![]()
звідки, із лінійної незалежності базисних векторів простору V2 маємо
![]()
Отже, вектори
е1, е2,…,еk,
fk+1,…, fp,
gk+1,…,gs
утворюють лінійно незалежну систему.
Але тоді вони утворюють базис простору
V1+ V2, оскільки,
якщо вектор
![]() то z=x+y,
де
то z=x+y,
де
![]() і, значить, х лінійно виражається
через (*1), а у – через (*2). Але тоді
вектор z лінійно виражається
через вектори
і, значить, х лінійно виражається
через (*1), а у – через (*2). Але тоді
вектор z лінійно виражається
через вектори
е1, е2,…, еk, fk+1,…, fp, gk+1,…,gs.
Таким чином, розмірність підпростору V1+ V2 дорівнює
k+(p-k)+(s-k)=p+s-k.
Але
dimV1=p, dimV2=s,
![]() Тоді
Тоді
dimV1+dimV2=p+s
і
![]()
що й треба довести.
