5. Проверка значимости коэффициентов регрессии.

Очевидно, что один фактор больше влияет на переменную состояния, другой — меньше. Для оценки этого влияния используют проверку значимос­ти каждого коэффициента двумя равноценными способами. В обоих случаях вначале находят дисперсию коэффициентов регрессии по формуле:

(21)

т. е. дисперсии всех коэффициентов равны, поскольку зависят толь­ко от ошибки опыта и числа строк матрицы планирования N.

По первому способу оценку значимости коэффициентов определяется по формуле:

(22)

и условию

(23)

где — абсолютное значение i-гo коэффициента регрессии; — табличное значение критерия Стьюдента, которое находят по числу степеней свободы

f₀ = N (m — 1) и уровню значимости q

— среднеквадратичное отклонение b_i.

По второму способу для проверки значимости коэффициентов регрессии используют доверительный интервал , который, вследствие равенства для всех коэффициентов, одинаков для всех b_i:

(24)

Тогда значимость оценивают, сравнивая абсолютные значения ко­эффициента и доверительного интервала:

(25)

Если выполняются условия (24) и (25), то i-й коэффициент при­знается значимым.

6. Принятие решений.

Если для какого-то коэффициента условия (78) и (80) не выполняются, то соответствующий фактор можно признать незначимым и исключить его из уравнения регрессии.

Однако надо быть осторожным и всегда помнить, что в предвари­тельном эксперименте уже отсеивались незначимые факторы, скорее всего полученная незначимость фактора является следствием неудач­но выбранного интервала варьирования: он был выбран малым. Более правильным является решение повторить эксперимент при расширенном интервале варьирования для иссле­дуемого фактора. Конечно, при этом число опытов, а значит, время эксперимента, возрастает. Иногда половину опытов сохраняют тем, что расширение интервала варьирования проводят только в одну сторону: один (верхний или нижний) уровень остается.

Если фактор остался незначимым после повторения экспери­мента и всех необходимых расчетов, то его (или их) отбрасывают и пе­реходят к оценке адекватности полученной математической модели.

7. Проверка адекватности линейного уравнения регрессии.

При­годность линейного уравнения регрессии для решения задачи поис­ка области оптимума проверяется методом, изложенным в гл. II, § 6. Сравниваются две дисперсии — одна показывает рассеяние средних опытных данных переменной состояния относительно тех значений переменной состояния , которые предсказаны по­лученным линейным уравнением регрессии. Эта дисперсия назы­вается дисперсией адекватности и рассчитывается по формуле:

(26)

где m — число параллельных опытов; N — число строк матрицы планирования; l — число членов в уравнении регрессии, остав­шихся после оценки значимости.

Вторая дисперсия — это ошибка опыта. Адекватность прове­ряют, оценивая отношение

(27)

по критерию Фишера

(28)

для степеней свободы f_ад = N — l, f₀ = N (m — 1) и заданного уровня значимости q. Если выполняется условие (28), то линейное уравнение регрессии признается адекватным, т. е. рассеяние экспе­риментальных данных переменной состояния относительно уравне­ния регрессии того же порядка, что и рассеяние, вызванное случай­ными изменениями в объекте исследования (ошибка опыта)

Таблица 7. Формула расчета ПФЭ2ⁿ

Блоки	Формулы расчета	Обозначения
1	Или	– переменная состояния расчетная); – факторы; – коэффициенты уравнения регрессии; – число факторов; – переменная состояния (экс­периментальная); – транспонированная матри­ца X; – число опытов – построчная дисперсия; –переменная состояния (в параллельных опытах) – расчетные значения крите­рия Кохрена; – число параллельных опытов – табличное значение крите­рия Кохрена; – число степеней свободы; – уровень значимости – ошибка опыта (дисперсия воспроизводимости); – дисперсии коэффициентов; – расчетное значение крите­рия Стьюдента; – среднеквадратичные откло­нения – табличное значение крите­рия Стьюдента; – число степеней свободы; – дисперсия адекватности; – расчетное значение крите­рия Фишера – число степеней свободы
2
3
3а	Условие однородности
4
5
5а	Условие значимости коэффициентов
6
6а	Условие адекватности модели (q, f1,f2)

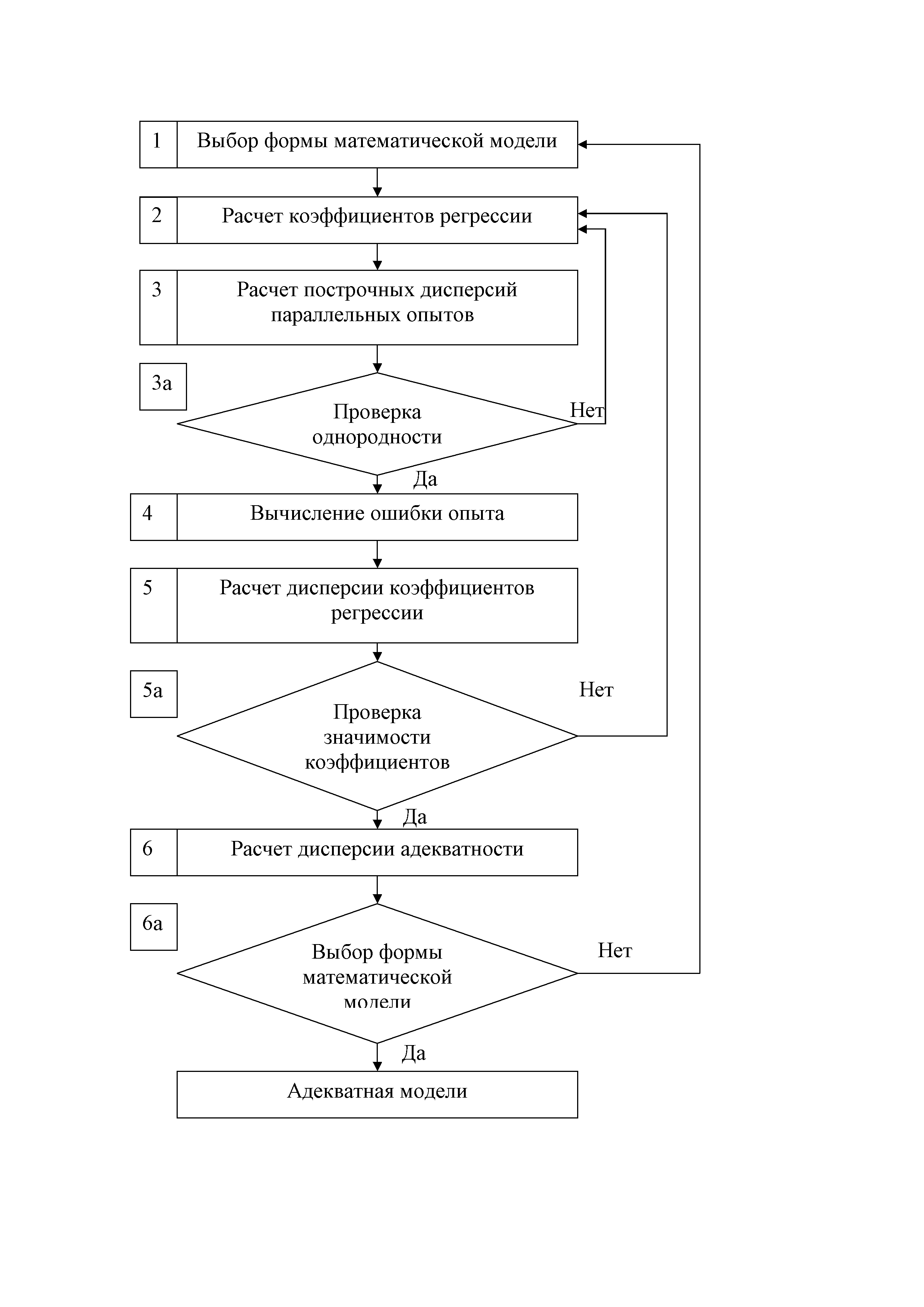
Рис. 4. Алгоритм расчета и анализа мате­матической модели

При расчете F_p предпо­лагается, что > . Од­нако на практике бывает, что . Тогда вывод об адекватности модели мо­жет быть сделан без про­верки условия (23).