Основной эксперимент, планы первого порядка

Задача основного эксперимента — получение матема­тической модели исследуемого объекта, которая используется для оптимизации объекта исследования или для целей аппроксимации. Для получения математической модели, используется факторный эксперимент:

Все факторы объекта исследования вирируются по определенному плану.

Рассмотрим пример построения

Матрица планирования эксперимента для двух факторов на двух уровнях

Таблица 1

Опыты	X0	Планирование		Перемен­ная состоя­ния y
		X1	X2
1	+1	+1	+1	y1
2	+1	-1	+1	y2
3	+1	+1	-1	y3
4	+1	-1	-1	y4

Предположим, что объектом исследования является реактор, в котором выход продукта у за­висит от температуры х₁ и давле­ния х₂ в реакторе. Дополнитель­но известно, что изменение тем­пературы от 60 до 80° С и давле­ния от 1 до 1,5 атм изменяет выход продукта. Обозначим мак­симальные и минимальные значе­ния факторов х₁ и х₂ символами + 1 и -1. Тогда все возможные комбинации факторов при варьировании на двух уровнях (мини­мальном и максимальном) будут определены четырьмя опытами. Такой план эксперимента принято записывать в виде матрицы пла­нирования (табл. 22).

Во второй графе таблицы приведены значения фиктивной пере­менной х₀ (тождественно равной -1 +1), которая понадобится при вы­числении свободного члена полинома. В первой строке таблицы спла­нирован первый опыт, когда факторам х₁ и х₂ придают максимальные значения; во второй строке — когда фактору х₁ придают ми­нимальное значение, а фактору — максимальное, и т. д. Ока­зывается подобное планирование имеет ряд достоинств и поэто­му широко применяется для получения моделей. Например, поль­зуясь планом — табл. 1, можно после проведения эксперимента определить коэффициенты линейного уравнения регрессии

(1)

Сущность факторного эксперимента первого порядка состоит в одновременном варьировании всех факторов при его про­ведении по определенному плану, представлении математической модели (функции отклика) в виде линейного полинома и исследова­нии этой зависимости методами математической статистики.

Уровнем фактора называют определенное значение фактора, которое будет фиксироваться при проведении эксперимента. В пре­дыдущем примере уровнями факторов будут 60 и 80° С для фактора «температура», а также 1 и 1,5 атм— для фактора «давление». Уровнем факторов можно назвать и средние значения рассматриваемых интервалов, т. е. 70° С и 1,25 атм.

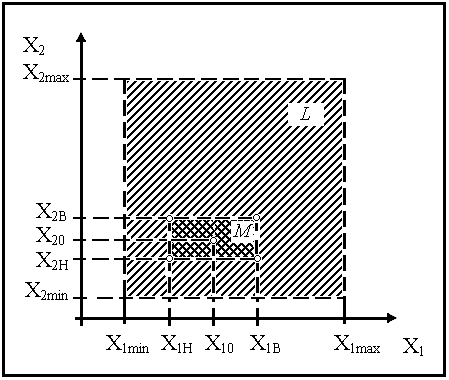
Рис 1 Геометрическая интерпретация области определения факторов L и области проведения эксперимента М.

Эти значения факторов называются нулевыми уровнями, они определяют неко­торую точку факторного про­странства, которая в предвари­тельном эксперименте была оце­нена наилучшей по максимуму (или по минимуму) переменной состояния. Обозначим нулевой уровень i-го фактора, выражен­ного в натуральных единицах (в данном примере в °С и атм), через .

Интервал варьирования. Это такое значение фактора в натуральных единицах, прибав­ление которого к нулевому уров­ню дает верхний, а вычитание — нижний уровень фактора. Обо­значим его

Границы существования факторов - это экстремальные значения, которые могут принимать факторы, не меняя своих физико-химических свойств и не искажая сути исследуемого процесса, Область определения факторов (область L на рис. 1)- это интервал (X_min X_max).

Интервал варьирова­ния факторов должен составлять часть области определения фак­торов, если решается задача оптимизации. Это необходимо для того, чтобы осуществить движение к оптимуму в области- определения факторов. На рис. 1 область проведения эксперимента обозначена буквой М. В задачах же аппроксимации (или интерполяции) ин­тервал варьирования охватывает всю описываемую область, т. е. для двухфакторной задачи верхними уровнями факторов Х₁ и Х₂ являются , , а нижними уровнями — и Тогда область L можно назвать интерполяционной, область М — областью постановки экстремального эксперимента.

Из определений следует, что областей М может быть несколько (в общем случае конечное множество). Можно также предположить несколько областей оптимума. Область определения факторов для данной задачи исследования одна. Обозначение верхних и нижних уровней факторов символами «+1», «—1» фактически соответствует кодированию факторов по формуле

. (2)

Для рассмотренного примера (табл. 22) кодированные значения факторов (верхние и нижние уровни) следующие:

Рис.2. Геометрическая интерпретация плана 2² на плоскости а) – в натуральных координатах, б) в кодированной форме.

Рис. 3. Геометрическая интерпретация плана 3²

Кодирование факторов, по сути, означает переход от системы координат в натуральных единицах (рис. 2, а) к системе координат в кодированной форме (рис. 2, б). Каждая точка факторного про­странства — (+1, +1), (—1, +1), (+1, —1), (—1, —1) — это опыт в исследованиях.

В общем случае эксперимент, в котором реализуются все воз­можные сочетания уровней факторов, называется полным фактор­ным экспериментом (ПФЭ). Если каждый фактор варьируется на двух уровнях, то получается ПФЭ тина 2ⁿ. Для двух факторов (n = 2) число опытов N = 2² =4, что видно из табл. 1 и рис. 2.

Можно осуществлять планирование эксперимента на трех уров­нях (верхний, средний, нижний), тогда ПФЭ будет типа 3ⁿ и для n = 2 общее число опытов будет N = 3² = 9 см. рис. 3.

Этот этап выде­ляют как этап принятия решений перед составлением плана экспе­римента. Построение плана эксперимента начинают с выбора определяющих его характеристик. Обычно первой рас­сматривают область определения факторов. Область определения факторов фиксируется в пред­варительном эксперименте. Для этого используются результаты опытов и теоретические представления о процессе.

Далее из области определения факторов выбором нулевых уров­ней и интервалов варьирования факторов выделяется часть области для планирования эксперимента (область М, рис. 1). Правильный выбор нулевых уровней (центра эксперимента) и интервалов варьи­рования факторов имеет решающее значение для действенности математической модели.

Идеальным случаем при выборе нулевых уровней факторов яв­ляется «попадание» центра эксперимента в область оптимальных значений переменной состояния. Но это возможно лишь при очень высоком уровне априорной информации.

Если имеет­ся некоторый опыт управления объектом исследования, можно при­нять в качестве нулевых уровней те величины факторов, которые дали наилучшее значение переменной состояния.

Но это может привести к получению лишь локального оптимума при нескольких экстремумах функции отклика,

Основное требование к интервалу варьирования состоит в том, чтобы он превышал удвоенную квадратическую ошибку фактора:

(3)

где — среднеквадратическое отклонение фактора ; — интервал варьирования; — область определения фактора.

Это требование связано с тем, что интервал между двумя сосед­ними уровнями должен значимо (неслучайно) влиять на перемен­ную состояния. Обычно интервал варьирования выбирается на ос­новании априорной информации (или интуитивно) и затем уточ­няется (если он выбран неудачно) после получения математической модели. Повторение эксперимента, резко увеличивает число опытов. Удачный выбор интервала варьирования факторов гарантирует получение достоверной математиче­ской модели объекта.

Определенные сведения о нулевых уров­нях и интервалах варьирования получаются на этапе предва­рительного эксперимента.

Пример 1.

Рассмотрим процесс ионообменного разделения смесей группы редкозе­мельных элементов растворами иминодиуксусной кислоты. Пере­менная состояния—содержание (в %) неодима в выходном рас­творе.

Предварительный эксперимент выделил два фактора — концентрацию (в вес. %) входного раствора Х₁ и рН раствора Х₂. Область определения фактора X₁ находилась из следующих услови.

Известно, что при X₁ > 3 работать нельзя, так как это предел растворимости данного вещества при нормальной температуре. Таким образом, . При выборе нижней границы области определения фактора учитывалось то, что чем ниже концентрация, тем дольше идет процесс. При время протекания процесса находится еще в допустимых пределах; дальнейшее снижение его уже нецелесообразно.

При выборе области определения Х₂ исходили из теоретического положения, что ионообменное разделение происходит благодаря одновременному присутствию в системе двух соединений: моно- и ди-комплексов. Предварительный эксперимент показал, что при рН < 3 кислота находится в недиссоциированном состоянии, а при рН > 8 оба соединения разрушаются. Следовательно, , .

В качестве нулевых уровней были приняты значения X1₀ = 1,5, Х2₀ = 7. В точке факторного пространства с такими координатами был получен наилучший результат предварительного эксперимен­та. Важно также то, что она лежит внутри области определения факторов.

Результаты предварительных опытов, явилось следующее:

1. точность фиксирования факторов средняя (по результатам ряда опытов);

2. поверхность отклика линейная (по однофакторным экспери­ментам);

3. диапазон изменения переменной состояния небольшой.

Рослее предварительного эксперимента пришлось выбрать широ­кий (до 20% от области определения) интервал варьирования, чтобы его изменение было заметно по изменению переменной состояния: ,