5. Метод Койтера исследования нелинейного послебифуркационного процесса выпучивания (нагружения). Пусть реакция в упругой пружине (рис. 9.13):

(9.15)

т.е. зависимость носит нелинейный характер.

а) б)

Рис. 9.13

Тогда уравнение равновесия (9.3) примет вид

(9.16)

откуда либо , либо , и тогда равно нулю выражение в квадратной скобке. Второе условие приводит к соотношению, которое позволяет установить зависимость между силой и перемещением в процессе нагружения элемента:

(9.17)

Если , то имеем кривые зависимости с симметричной бифуркацией (рис. 9.13,а). Предположим, что с развитием выпучивания и увеличением перемещения в пружине при возникают пластические деформации. Тогда вместо (9.3) при имеем:

откуда

(9.18)

и с ростом нагрузка будет падать (рис. 9.13,а).

В реальных системах переход к пластической стадии деформирования осуществляется на графике от плавно с экстремальной предельной точкой.

Если , то согласно (9.17) имеем симметричную неустойчивую бифуркацию, характерную для сжатых неупругих стержней и пластины (рис. 9.13,б).

Пусть теперь

( ).

Тогда, согласно (9.12), имеем:

откуда при получаем:

(9.19)

При >0, <0, <0 зависимость (9.19) имеет несимметричный вид (рис. 9.14,а). Прогибы после бифуркации растут при падающей нагрузке. Такая точка бифуркации называется неустойчивой. Она характерна для упругих оболочек.

Если >0, >0, <0, то бифуркация будет также несимметричной (рис. 9.14,б).

а) б)

Рис. 9.14

Задача Эйлера об устойчивости сжатого стержня

Познакомившись с концепцией устойчивости и модельными задачами, мы можем теперь перейти к рассмотрению задач устойчивости упруго сжатого стержня (рис. 9.15).

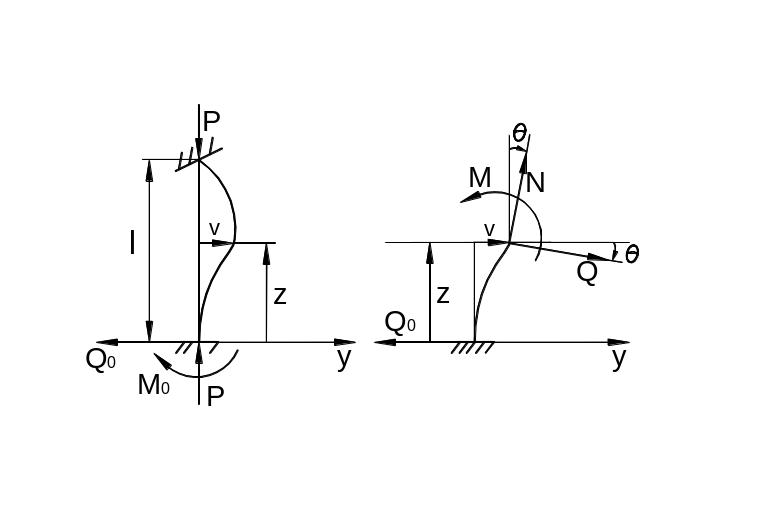
а) б)

Рис. 9.15

Считаем стержень идеально прямым и сжатым центрально приложенными силами (рис. 9.15,а). Следуя методу Эйлера, будем считать исходное состояние равновесия упругого стержня устойчивым, если после статического приложения и снятия возмущающей силы при постоянных внешних сжимающих силах стержень возвращается к своей исходной прямолинейной форме равновесия. В противном случае состояние равновесия считаем неустойчивым.

Допустим, что стержень остался в изогнутом состоянии (рис. 9.15,б). Отсечём часть стержня на расстоянии z от начала координат, считая угол поворота сечения малой величиной, и составим уравнения равновесия:

(9.20)

Изгибающий момент в поперечном сечении, согласно (6.9), равен:

. (9.21)

Приравнивая выражения моментов (9.20), (9.21), находим:

(9.22)

Дифференцируя (9.22) по , получим:

(9.23)

дифференцируя (9.23) по , приходим к уравнению изогнутой оси потерявшего устойчивость стержня четвёртого порядка:

. (9.24)

Введём обозначение:

. (9.25)

Тогда уравнения (9.22), (9.24) можно записать в виде

(9.26)

(9.27)

Общее решение уравнения (9.26) имеет вид:

(9.28)

В него входят четыре произвольные постоянные .

Общее решение уравнения (9.27):

(9.29)

В него входят четыре произвольные постоянные .

Производные:

(9.30)

Используя (9.30), из (9.21), (9.23) находим:

(9.31)

Постоянные находятся из граничных условий. Для шарнирно закреплённого по концам стержня при и имеем условия:

Для стержня, защемлённого при и свободного от закрепления при , должны выполняться условия:

при ,

при .

Если на незакреплённом конце при действуют внешние момент и поперечная сила , то

При любом закреплении концов стержня мы имеем четыре граничных условия (по два на каждом краю), которые при подстановке в них выражений (9.28), (9.29) приводят к системе четырёх однородных алгебраических уравнений вида:

или

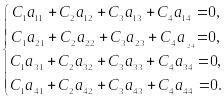(9.32)

Система уравнений (9.32) имеет отличные от нуля решения только при условии, что её определитель:

откуда, после его раскрытия, находим некоторое числовое значение :

,

где - некоторое число. Возводя обе части полученного равенства в квадрат и используя обозначение (9.25), получаем формулу для критического значения силы (нагрузки бифуркации) Эйлера:

, (9.33)

где - приведённая длина Ясинского, - коэффициент приведения длины стержня к длине шарнирно опёртого по концам стержня.

Соответствующее критическое напряжение Эйлера:

(9.34)

где

- (9.35)