Расчёты движущихся деталей при заданных ускорениях
Определение напряжений и перемещений при заданных ускорениях основано на приведении задач динамики к задачам статики с помощью известного из курса теоретической механики принципа Даламбера (метода кинетостатики). Напомним, что этот принцип состоит в следующем: если в любой момент времени к каждой материальной точке данной системы приложить силу инерции этой точки, то эти силы инерции будут уравновешиваться заданными силами, действующими на систему, и реакциями связей, т.е. система может рассматриваться как находящаяся в состоянии покоя (или равномерного прямолинейного движения). Сила инерции равна произведению массы материальной точки на её ускорение и направлена в сторону, противоположную ускорению.
Расчет поступательно движущихся систем
Определим напряжения в канате грузоподъемного механизма, к которому подвешен груз массой m (рис. 15.13).
При
равномерном подъеме с постоянной
скоростью ускорение движения груза
равно нулю, поэтому напряжения в канате
такие же, как и в том случае, когда груз
висит на канате в состоянии покоя, т.е.
,
где g
-
ускорение силы тяжести.
Рис. 15.13
Во время разгона движение груза неравномерно, и в канате появляются дополнительные напряжения, для определения которых мысленно остановим груз и приложим к нему силу инерции. Эта сила направлена в сторону, противоположную движению груза и равна
,
где
v
- скорость подъема;
-
ускорение.
Наибольшее усилие в канате соответствует моменту максимального ускорения груза во время разгона:
.
Следовательно, максимальное напряжение в канате при подъеме груза
.
больше
напряжений при статическом приложении
груза
в
раз;
коэффициент
называется динамическим коэффициентом.
Таким образом, для уменьшения растягивающего усилия в канате необходимо обеспечить плавное увеличение скорости подъема, так как при больших ускорениях напряжения в канате могут стать значительными. График изменения скорости в период разгона должен иметь вид, представленный на рис. 15.14. Тангенс наибольшего угла наклона касательной к этой кривой определяет максимальное ускорение движения груза во время подъема.
Рис. 15.14
При
опускании груза в начале движения
величина
в
выражении для
будет
иметь отрицательный знак. Следовательно,
напряжения в канате в этом случае будут
меньше напряжений от статического
действия груза m.
Если канат длинный, то следует учесть массу самого каната и силы инерции его частиц. В этом случае опасным будет верхнее сечение каната, усилие в котором
,
где
x
- длина каната;
-
плотность материала каната.
Рассмотрим горизонтальный брус, поднимаемый вверх силой S, приложенной посредине бруса (рис. 15.15, а).
Интенсивность
полной погонной нагрузки, состоящей из
собственного веса q
бруса
и инерционной нагрузки
,
определяется по формуле (рис. 15.15, б,
в)
или
,
где G - вес бруса, - ускорение бруса.
Рис. 15.15
Сила S и нагрузка qсумм вызывают изгиб бруса. Эпюры изгибающих моментов M и поперечных сил Q показаны на рис. 15.15, г, д.
Напряжения в тонкостенном вращающемся кольце
Рассмотрим
случай вращения тонкостенного кольца
(
)
с постоянной угловой скоростью
вокруг
оси, перпендикулярной к плоскости кольца
(рис. 15.16, а).
При
вращении кольца каждый его элемент
движется с центростремительным ускорением
.
Силы инерции направлены в сторону,
противоположную ускорениям, и при
постоянном сечении распределены
равномерно вдоль кольца. Интенсивность
сил инерции, т.е. сила инерции, приходящаяся
на единицу длины кольца,
.
Здесь
-
плотность материала, F
- площадь сечения, а R
- радиус средней линии кольца.
Кольцо теперь можно рассматривать как неподвижную плоскую раму, нагруженную равномерно распределенными радиальными силами интенсивностью q.
Рассекая кольцо любой диаметральной плоскостью на две части, приложим в сечениях осевые силы N и изгибающие моменты X1.
Рис. 15.16
Проектируя все силы, действующие на полукольцо, на направление оси y, получаем
.
Отсюда
.
Подставляя в это выражение значение q, находим
.
Для определения неизвестного X1 составим каноническое уравнение
,
коэффициенты которого вычислим способом Мора.
Изгибающий момент в текущем сечении полукольца от силы N и распределенной нагрузки q (см. рис. 15.16, б)
,
а
от единичной пары
.
Следовательно,
и
поэтому X1=0,
т.е. изгибающие моменты во всех поперечных
сечениях кольца равны нулю. Этот результат
объясняется тем, что при вращении вокруг
центра кольцо сохраняет свою форму и
никаких изгибных деформаций не испытывает;
увеличивается только его диаметр.
Таким образом, нормальные напряжения в поперечном сечении кольца
Например, в стальном кольце ( =7850 кг/м3) радиуса R=50 см при n=2500 об/мин растягивающее напряжение
Итак,
напряжения во вращающемся кольце зависят
только от окружной скорости
и
плотности материала, но не зависят от
площади его поперечного сечения. Поэтому
увеличением размеров сечения нельзя
уменьшить напряжения в тонкостенном
вращающемся кольце.
Рассмотрим теперь случай равномерного вращения тонкостенного кольца вокруг его горизонтальной оси x.
Различные элементы кольца находятся на разных расстояниях от оси вращения, и поэтому силы инерции распределены неравномерно по длине кольца (рис. 15.17, a):
.
Максимальная
интенсивность
.
Следовательно,
.
В сечениях вдоль вертикальной оси симметрии кольца будут действовать только изгибающие моменты X1, а перерезывающие силы Q и нормальные силы N равны нулю. В отсутствии нормальных сил N в этих сечениях легко убедиться, спроектировав все силы, действующие на левое или правое полукольцо, на горизонтальную ось симметрии.
Представим эквивалентную систему, как показано на рис. 15.17, б. Изгибающий момент в текущем сечении кольца от внешней нагрузки
,
а от единичной пары .
Рис. 15.17 Рис. 15.18
Составим каноническое уравнение
,
Коэффициенты
и
этого
уравнения:
;
.
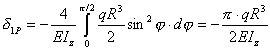Следовательно,
.
Итак, изгибающий момент в текущем сечении рамы
.
Эпюра
изгибающих моментов представлена на
рис. 15.18. Опасными являются сечения A
и B
кольца, так как в этих сечениях кроме
изгибающих моментов
действуют
наибольшие растягивающие нормальные
силы
.
Максимальные напряжения в раме
,
где
-
момент сопротивления изгибу, а F
- площадь поперечного сечения кольца.
Расчет равномерно вращающегося прямого бруса
Предположим, что прямой брус постоянного поперечного сечения с подвешенным грузом равномерно вращается вокруг оси, перпендикулярной плоскости чертежа (рис. 15.19). Определим напряжения в сечениях бруса.
Рис. 15.19
При отсутствии вращения напряжения в поперечных сечениях бруса изменяются по линейному закону:
,
где - плотность материала бруса; F - площадь поперечного сечения; G - вес груза.
Применяя принцип Даламбера, приложим к каждому элементу бруса силу инерции, равную массе этого элемента, умноженной на его центростремительное ускорение. Динамическая продольная сила будет равна:
.
После интегрирования динамически напряжения определяются по следующей формуле:
.
Напряжения изменяются по квадратичному закону и достигают максимума на оси вращения
.
Перемещение текущего сечения бруса
.
Полагая
в этом выражении
,
находим удлинение всего бруса, вызванное
его вращением.
При отсутствии груза следует исключить в формулах величину G.
При вращении стержня относительно вертикальной оси (рис. 15.20) полученные выше формулы для динамических усилий, напряжений и перемещений нетрудно модифицировать. Так, например, динамические напряжения будут равны:
Рис. 15.20
Вращающиеся рамы
Рассмотрим несколько примеров расчета вращающихся рам.
Стержень
регулятора с прикрепленным к нему грузом
массой Q
вращается вокруг оси О-О
(рис. 15.21, а)
с постоянной угловой скоростью
.
Построим эпюру изгибающих моментов,
полагая, что масса рамы мала по сравнению
с массой груза.
Сила
инерции груза
.
Рассматривая силу инерции груза как единственную внешнюю нагрузку на брус, строим эпюру изгибающих моментов (рис. 15.21, б). Максимальный изгибающий момент
.
Рис. 15.21
Рассмотрим более сложный пример. Прямоугольная рама постоянного сечения (рис. 15.22, а) вращается вокруг вертикальной оси симметрии с угловой скоростью . Определим изгибающие моменты в сечениях рамы, вызванные ее вращением.
На
горизонтальных элементах рамы
интенсивность сил инерции изменяется
по линейному закону
.
На вертикальных элементах интенсивность
инерционной нагрузки постоянна и равна
(направление
этих сил показано на рис. 15.22,б
стрелками).
Рис. 15.22
Основную
систему выберем, рассекая раму по
вертикальной оси симметрии. Из условия
симметрии системы относительно
вертикальной и горизонтальной осей
следует, что в сечениях по вертикальной
оси симметрии перерезывающие силы равны
нулю, осевые силы согласно уравнению
будут
.
Для определения неизвестных изгибающих моментов X1 в этих сечениях составим каноническое уравнение
,
коэффициенты которого вычислим способом Верещагина. Перемножая эпюры от внешних и единичных сил (рис. 15.22), получаем
.
Подставляя
значения
и
в
каноническое уравнение и решая его
относительно X1,
имеем X1=qa2/36.
Суммируя изгибающие моменты в сечениях рамы от заданной нагрузки и X1, строим эпюру изгибающих моментов (рис. 15.23). Опасными являются сечения рамы, расположенные на горизонтальной оси симметрии, изгибающие моменты в которых
.
Рис. 15.23
Вопросы для самопроверки
- Дайте определение ударных нагрузок.
- Дайте определение инерционных нагрузок.
- Что такое коэффициент динамичности нагрузки?
- Условие прочности при динамических нагрузках.
- Может ли быть коэффициент динамичности нагрузки меньше единицы?
- Как произвести расчёт на прочность тонкостенного вращающегося кольца?
- Как определить напряжения и перемещения, возникающие при ударном действии нагрузки?
- Как определяется величина динамического коэффициента, если высота падения ударяющего тела значительно больше статического перемещения бруса в точке удара?
- При забивке деревянной сваи молот копра весом G падает с высоты h. Какие напряжения возникают в сечении сваи?
1) статические напряжения;
2) динамические напряжения.
- Напряжения в сечениях сваи рассчитывают по формуле:
1)
;
2)
;
3)
;
4)
.
- Условия динамической прочности?
1.
2.
3.
4.
- Что такое динамический коэффициент?
1. Характеризует увеличение статических напряжений в случае динамического воздействия.
2. Коэффициент, зависящий от массы сооружения.
3. Характеризует угловое ускорение движения.
4. Характеризует величину ударной нагрузки.
- Какие напряжения относятся к динамическим?
1. Вызванные кручением.
2. Вызванные изгибом.
3. Вызванные при ударе.
4. Вызванные растяжением.
- Какие напряжения относятся к динамическим?
1. Вызванные растяжением.
2. Вызванные кручением.
3. Вызванные силами инерции, обусловленные ускорением.
4. Вызванные изгибом.
- Ударная нагрузка – это:
1. нагрузка при соударении тел;
2. нагрузка при трении;
3. нагрузка при ударе вертикально движущихся тел.
- Инерционная нагрузка – это:
1. нагрузка при торможении тел;
2. нагрузка в начале движения;
3. нагрузка при движении тела с ускорением.
- Условие прочности при ударе:
1.
;
2.
;
3.
.
- Коэффициент динамичности нагрузки всегда меньше 1.
1. да;
2. нет;
3. зависит от направления удара.
- Напряжение при ударе зависит от кинетической энергии соударяющихся тел.
1. нет;
2. да;
3. при учете принципа Даламбера.
