
- •Раздел четвертый теплообмен излучением
- •Тема 14 Основные положения лучистого теплообмена
- •14.1 Описание процесса
- •14.2 Виды лучистых потоков
- •14.3 Законы теплового излучения
- •Виды лучистых потоков.
- •Тема 15 Теплообмен излучением меду твердыми телами, разделенными прозрачной средой
- •15.1 Методы исследования лучистого теплообмена
- •15.2 Теплообмен излучением в системе тел с плоскопараллельными поверхностями
- •15.3 Излучательная способность твердых тел и методы ее определения
- •15.4 Теплообмен излучением между телом и его оболочкой
- •15.5 Теплообмен излучением между двумя телами, произвольно расположенными в пространстве. Угловые коэффициенты излучения
- •15.6 Геометрические свойства лучистых потоков
- •15.7 Методы определения угловых коэффициентов излучения
- •Тема 16 Теплообмен в поглощающих и излучающих средах
- •16.1 Уравнение переноса энергии в поглощающей среде
- •16.2 Особенности излучения газов и паров
- •16.3 Сложный теплообмен
- •16.4 Критерии радиационного подобия
15.4 Теплообмен излучением между телом и его оболочкой
Изучающая система без экранов. Рассмотрим два тела, из которых одно находится внутри другого. Первое – выпуклое, второе – вогнутое. Размеры тела заданы F1 и F2, поглощательные способности A1 и A2, а также температуры поверхностей T1 и T2, причем T1 >T2. Используя уравнение для результирующей плотности теплового потока, при наличии диатермичной среды
![]() ,
,
где
![]() - средний угловой коэффициент излучения.
- средний угловой коэффициент излучения.
О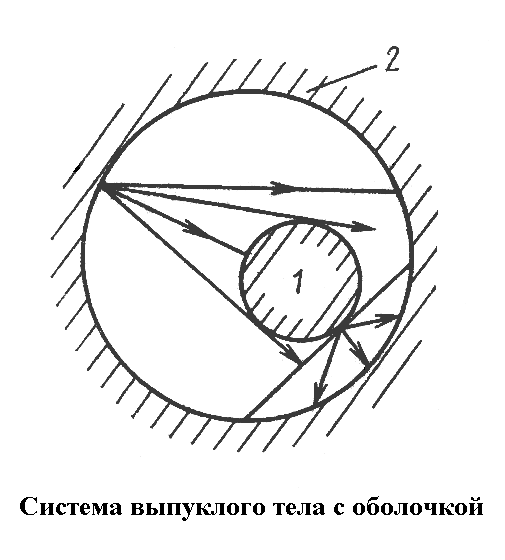 н
характеризует часть потока эффективного
излучения, который попадает со второго
тела на первое по отношению к полному
потоку эффективного излучения второго
тела. Угловой коэффициент
н
характеризует часть потока эффективного
излучения, который попадает со второго
тела на первое по отношению к полному
потоку эффективного излучения второго
тела. Угловой коэффициент
![]() ,
так как вся излучаемая энергия первого
тела попадает на второе тело. Угловой
коэффициент
,
так как вся излучаемая энергия первого
тела попадает на второе тело. Угловой
коэффициент
![]() ,
так как тело выпуклое. Величина
,
так как тело выпуклое. Величина
![]()
Для определения потока результирующего излучения используем метод сальдо
 ,
,
 .
.
Учитывая, что при стационарном режиме результирующие потоки равны
 .
.
Потоки собственного излучения могут быть выражены по закону Стефана-Больцмана через заданные температуры
 ;
;
 .
.
С учетом вышеуказанного, получаем
 .
.
Для определения неизвестных значений
положим временно, что температуры тел
1 и 2 одинаковы. В этом случае
![]() .
Знаменатель не может быть равен нулю,
.
Знаменатель не может быть равен нулю,
![]() ,
Т1≠0, Т2≠0. Тогда,
,
Т1≠0, Т2≠0. Тогда,
![]() .
Откуда
.
Откуда
 .
.
Средний угловой коэффициент превращается в чисто геометрическую характеристику.
Выражение для результирующего потока излучения примет вид
 .
.
Введем понятие приведённой излучательной способности системы, Вт/(м2К4)
 .
.
Тогда, выражение для результирующего потока излучения
 .
.
Рассмотрим частные случаи.
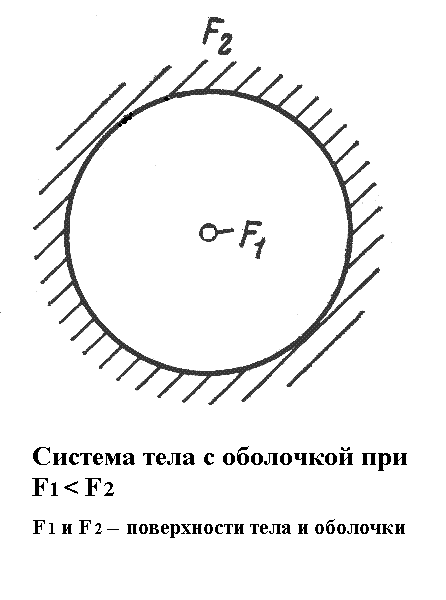
Поверхности тел примерно равны,
 .
.

Угловой коэффициент![]() .
Это означает, что вся энергия с тела 1
попадает на тело 2. В результате, приходим
к решению, полученному для плоскопараллельной
системы тел
.
Это означает, что вся энергия с тела 1
попадает на тело 2. В результате, приходим
к решению, полученному для плоскопараллельной
системы тел
 .
.
2) Одно тело мало по сравнению с другим,
т.е.
![]() <<F2.
<<F2.
В этом случае
![]() с1,2
с1,2![]() с1.
Следовательно, результирующий тепловой
поток
с1.
Следовательно, результирующий тепловой
поток
 .
.
Теплообмен при наличии экранов. Снижение теплообмена при наличии экранов между телом и оболочкой в отличие от случая плоской системы зависит от расположения их относительно излучающего тела, так как в зависимости от этого изменяются угловые коэффициенты излучения. Экранирование оказывается наиболее эффективным, если экран помещается вблизи тела, имеющего более высокую температуру.
а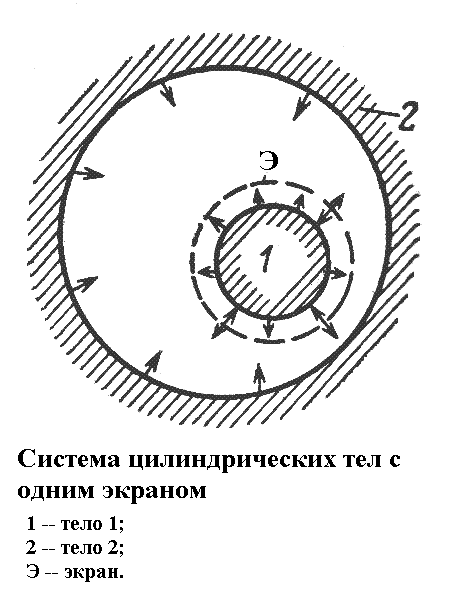 )
один экран
)
один экран
Применительно к системам «тело 1 - экран» и «экран – тело 2» можно записать для потоков результирующего излучения следующие уравнения.
Если положить, что в общем случае
коэффициенты поглощения первого тела
![]() ,
тогда уравнения будут выглядеть так
,
тогда уравнения будут выглядеть так
 ,
,
 ,
,
где приведенные поглощенные способности выражаются следующими зависимостями:

 .
.
При стационарном тепловом режиме
![]() .
.
Используя закон Стефана-Больцмана можно найти независимую температуру экрана:
 .
.
Результирующий поток излучения тогда определяется:
 ,
,
 .
.
Здесь
 ;
;
 ,
,
c0 – коэффициент излучения абсолютно черного тела,
А1,2, c1,2 - относятся к рассматриваемой излучающей системе без экрана.
Второе слагаемое
![]()
характеризует тепловое сопротивление лучистому теплообмену, обусловленное наличием экрана.
б) произвольное число экранов
Рассматривается как совокупность систем последовательно установленных экранов. Это позволяет применить к ним зависимости, полученные для тела с оболочкой при наличии одного экрана.
В итоге получим окончательное выражение для потока результирующего излучения
 ,
,
где приведенный коэффициент поглощения рассматриваемой излучающей системы
 .
.
Видно, что тепловое сопротивление теплообмену излучением возрастает пропорционально числу установленных экранов.
