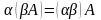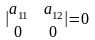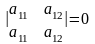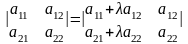- •I. Линейная алгебра Лекция № 1. § 1. Матрицы.
- •Линейные операции над матрицами. Сложение матриц
- •Разность матриц
- •Произведение матрицы на число
- •Произведение матриц
- •Лекция № 2. § 2. Определители. Определитель второго порядка
- •Свойства определителя второго порядка
- •Определитель третьего порядка
- •Вычисление определителя третьего порядка.
- •Определители высших порядков
- •Системы линейных алгебраических уравнений (слау). Лекция № 3. Слау. Решение систем линейных уравнений методом Крамера.
- •Решение систем линейных уравнений методом Крамера.
- •Теорема. (Правило Крамера):
- •Система трех линейных уравнений с тремя неизвестными.
- •Лекция № 4. Метод Гаусса. Решение систем линейных уравнений методом Гаусса.
- •Лекция № 5. Обратная матрица. Матричный способ решения систем. Обратная матрица
- •Матричный способ решения систем
Разность матриц
Определение: Разностью двух матриц называется матрица той же размерности, что и исходные, каждый элемент которой определяется как разность соответствующих элементов матриц.
Пусть
и
.
Тогда
,
где
 ,
,
.
,
,
.
Разность матриц
А и В обозначается символом
 .
.
Замечание 1.
А, В, С – матрицы одинаковых размеров.
Замечание 2.
Разность матриц
можно определить также следующим
образом:
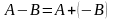 ,
где
,
где
 - матрица, противоположная матрице В.
- матрица, противоположная матрице В.
Произведение матрицы на число
В результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на число.
Пусть
,
k – число. Тогда
такая, что
 (17) (
,
).
Обозначения:
(17) (
,
).
Обозначения: или
или
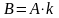 .
.
Пример 3.
Найти матрицу
3А-2В, если
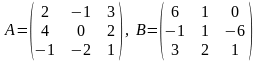
Решение
Имеем
 ,
,
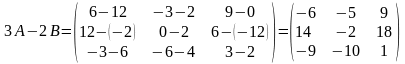
Справедливы следующие свойства
А, В – матрицы.
, - числа.
Произведение матриц
Определение:
Пусть
,
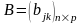 .
Тогда
.
Тогда
 ,
такая, что
,
такая, что
 ,
,
,
,
,
,
 .
.
Произведение
матрицы А на матрицу В обозначают
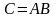 .
.
Следует запомнить, что операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Следует запомнить.
Из определения произведения матриц следует, что элемент матрицы АВ, стоящий в i-й строке и k-м столбце, равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.
Замечание 1.
Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют.
Замечание 2.
Если матрицу А
можно умножить на матрицу В, а В
можно умножить на А, то, вообще
говоря,
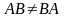 .
.
Пример 4.
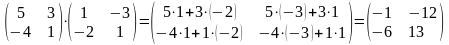
Пример 5.
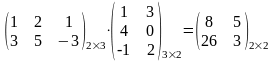
Пример 6.
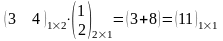
Справедливы следующие свойства умножения матриц:

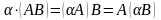
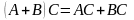
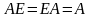 ,
А – квадратная матрица, Е -
единичная матрица того же порядка.
,
А – квадратная матрица, Е -
единичная матрица того же порядка.
Лекция № 2. § 2. Определители. Определитель второго порядка
Определение:
Определителем 2-го порядка называют
число, которое получается из элементов
квадратной матрицы
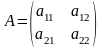 по указанному правилу.
по указанному правилу.
Определитель
второго порядка:
 .
.
Обозначение
определителя:
 .
Определитель матрицы А также называют
ее детерминантом.
.
Определитель матрицы А также называют
ее детерминантом.
Замечание
Вычислить определитель 2-го порядка означает найти разность из произведения элементов, стоящих на главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) и произведения элементов, находящихся на побочной, диагонали.
Пример 1.
Вычислить:

Свойства определителя второго порядка
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|