
- •9. Дифференциальные уравнения
- •9.1. Дифференциальные уравнения первого порядка Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.2. Уравнения с разделяющимися переменными Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.3. Однородные дифференциальные уравнения Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.4. Линейные дифференциальные уравнения первого порядка. Уравнение я. Бернулли Краткие теоретические сведения
- •Метод и. Бернулли
- •Метод Лагранжа (метод вариации произвольной постоянной)
- •Уравнение я. Бернулли
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •Интегрирующий множитель
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.6. Дифференциальные уравнения второго и более высоких порядков, допускающие понижение порядка Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.7. Линейные однородные уравнения с постоянными коэффициентами (лоду) Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.8. Линейные неоднородные уравнения с постоянными коэффициентами второго и более высоких порядков (лнду) Краткие теоретические сведения
- •Метод вариации произвольных постоянных (метод Лагранжа)
- •Метод неопределенных коэффициентов
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.9. Приложение дифференциальных уравнений в экономике Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задачи для самостоятельной работы
Интегрирующий множитель
Если условие (5.4) не выполняются, то ДУ (5.1) не является уравнением в полных дифференциалах.
Такое
уравнение иногда можно свести к ДУ в
полных дифференциалах умножением его
на некоторую функцию
![]() ,
которая называется интегрирующим
множителем.
,
которая называется интегрирующим
множителем.
Если у данного уравнения существует интегрирующий множитель, зависящий только от , то он находится по формуле:
 ,
,
где
отношение
 должно являться функцией только от
.
Аналогично, интегрирующий множитель,
зависящий только от
,
определяется по формуле:
должно являться функцией только от
.
Аналогично, интегрирующий множитель,
зависящий только от
,
определяется по формуле:
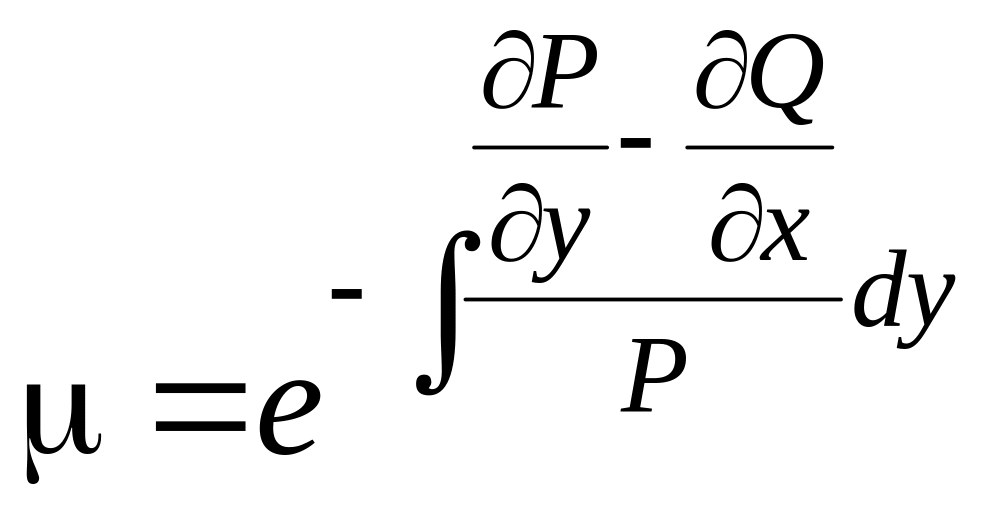 ,
,
где
отношение
 должно являться функцией только от
(отсутствие
в этих отношениях в первом случае
,
а во втором
является признаком существования
интегрирующего множителя рассматриваемого
вида).
должно являться функцией только от
(отсутствие
в этих отношениях в первом случае
,
а во втором
является признаком существования
интегрирующего множителя рассматриваемого
вида).
Примеры решения типовых задач
Пример 1. Найти общий интеграл уравнения в полных дифференциалах
![]() .
.
Решение.
Здесь
![]() .
Так как
.
Так как
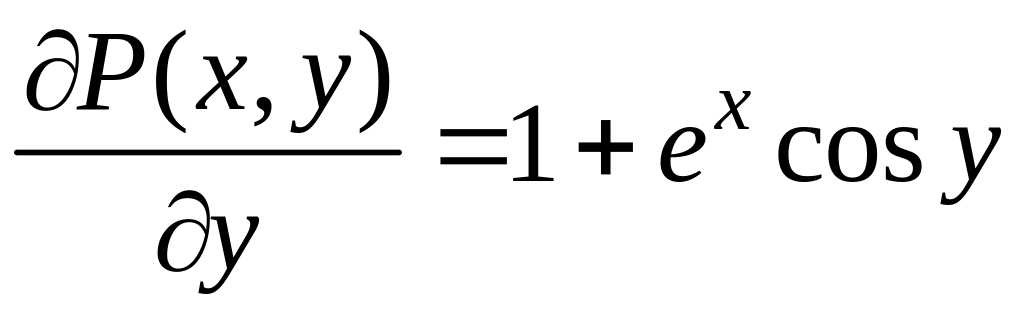 и
и
 ,
то выражение
,
то выражение
![]() является полным дифференциалом некоторой
функции
.
При этом
является полным дифференциалом некоторой
функции
.
При этом
![]() и
и
![]() – непрерывные функции. Тогда
– непрерывные функции. Тогда
1)
![]() и 2)
и 2)
 .
.
Найдем функцию , интегрируя по левую и правую части равенства 1, получим:
![]() .
.
Чтобы найти , продифференцируем последнее выражение по :
![]() .
.
Учитывая равенство 2, запишем уравнение
![]() ,
,
откуда находим:
 .
.
Подставляя найденное в выражение для функции , получаем:
![]() .
.
Таким образом, общий интеграл уравнения имеет вид:
![]() .
.
Пример
2. Найти
частное решение уравнения
![]() ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
![]() .
.
Решение. Запишем данное уравнение в виде:
![]() .
.
Имеем:
![]() ,
,
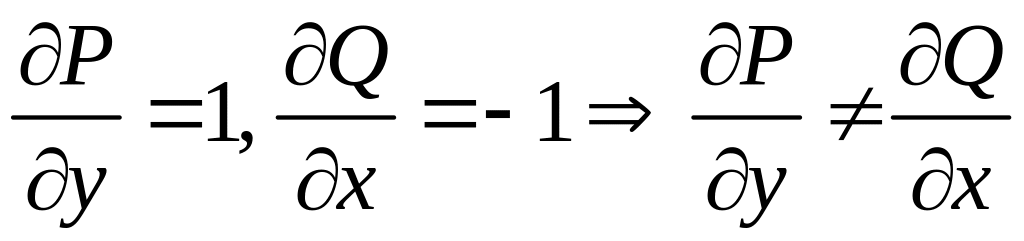 .
.
Значит, данное уравнение не является ДУ в полных дифференциалах. Используем интегрирующий множитель. Запишем отношение
 .
.
Поэтому данное уравнение имеет интегрирующий множитель, зависящий только от .
Найдем этот интегрирующий множитель:
 .
.
Умножим
исходное уравнение на
![]() ,
получим уравнение:
,
получим уравнение:
 ,
,
которое,
как нетрудно убедиться, уже является
ДУ в полных дифференциалах. Действительно,
имеем
![]()
 .
.
Следовательно,
левая часть полученного уравнения имеет
вид
![]() .
Таким образом,
.
Таким образом,
1)
![]() и 2)
и 2)
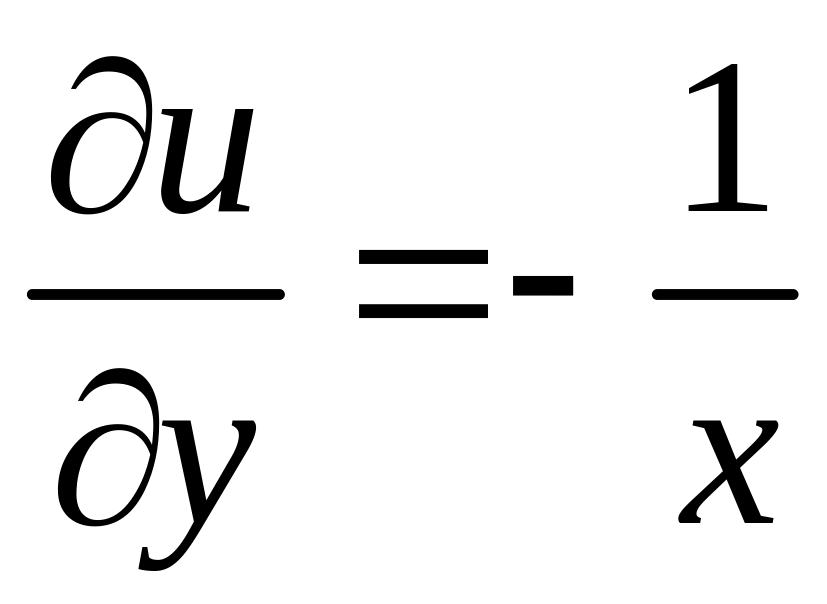 .
.
Интегрируя первое из этих равенств по , находим:
![]() .
.
При
вычислении интеграла
![]() использовали метод интегрирования по
частям:
использовали метод интегрирования по
частям:
 .
.
Найдем производную по от полученной функции:
 .
.
Применяем равенство 2, получаем:
![]() .
.
Следовательно, общий интеграл имеет вид:
![]() .
.
Найдем
частное решение, удовлетворяющее
начальным условиям, т.е. подставим в
общий интеграл
![]() ,
получим:
,
получим:
![]() .
.
Получаем частное решение
![]() .
.
Задания для самостоятельной работы
n9.14. Найти общий интеграл ДУ:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
n9.15. Найти общий интеграл ДУ, используя интегрирующий множитель:
а)
|
б)
|
в)
|
г) |
д) |
е)
|
ж)
|
з)
|
n9.16. Решить задачу Коши для данных ДУ:
а)
|
б)
|
в)
|
г) |
д) |
е)
|
ж) |
з)
|
n9.17. Решить ДУ различных типов, найти частное решение, удовлетворяющее начальным условиям там, где необходимо:
а)
|
б)
|
в) |
г)
|
д)
|
е)
|
ж)
|
з)
|
Ответы

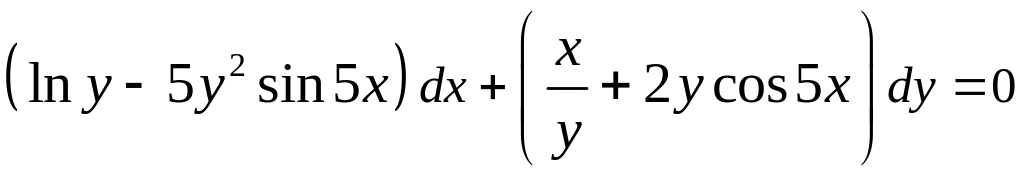 ;
; ;
;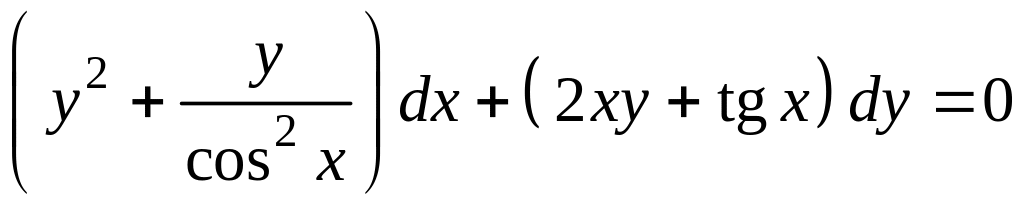 .
. ;
; ;
; ;
; ;
; ;
;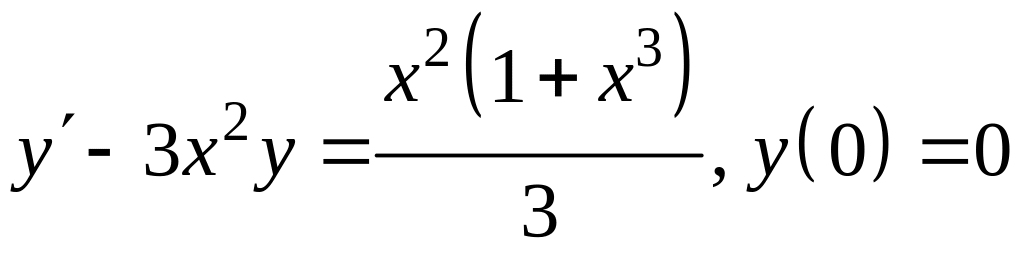 ;
;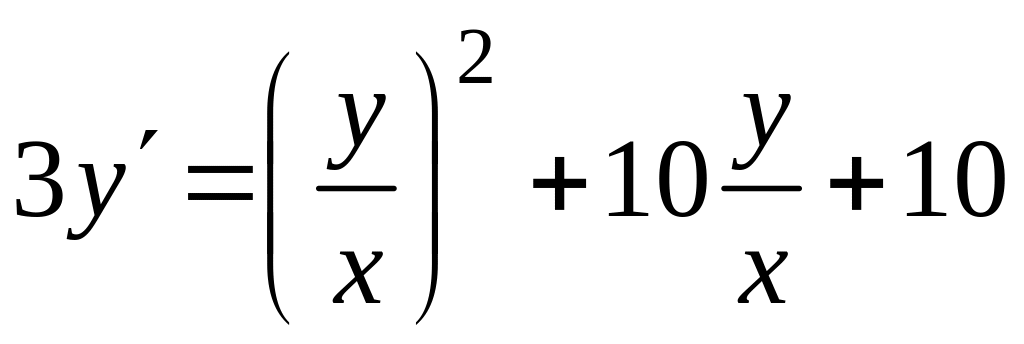 ;
;