9.2. Уравнения с разделяющимися переменными Краткие теоретические сведения

Определение. Уравнение вида:

, (2.1)

где и – некоторые функции, называется уравнением с разделенными переменными.

Это уравнение можно переписать в виде:

(2.1*)

и рассматривать как равенство двух дифференциалов.

Каждая часть уравнения с разделенными переменными представляет собой произведение некоторого выражения, зависящего от одной переменной, на дифференциал этой переменной.

Его общим интегралом будет:

, (2.2)

где С – произвольная постоянная.

Более общий случай описывают уравнением с разделяющимися переменными, которые имеют вид:

. (2.3)

ДУ (2.3) можно переписать в другой форме:

. (2.4)

Особенность ДУ (2.3) в том, что коэффициенты при и представляют собой произведения двух функций, одна из которых зависит только от , другая – только от .

Уравнением с разделяющимися переменными является любое ДУ, которое с помощью алгебраических преобразований может быть приведено к виду (2.3) или (2.4).

ДУ вида (2.3) легко сводится к уравнению (2.1) почленным делением его на .

После деления получаем:

.

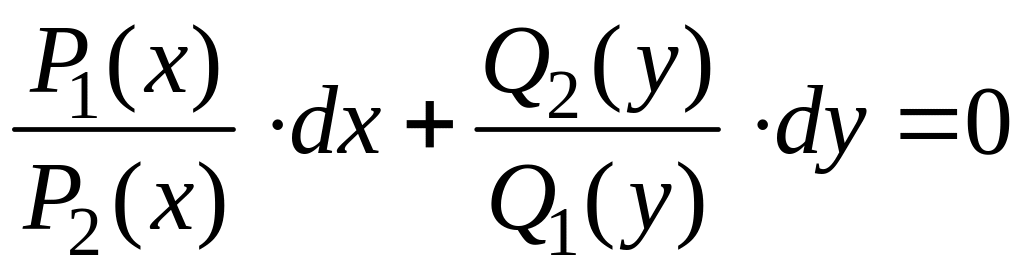Последнее равенство интегрируется согласно формуле (2.2):

.

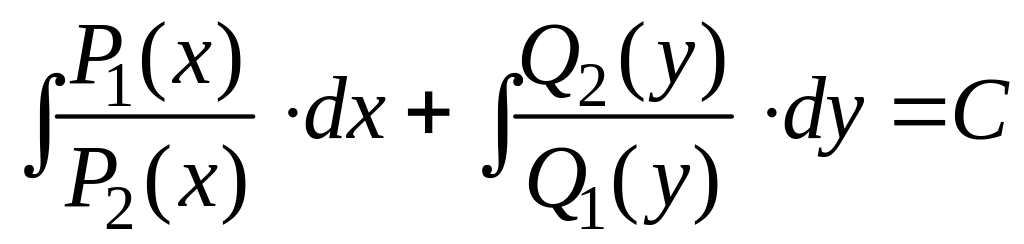Уравнение (2.4.) также сводится к уравнению с разделенными переменными, для этого достаточно обе его части умножить на и поделить на . В результате получим:

, –

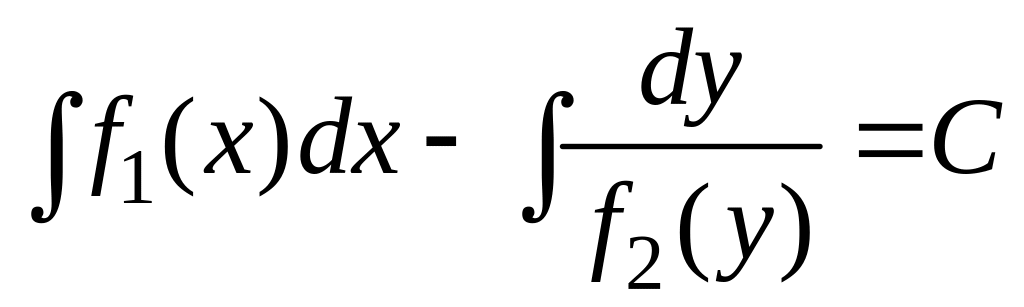общий интеграл.

Замечание. При проведении почленного деления ДУ (2.3) на , а в уравнении (2.4) – на , можно потерять те решения, которые обращают это произведение и функцию в 0. Поэтому необходимо отдельно решить уравнения и , т.е. найти те решения ДУ, которые не могут быть получены из общего решения, – особые решения.

На основании всего вышесказанного можно записать алгоритм решения ДУ с разделяющимися переменными:

• выражают производную функции через отношение ;

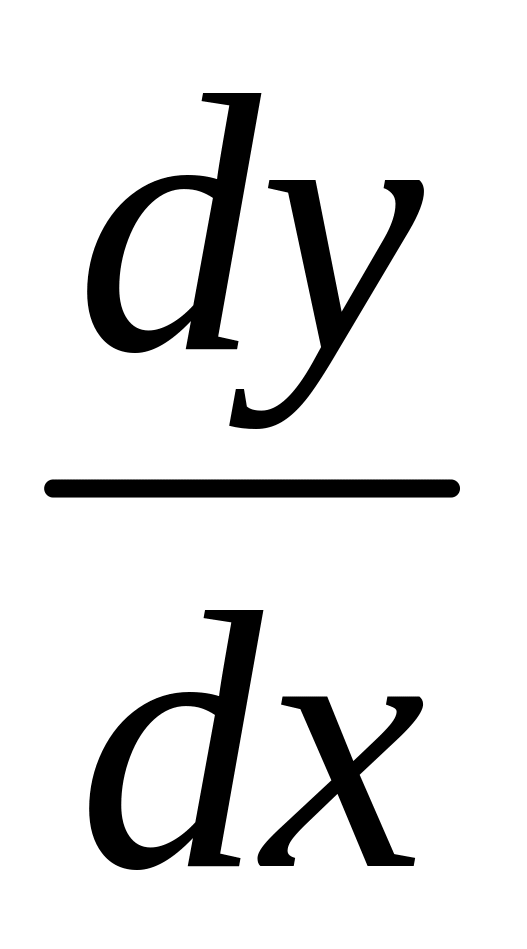• для удобства решения члены с одинаковыми дифференциалами переносят в одну сторону равенства и выносят дифференциал за скобку;

• разделяют переменные;

• интегрируют обе части равенства и находят общее решение (общий интеграл);

• находят особые решения, если они есть;

• если заданы начальные условия, то находят частное решение (частный интеграл).

В зависимости от вида ДУ некоторые пункты алгоритма решения могут быть опущены.

Примеры решения типовых задач

Пример 1. Решить ДУ с разделяющимися переменными:

.

Решение. Запишем данное уравнение в виде:

.

В каждой части равенства вынесем за скобки одинаковые множители:

.

Разделим левую и правую части уравнения на произведение . Тогда получим уравнение с разделенными переменными:

.

Интегрируя, получим:

.

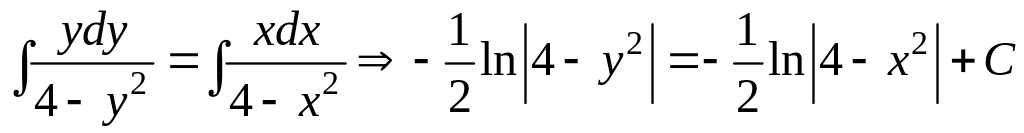Для удобства записи положим , где , тогда

Потенцируя, получим:

Освобождаемся от знака модуля:

или –

общий интеграл ДУ.

Найдем особые решения, если они имеются. Для этого решим уравнение:

.

Получаем, что . Функции ( ) удовлетворяют данному уравнению. Рассмотрим соотношение . Из него находим, что . Подставляем эти значения в уравнение, получаем тождество . Значит, также является решением данного уравнения.

Пример 2. Решить ДУ с разделяющимися переменными:

.

Решение. Учитывая, что , запишем данное уравнение в дифференциальной форме (см. формулу 1.7.):

.

Для удобства решения перепишем его в виде:

.

Разделим переменные:

,

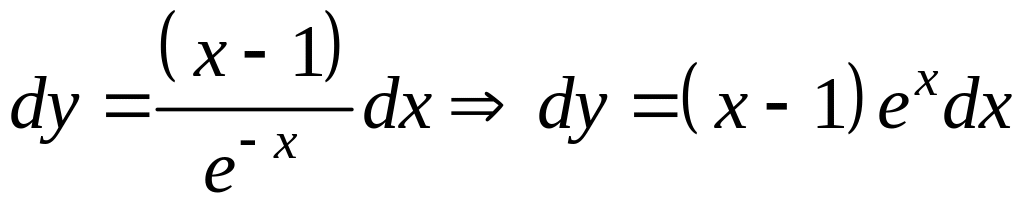тем самым мы свели уравнение к виду (2.1.*).

Проинтегрируем последнее уравнение, применяя в правом интеграле формулу интегрирования по частям:

.

Получили общее решение исходного уравнения. Так как , то особых решений нет.

Иногда для разделения переменных надо сначала сделать замену переменных.

Пример 3. Решить уравнение:

.

Решение. Сделаем замену переменных, введя новую искомую функцию , где – функция переменной , т.е. . Дифференцируя это равенство, получим:

.

Тогда уравнение примет следующий вид:

или ,

откуда

Особых решений нет, так как .

После обратной замены получаем:

–

общий интеграл.

Пример 4. Найти частное решение (интеграл) уравнения

,

удовлетворяющее начальному условию .

Решение. Применим первые два пункта алгоритма решения ДУ с разделяющимися переменными, получим:

.

Разделим левую и правую части уравнение на . Получаем уравнение с разделенными переменными:

.

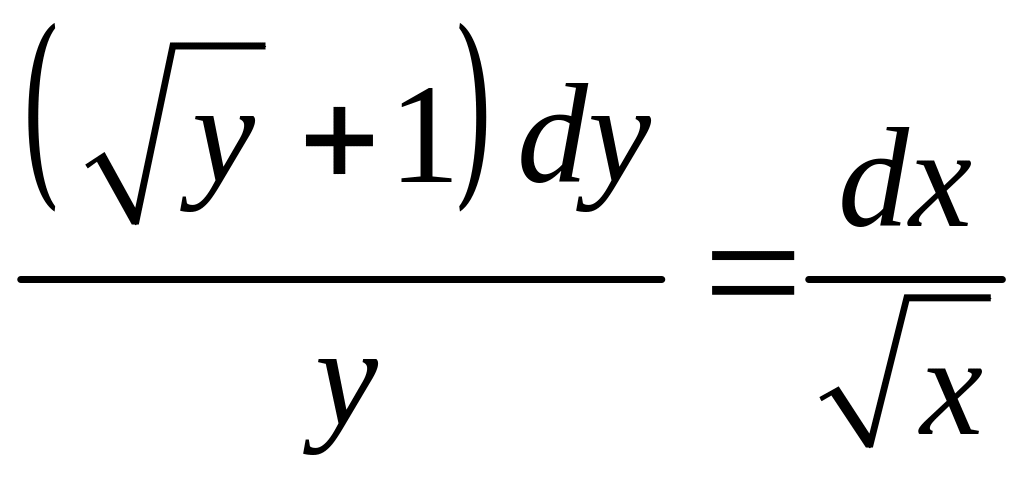Проинтегрируем последнее равенство:

.

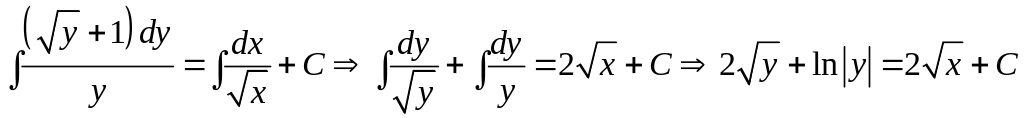Получили общий интеграл исходного ДУ.

Использовав начальное условие, определим значение произвольной постоянной, т.е. подставим в общий интеграл ДУ значения :

.

Следовательно, частное решение исходного уравнения имеет вид:

или .