§ 5. Интегралы и их приложения

5.1. Основные определения и формулы. Функция F(x) является первообразной функции f(x), если на некотором множестве X выполняется равенство F(x)=f(x). Совокупность всех первообразных для f(x) называется неопределенным интегралом и обозначается . При этом, если F(x) – какая-либо из первообразных f(x), то , константа C пробегает все множество действительных чисел. В таблице 2 на стр. 26 приводятся основные формулы, в которых u=u(x).

Таблица 2

1) 2) 3) 4) 5) 6) 7) 8) , 9)

10) 11) 12) 13) 14) 15) 16)

Очевидно, что формулы 10), 12) и 14) являются частными случаями формул 11), 13) и 15) соответственно.

Если f(x) – функция, непрерывная на отрезке [a;b], то существует определенный интеграл от этой функции, который можно вычислить по формуле Ньютона-Лейбница:

, (5.1)

где F(x) – какая-либо первообразная для f(x). В отличие от неопределенного интеграла (представляющего собой множество функций) определенный интеграл – некоторое число.

И неопределенный, и определенный интегралы обладают свойством линейности (интеграл от суммы функций равен сумме интегралов, а постоянный множитель можно выносить за знак интеграла):

,

.

Пример 5.1. Найти: а) ; б) .

Решение. В задании а) подынтегральную функцию сначала упрощаем, разделив почленно каждое слагаемое из числителя на знаменатель, затем используем свойство линейности и «табличные» формулы 1)-3):

В задании б), помимо линейности и «табличных» формул 3), 9), 1), используем формулу Ньютона-Лейбница (5.1):

5.2. Внесение под знак дифференциала и замена переменной. Можно заметить, что иногда часть подынтегральной функции образует дифференциал некоторого выражения, что позволяет применять табличные формулы.

Пример 5.2 Найти: а) ; б) .

Решение. В примере а) можно заметить, что , а затем воспользоваться формулой 5) при u=lnx:

В случае б) , а потому в силу 11) при получим:

Замечание 1. При внесении под знак дифференциала полезно, наряду с использованными выше, учитывать следующие соотношения:

; ; ; ; ;

; ; ; .

Замечание 2. Интегралы из примера 5.2. можно было найти и с помощью замены переменной. При этом в определенном интеграле следует менять и пределы интегрирования. Преобразования в 5.2.б) выглядели бы, например, так:

В общем случае выбор замены определяется видом подынтегральной функции. В некоторых случаях рекомендуются специальные замены. Например, если в выражении присутствует иррациональность вида , то можно положить или .

Пример 5.3 Найти: а) ; б) .

Решение. В случае а) имеем

(после замены применили табличную формулу 11)).

При решении б) обязательно проводим замену пределов интегрирования.

5.3. Интегрирование по частям. В ряде случаев помогает «формула интегрирования по частям». Для неопределенного интеграла она имеет вид

, (5.2)

для определенного

, (5.3)

При этом важно учитывать следующее.

1) Если подынтегральная функция содержит произведение многочлена от x на функции , то в качестве u выбирается многочлен, а оставшееся под знаком интеграла выражение относится к dv.

2) Если подынтегральная функция содержит обратные тригонометрические ( ) или логарифмические ( ) функции, то в качестве u выбирается одна из них.

Пример 5.4. Найти: а) ; б) .

Решение. В случае а) применяем формулу (5.2) и второе правило. Именно, полагаем . Тогда . Далее, , а потому . Следовательно, . В полученном интеграле выделим целую часть подынтегральной функции (так поступают, когда степень числителя не меньше степени знаменателя):

.

Окончательно решение выглядит так:

В примере б) используем (5.3) и первое из правил.

5.4. Интегрирование выражений, содержащих квадратный трехчлен. Основные идеи заключаются в выделении в квадратном трехчлене полного квадрата и в проведении линейной замены, позволяющей свести исходный интеграл к табличным вида 10)-16).

Пример 5.5. Найти: а) ; б) ; в) .

Решение. В случае а) действуем следующим образом:

,

поэтому (с учетом 13) )

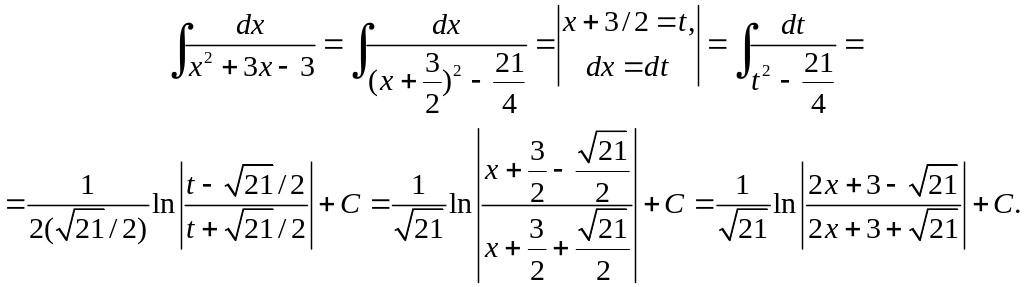
При решении примера б) потребуются дополнительные преобразования, связанные с присутствием переменной в числителе подынтегральной функции. Выделив полный квадрат в знаменателе ( ), получим:

Для второго из интегралов в силу 11) (табл.2) имеем: . В первом интеграле проведем внесение под знак дифференциала:

.

Таким образом, собирая все вместе и возвращаясь к переменной x, получаем:

В примере в) также предварительно выделяем полный квадрат:

.

Далее проводим замену переменной ( ) и окончательно имеем:

5.5. Интегрирование простейших тригонометрических функций. При интегрировании выражений вида (где m и n – натуральные числа) рекомендуется принимать во внимание следующие правила.

1) Если обе степени четные, то применяются формулы «понижения степени»: ; .

2) Предположим, что какое-либо из чисел m и n – нечетное. Например, n=2k+1. В этом случае одну из степеней функции cosx «отщепляют», чтобы внести под знак дифференциала (т.к. ). В оставшемся выражении с помощью основного тригонометрического тождества выражают через ( ). После преобразования подынтегрального выражения (и с учетом свойства линейности) получается алгебраическая сумма интегралов вида , каждый из которых можно найти с помощью формулы 2) из таблицы 2: .

Кроме того, в некоторых случаях полезны также формулы

; (5.4)

; (5.5)

. (5.6)

Пример 5.6. Найти: а) ; б) ; в) .

Решение. а) В подынтегральную функцию входит нечетная (5-я) степень sinx, поэтому действуем по второму правилу, учитывая, что .

В примере б) воспользуемся формулой (5.4), линейностью неопределенного интеграла, равенством и табличной формулой 4):

В случае в) последовательно понижаем степень, учитываем линейность, возможность внесения константы под знак дифференциала и нужные табличные формулы:

5.6. Приложения определенного интеграла. Как известно, криволинейной трапецией, соответствующей неотрицательной и непрерывной на отрезке [a;b] функции f(x), называется область, ограниченная графиком функции y=f(x), осью OX и двумя вертикальными прямыми x=a, x=b. Коротко это можно записать так: (см. рис.3).

Геометрический смысл определенного интеграла заключается в том, что площадь такой криволинейной трапеции вычисляется по формуле

(5.7)

Если область на плоскости имеет вид (см. рис.4), причем от обеих функций требуется только непрерывность, то справедлива формула

. (5.8)

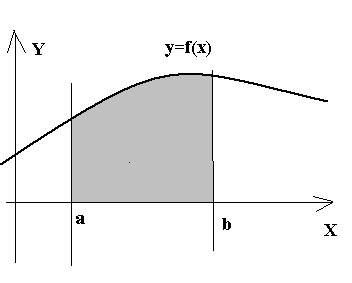
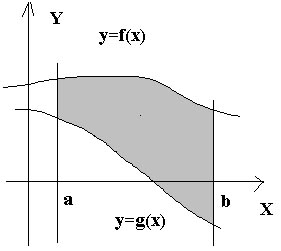
Рис. 3 Рис. 4

Пример 5.7. Найти площадь области, ограниченной:

а) осью ОХ и линиями ;

б) графиками функций .

Решение. Предварительно необходимо построить соответствующие графики и определить область, площадь которой нужно найти. Для случая а) это сделано на рис.5 (стр.35). Очевидно, что заштрихованная область представляется в виде объединения двух криволинейных трапеций: и . Здесь – абсцисса точки пересечения графиков функций . Нужное значение найдем, решая соответствующую систему уравнений:

Таким образом, выбираем решение (с учетом того, что ). Площади криволинейных трапеций и находим по формуле (5.7), а затем суммируем, чтобы получить область всей интересующей нас области:

.

В случае б) графики и область, площадь которой надо найти, изображены на рис.6 (стр.35). Очевидно, что мы имеем дело с объединением двух областей. При этом (эта криволинейная трапеция состоит из двух симметричных относительно оси OX частей, поэтому , где ) и . Как и выше, и - абсциссы точек пересечения графиков, которые находим, решая систему уравнений:

откуда и . Для вычисления площади криволинейной трапеции применяем формулу (5.7), для вычисления площади - (5.8):

Окончательно имеем:

Замечание. Другие примеры, связанные с нахождением неопределенных и определенных интегралов и определением площадей плоских областей можно найти в [1, стр.19-24], [2, стр.3-8] и [4, стр.3-11].

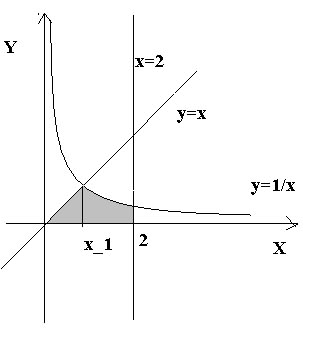
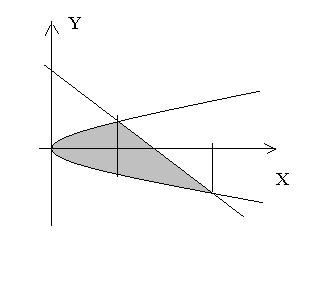
Рис. 5 Рис.6