§ 2. Классификация точек разрыва

При решении задач используются следующие определения.

Точка x=a называется точкой устранимого разрыва функции y=f(x), если выполняется одно из условий: 1) a не принадлежит области определения данной функции, но существует конечный ; 2) a принадлежит области определения данной функции, существует конечный , но .

Точка x=a называется точкой разрыва первого рода функции y=f(x), если не существует, но существуют конечные, различные между собой односторонние пределы и

Точка x=a называется точкой разрыва второго рода функции y=f(x), если хотя бы один из односторонних пределов , равен бесконечности или не существует.

При определении характера разрыва в точке x=a необходимо сначала найти . Если этот предел существует, то x=a окажется (в зависимости от значения предела) либо точкой устранимого разрыва, либо точкой разрыва второго рода. Если не существует, то находят односторонние пределы – в зависимости от них x=a будет точкой разрыва первого или второго рода.

Пример 2.1. Найти и классифицировать точки разрыва функции .

Решение. 1) Выражения, стоящие в числителе и знаменателе, непрерывны при всех вещественных x. Однако знаменатель обращается в нуль при x=0 и x=-1, т.е. эти точки не принадлежат области определения и являются точками разрыва. Исследуем каждую из них.

2) Рассмотрим x=0. Так как , а рассматриваемая точка не принадлежит области определения, заключаем, что x=0 – точка устранимого разрыва.

3) Пусть теперь x=-1. Так как при , а , то заключаем, что . Следовательно, x=-1 – точка разрыва второго рода.

Замечание. Другие примеры, связанные с определением характера разрыва, можно найти в [1, стр.10-11].

§ 3. Дифференцирование функций

3.1. Правила дифференцирования функций одного переменного. При нахождении производных и дифференциалов функции применяются следующие правила:

; (3.1)

; (3.2)

; (3.3)

. (3.4)

Заметим, что (3.3) следует из (3.2), так как производная константы всегда равна нулю ( ).

Чтобы найти производную функции в точке , необходимо сначала найти , а затем в полученное выражение подставить заданное значение.

Необходимо также знать таблицу производных основных элементарных функций. В Таблице 1 формулы приводятся как для функции независимого аргумента , так и для сложной функции .

Таблица 1

1) , 2) 3) 4) 5) 6) , 7) 8) , 9) 10) 11) 12) 13)

1) 2) 3) 4) 5) 6) , 7) 8) , 9) 10) 11) 12) 13)

Дифференциал функции в произвольной точке задается формулой

, (3.5)

а в фиксированной точке формулой

. (3.6)

Для определения производной второго порядка используем правило

. (3.7)

Пример 3.1. Найти производную для и выписать дифференциал этой функции.

Решение. Данную функцию можно представить в виде , где , и воспользоваться формулой 9) из Табл.1. Далее к числителю полученного выражения применяем (3.1), а функцию также рассматриваем как сложную и находим ее производную с помощью 4):

Итак, , а (в силу (3.5)).

Пример 3.2. Найти производную функции в точке x=2.

Решение. Функция представляет собой частное, поэтому применяем (3.4), а также формулу производной степенной функции (для и для ):

Вычисляем производную в заданной точке, для этого подставляем в найденное выражение значение x=2:

.

Пример 3.3. Найти дифференциал функции в произвольной точке и в точке x=/2.

Решение. Сначала найдем первую производную исходной функции, воспользовавшись формулами 7), (3.4) и 2):

Далее вычисляем производную в точке x=/2. Поскольку и , то . В силу (3.6) .

Пример 3.4. Найти вторую производную функции .

Решение. Сначала найдем и обязательно упростим полученное выражение:

Теперь в силу (3.7) и 1) получаем:

.

3.2. Правило Лопиталя вычисления пределов. Если при вычислении пределов затруднительно использование эквивалентностей, то можно применить следующее утверждение.

Правило Лопиталя. Пусть функции f(x) и g(x) определены и дифференцируемы в окрестности точки a, а также являются одновременно бесконечно малыми (или бесконечно большими) при . Пусть, далее, в окрестности точки a (кроме, возможно, самой точки). Если существует , то существует и , причем .

Пример 3.5. Найти с помощью правила Лопиталя:

а) ; б)

Решение. a) В данном случае после подстановки x=0 замечаем, что и числитель, и знаменатель дроби обращаются в нуль, т.е. мы имеем дело с неопределенностью . Однако использовать замечательные пределы и перейти к эквивалентным функциям нельзя, так как в числителе – сумма. Воспользуемся правилом Лопиталя, предварительно проверив все условия.

Неопределенность уже отмечена. Функции, стоящие в числителе и знаменателе, дифференцируемы при всех вещественных x и при . В силу сформулированного выше утверждения, если в этом случае существует предел отношения производных, то его значение совпадет со значением искомого предела. Предположим, что это так, и проведем вычисления:

Итак,

При решении этого примера правило Лопиталя фактически было применено трижды (в тех местах, где над знаком равенства указан вид неопределенности). При этом для обеспечения строгости рассуждений необходимо каждый раз проверять условия сформулированного выше утверждения.

Рассмотрим теперь задание б). Очевидно, что здесь вообще нет эквивалнетных функций. Кроме того, при и . Это неопределенность вида , к которой правило Лопиталя не применяется, однако можно учесть, что если f(x) – бесконечно малая при функция, то 1/f(x) будет бесконечно большой при . Поскольку

,

то мы приходим к неопределенности и далее действуем так, как при решении задания а). Обе функции требуемым условиям удовлетворяют, поэтому

(учтено, что ). Итак, .

3.3. Правила дифференцирования функций двух переменных. При дифференцировании функции по одной из независимых переменных вторая фиксируется и считается константой (это следует из определения частных производных первого порядка). Применяются уже знакомые правила (.3.1)-(3.4) и формулы из табл.1, однако при записи обязательно указывается, по какой переменной происходит дифференцирование. Так, для производной по x используются обозначения или . Аналогично запись обозначает производную по y.

Для полного дифференциала первого порядка функции имеем:

; (3.8)

. (3.9)

Частные производные второго порядка определяются по формулам

; ; (3.10)

; . (3.11)

Заметим, что если исходная функция удовлетворяет некоторым дополнительным свойствам, то справедливо равенство В этом случае говорят, что «смешанные производные второго порядка» совпадают, или «смешанная производная не зависит от порядка дифференцирования».

Справедлива формула для полного дифференциала второго порядка функции :

(3.12)

Пример 3.6. Найти частные производные первого порядка и выписать дифференциал первого порядка функции

Решение. Чтобы найти , необходимо зафиксировать переменную y. Воспользовавшись формулой 3) из Табл.1, а также (3.1) и (3.3), получим:

В данном случае числовой коэффициент и переменная y выступали в роли констант: во втором слагаемом они были вынесены за скобки при дифференцировании, а третье слагаемое от x не зависело – поэтому его производная по x равна нулю.

Аналогично поступаем и с , только теперь фиксируется переменная y:

Чтобы выписать дифференциал первого порядка, воспользуемся (3.8.):

Пример 3.7. Найти частные производные второго порядка функции . Выписать .

Решение. Сначала находим частные производные первого порядка. Следует обратить внимание на то, что при фиксированном y функция представляет собой произведение двух функций, зависящих от x, а при фиксированном x это константа, умноженная на функцию от y. Применяя известные уже приемы дифференцирования, получаем:

.

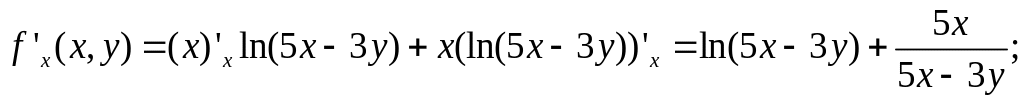
Теперь воспользуемся формулами (3.10) и любой из формул (3.11).

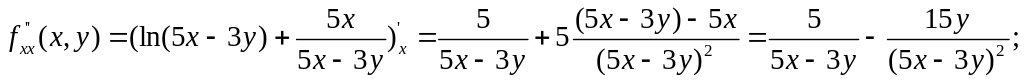
В качестве проверки можно найти вторую смешанную производную и убедиться, что результаты совпадают:

Чтобы записать теперь дифференциал второго порядка в заданной точке (1;1), вычислим значения производных в этой точке, а затем применим (3.12):

; ; ;

.

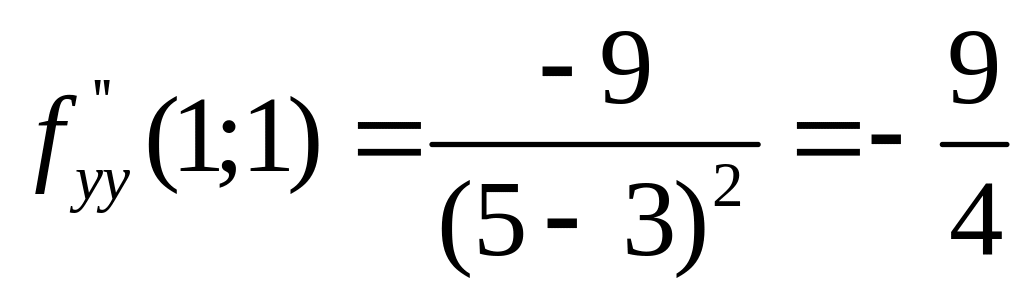3.4. Производная по направлению и градиент. Пусть — функция двух переменных, определенная в некоторой области D, M(x,y) – произвольная точка этой области, – некоторое направление (вектор, соединяющий

Рис.1

начало координат с точкой (a,b) и передвинутый параллельным переносом из начала координат в точку M). Через  и  обозначим углы, образованные вектором направления с положительными направлениями осей OX и OY. Так как (см. рис. 1) , то справедливы формулы , . (3.13) При этом и называются «направляющими косинусами».:

Производная функции по направлению в точке M задает скорость изменения функции в этом направлении и может быть найдена по формуле

. (3.14)

Градиентом функции в точке M называют вектор с координатами, равными значениям частных производных первого порядка в этой точке:

. (3.15)

Он определяет направление наискорейшего возрастания функции, а его величина, которую находят по формуле

, (3.16)

совпадает с максимальной скоростью возрастания функции в данной точке.

Пример 3.7. Пусть . Найти градиент функции в точке M(3;1), величину градиента функции в этой точке и производную функции в той же точке по направлению .

Решение. Предварительно находим частные производные функции первого порядка и их значения в заданной точке:

Теперь воспользуемся формулами (3.15) и (3.16):

; .

Далее, , поэтому в силу (3.13) , , и в силу (3.14):

.

Замечание. Решение других задач, связанных с дифференцированием, можно найти в [1, стр.12-14], [2, стр.18-22], [3, стр.22-27], [4, стр.14-16].