37

ВВедение

В данном методическом пособии приводятся подробные решения основных типовых задач и упражнений по всем разделам математического анализа, которые изучаются в общем курсе «Высшая математика». Студентам-заочникам рекомендуется тщательно разобрать все примеры и придерживаться предложенных алгоритмов при выполнении заданий первой индивидуальной домашней контрольной работы из [10]. Студенты дневного отделения могут использовать данные указания при решении домашних упражнений в течение семестра, а также при подготовке к контрольным работам и экзамену.

Дополнительную информацию теоретического характера можно найти в учебниках [5]–[7] (по всем разделам), а также в [9] (для §§1–2, пп. 3.1, 3.2, 4.1–4.4, 5.1–5.5). Решения задач, не вошедших в данное пособие, имеются в [1] –[4] и в [8].

§ 1. Вычисление пределов

1.1. Основные теоретические положения. Вычисление пределов опирается на свойства бесконечно малых и бесконечно больших функций и основные теоремы об арифметических действиях с пределами. Используется также один из известных замечательных пределов:

(1.1.)

Следует учитывать и теорему о пределе сложной функции. В частности, в силу этого утверждения

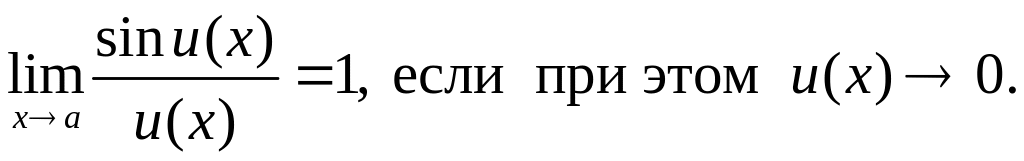(1.2)

Пусть , . При вычислении предела алгебраической суммы функций возможны ситуации:

1) если A и B – конечные числа, тогда (по теореме о пределе алгебраической суммы);

2) если один из пределов (A или B) конечен, а другой является одним из бесконечных символов, то (в силу свойств бесконечно больших функций);

3) в случае, когда f(x) и g(x) – бесконечно большие функции одного знака, то ; если же f(x) и g(x) – бесконечно большие функции разных знаков, то ничего конкретного (в общей ситуации) утверждать нельзя, поэтому говорят о неопределенности вида , требующей дополнительного исследования.

Вычисляя предел произведения функций, необходимо учитывать следующее:

1) если A и B – конечные числа, то (по теореме о пределе произведения);

2) если один из пределов (A или B) конечен и отличен от нуля(!), а другой является одним из бесконечных символов, то (по свойству бесконечно больших функций);

3) если один из пределов равен нулю, а второй является одним из бесконечных символов, то говорят о неопределенности вида .

Наконец, при вычислении пределов частного применяются такие правила:

1) если A и B – конечные числа, причем B0, то 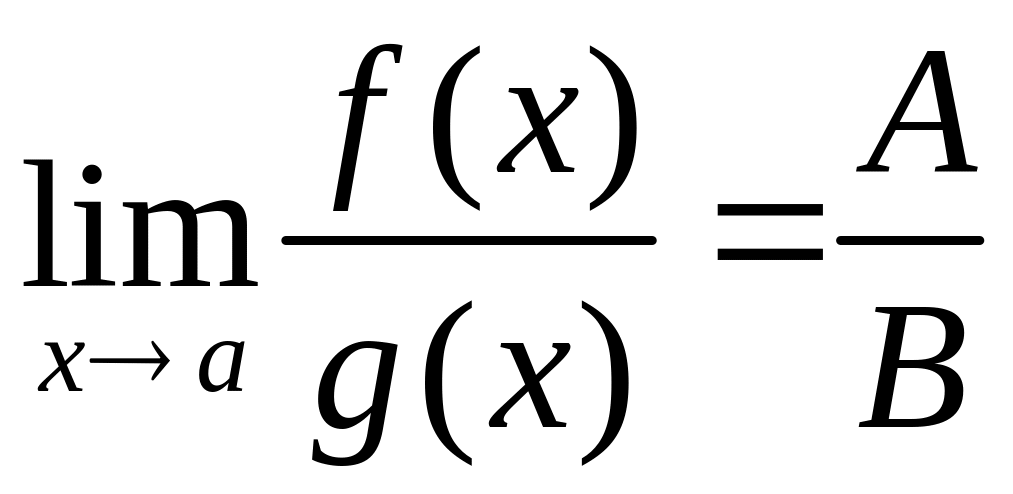(по теореме о пределе частного);

2) если A и B – конечные числа, причем A0, B=0, то (так как функция 1/g(x) при этом является бесконечно большой при и остается воспользоваться свойствами бесконечно больших функций);

3) если , а B – любое конечное число, то , а если , а А – любое конечное число, то 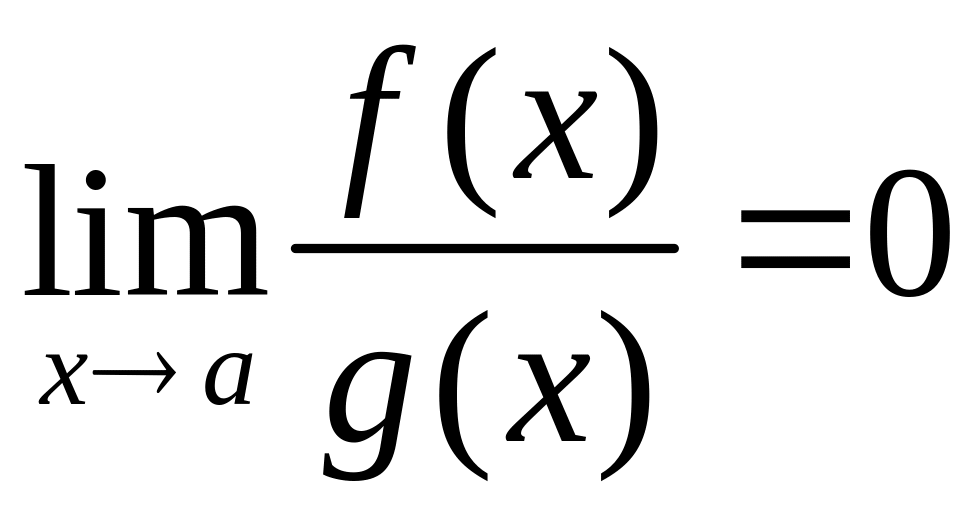(в силу свойств бесконечно больших функций);

4) наконец, если A=B=0, то говорят о неопределенности вида , а если A и B – бесконечные символы, то о неопределенности вида .

1.2. Раскрытие неопределенностей вида . В данном случае в числителе и знаменателе рекомендуется вынести за скобки слагаемое, которое растет быстрее других (для многочленов, в частности, это слагаемое, имеющее старшую степень). В результате алгебраическая сумма представляется в виде произведения бесконечно большой функции на функцию, имеющую конечный и отличный от нуля предел.

Пример 1.1. Вычислить .

Решение. Предел последовательности можно рассматривать как частный случай предела функции. Очевидно, что в силу свойств бесконечно больших функций при и . Поэтому имеем неопределенность вида . Проведем подготовительные преобразования:

; .

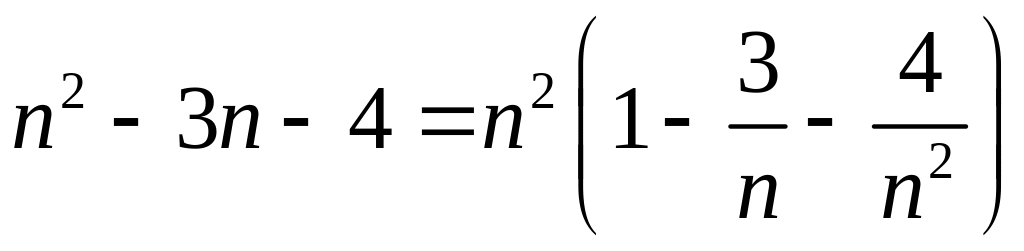Далее получаем:

.

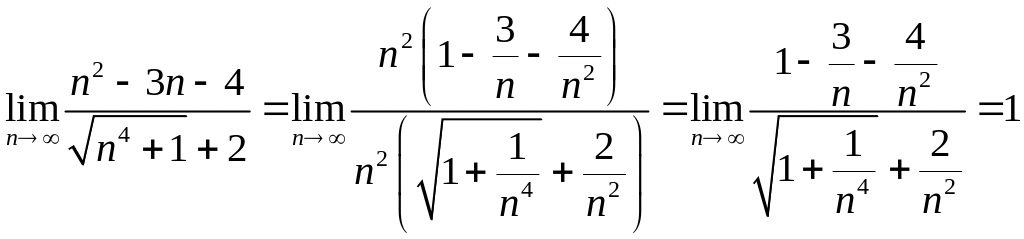Последнее равенство справедливо в силу теорем о пределе суммы и частного функций с учетом того, что все слагаемые, кроме единиц, являются бесконечно малыми (по теореме о связи между бесконечно большой и бесконечно малой функциями).

1.3. Раскрытие неопределенностей вида . Неопределенности такого вида возникают, как правило, либо при исследовании разности двух дробей (в этом случае рекомендуется приводить дроби к общему знаменателю), либо при рассмотрении разности иррациональных выражений (для избавления от иррациональностей следует преобразовать исходное выражение либо к разности квадратов, либо к сумме или разности кубов). Далее задача сводится к рассмотренной выше неопределенности вида .

Пример 1.2. Вычислить .

Решение. В данном случае, чтобы раскрыть неопределенность , необходимо умножить и разделить рассматриваемое выражение на «сопряженное», чтобы прийти к разности квадратов. Для таким «сопряженным» является . Таким образом, получаем:

.

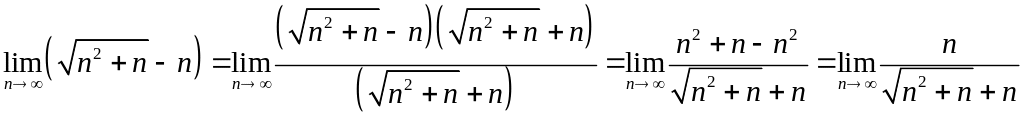Таким образом, мы попали в ситуацию, разобранную при решении примера 1.1. Проведем соответствующие преобразования в знаменателе:

.

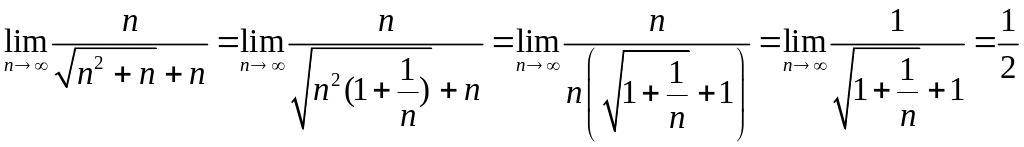Итак, .

1.4. Раскрытие неопределенностей вида . В этой ситуации основная цель преобразований – выделить в числителе и знаменателе множители вида (x-a) (именно они при вычислении предела при "обеспечивают" наличие неопределенности).

Пример 1.3. Вычислить .

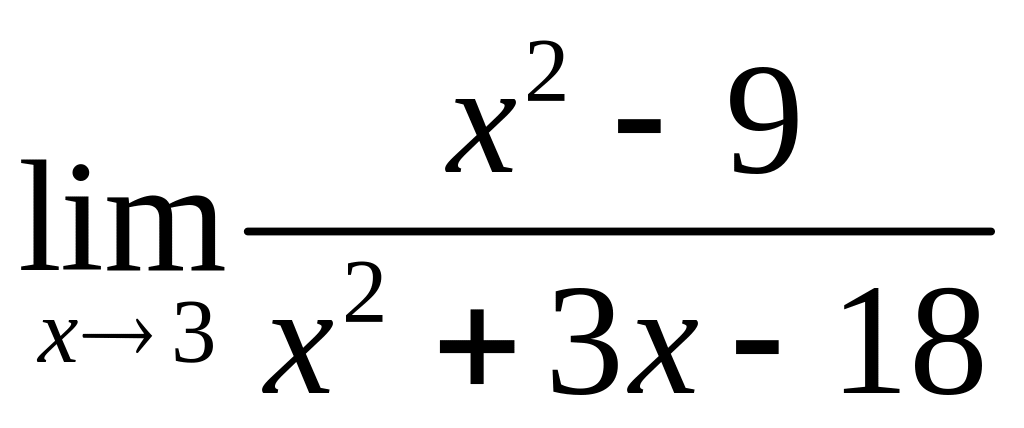Решение. Подставляя предельное значение x=3 в числитель и знаменатель, получаем, что оба выражения обращаются при этом в нуль. Стоящие в числителе и знаменателе многочлены можно разложить на множители, причем в числителе достаточно воспользоваться формулой разности квадратов, а в знаменателе необходимо предварительно найти корни соответствующего квадратного трехчлена. Следует помнить, что если – корни квадратного трехчлена , то справедлива формула

, (1.3)

а для трехчлена выполняется равенство

. (1.4)

Таким образом, имеем:

.

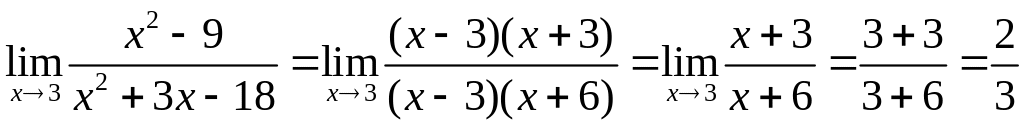Пример 1.4. Вычислить

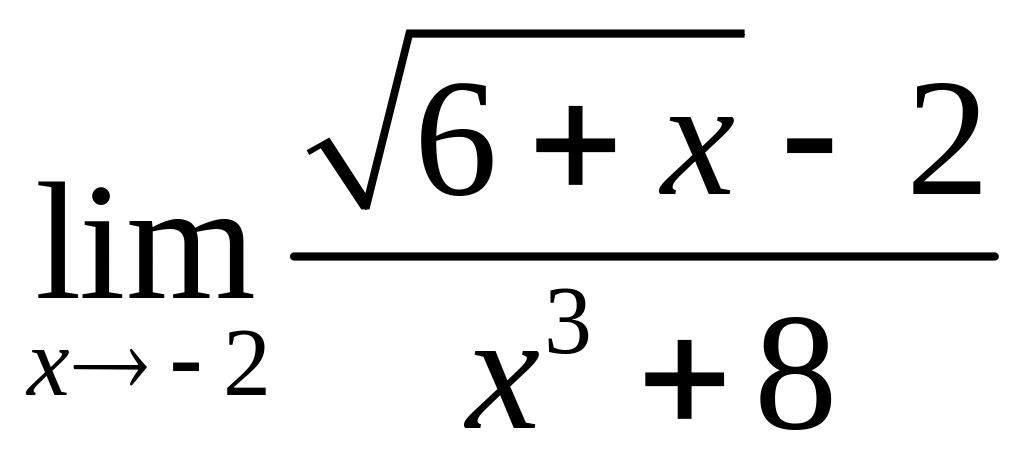
Решение. Подставляя предельное значение x=2 в числитель и знаменатель, получаем, что оба выражения обращаются в нуль. Знаменатель представляет собой «сумму кубов», поэтому при разложении его на множители получаем: . После умножения числителя и знаменателя на сопряженное числителю выражение , имеем:

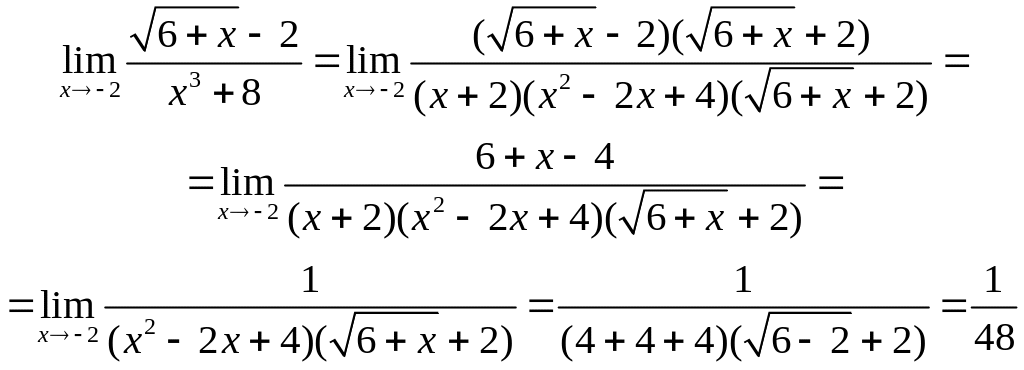
При вычислении пределов тригонометрических функций применяются «замечательные пределы» (1.1) и (1.2).

Пример 1.5. Вычислить а) ; б) ; в) .

Решение. В случае а) очевидно, что при и . Чтобы применить (1.2), необходимо получить в знаменателе выражение, совпадающие с аргументом синуса. Для этого числитель и знаменатель умножаем на число «4»:

.

Однако на практике оказывается полезной теорема, согласно которой в произведении и в частном эквивалентные функции (т.е. те, для которых выполняется равенство 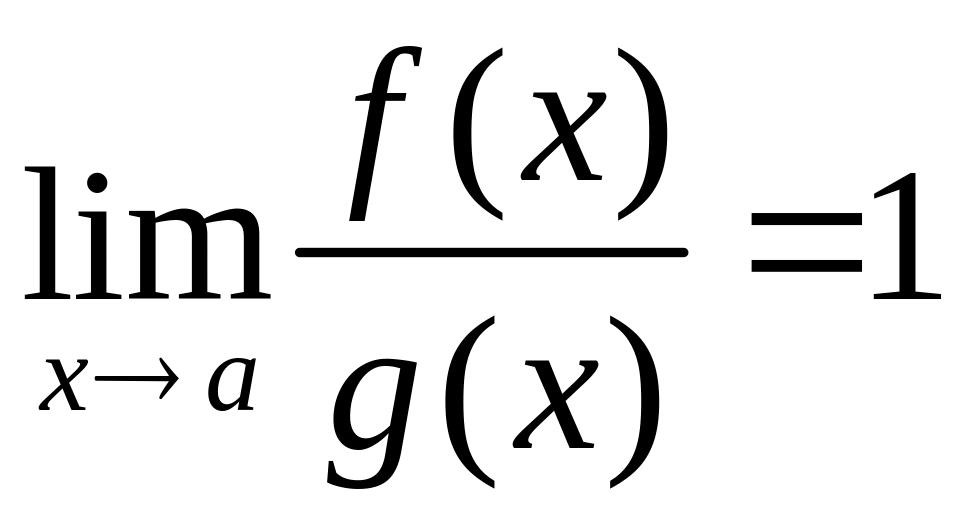) можно заменять друг другом. В частности,

; . (1.5)

Поэтому решение а) можно записать в следующем виде: .

В случае б) знаменатель разложим на множители как «разность квадратов», а в числителе воспользуемся одним из соотношений (1.5):

.

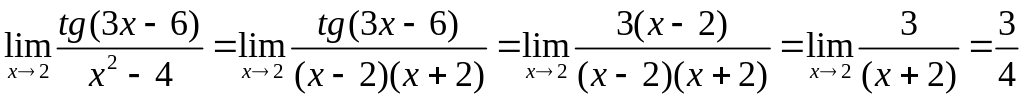В задании в) необходимо сначала преобразовать числитель в произведение, используя формулу разности синусов, а потом применить эквивалентные соотношения из (1.5), учитывая, что :

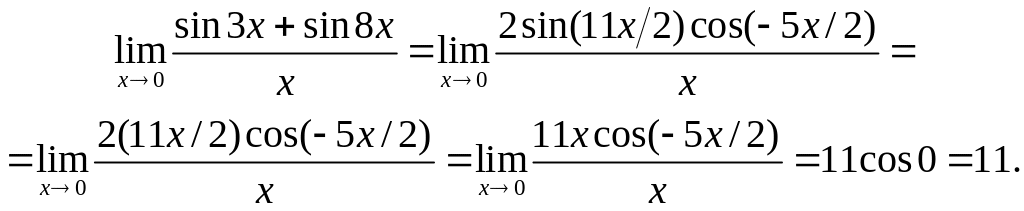
Замечание. Другие примеры на вычисление пределов можно найти в [1, стр.6-9] и в [3, стр.7-18].