§ 2. Абсолютна збіжність невласних інтегралів. Алгебраїчні властивості

Нехай функція інтегруєма за Ріманом на будь-якому відрізку , де може бути як скінченним, так і нескінченним. Нагадаємо, що запис означає, що функція необмежена в точці (невласний інтеграл другого роду), або (невласний інтеграл першого роду).

Згідно з властивістю визначеного інтеграла

.

Звідки і одержимо достатню умову : якщо збігається, то і збігається (безумовно, за умови, що на будь-якому функція інтегруєма).

Так, наприклад, буде збіжним інтеграл за умови, що збігається (нагадаємо, що ).

Означення 2.1. Якщо збігається, то кажуть, що абсолютно збігається.

Таким чином,

1) коли кажуть, що абсолютно збігається, то тут міститься і твердження, що сам інтеграл також збігається;

2) якщо на функція , то збіжність одночасно буде і абсолютною збіжністю;

3) якщо , то функція 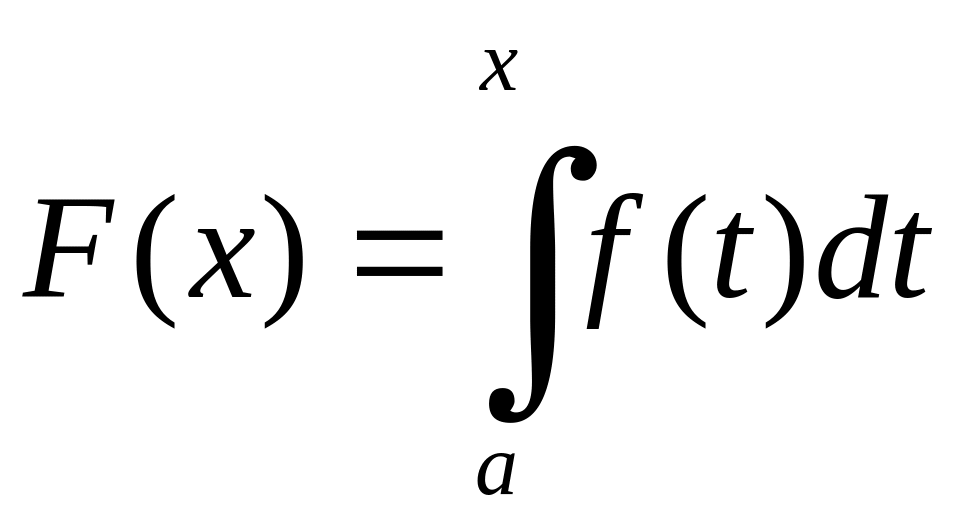зростає разом із . Тоді для того, щоб існував , необхідно і достатньо, щоб інтеграли були обмеженими зверху.

Цей результат є аналогом критерію збіжності монотонно зростаючої обмеженої послідовності.

4) інтеграл може збігатись, але не абсолютно, тобто при цьому розбігається, . Приклад такої функції ми приведемо пізніше, в теорії рядів. Такий інтеграл називають умовно збіжним.

Компактним інтервалом (відрізком) на називають обмежений замкнутий інтервал .

Алгебраїчні властивості інтегралів на (кажуть “на некомпактному проміжку ”) зрозумілі, але необхідно попередньо упевнитись, що функції визначені на одному і тому ж проміжку і що інтеграли від них збігаються. А тому:

1. Якщо існує, то .

2. Якщо і існують, то

Таким чином, множина функцій , інтегруємих на некомпактному проміжку і таких, що збігаються, є лінійним простором і відображення є лінійна форма.

§ 3. Заміна змінної в невласному інтегралі

Нехай функція визначена на некомпактному проміжку і неперервна. Нехай є така первісна для неперервної функції на інтервалі , що ( - скінчені числа). Тоді, як відомо, для будь-якого

Припустимо, що існує, і що має границю , коли прямує до . Тоді

.

Отже, за вказаними умовами в інтегралі на некомпактному проміжку можна виконувати заміну змінної, тобто можна знайти функцію з неперервною першою похідною, яка виконує взаємно однозначне і взаємно неперервне відображення між та таке, що , . Тоді і

.

Зокрема, якщо збігається абсолютно і така неперервна строго зростаюча функція з неперервною (і невід’ємною) першою похідною , що , то

,

Абсолютна збіжність при вказаній заміні зберігається.

Приведемо два наслідка:

а) нехай неперервна функція на компактному інтервалі . Тоді

.

При цьому функція неперервна на , але не обов’язково на , ( - скінчені, , ).

Приклад 3.1. Нехай на і нехай , , .

Маємо

.

Таким чином, у результаті вибраної заміни інтеграл від обмеженої функції на переходить в інтеграл від необмеженої функції на .

б) припустимо, що - скінчені, - скінчене, , неперервна на , , . Тоді

.

Приклад 3.2.

Приклад 3.3. Нехай

.

Тоді

.

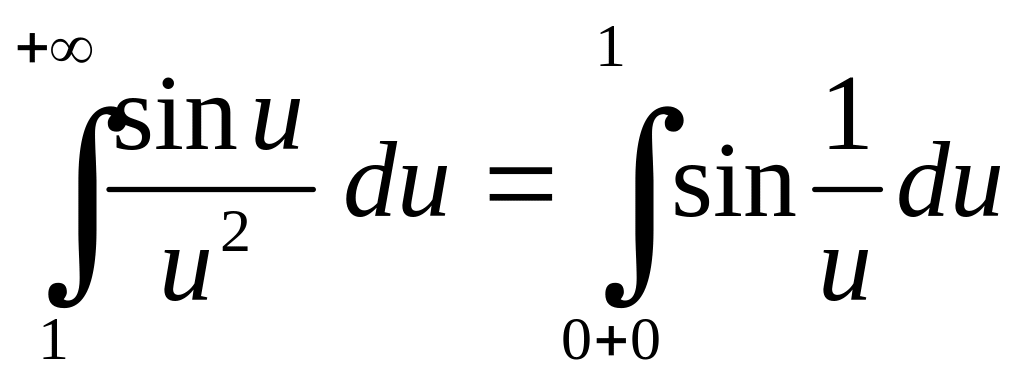Приклад 3.4. Нехай

.

Тоді

.