Розділ IV. Невласні інтеграли

При означенні визначеного інтеграла Рімана передбачається, що відрізок інтегрування скінчений, а функція визначена на цьому проміжку та обмежена. При розгляданні прикладів ми зустрілись із двома випадками, коли в результаті заміни підінтегральна функція на проміжку інтегрування стала необмеженою, а також у результаті заміни скінчений проміжок відобразився в нескінченний. Можна привести багато прикладів такого типу, а тому виникла потреба розширити поняття інтеграла Рімана. Якщо проміжок інтегрування нескінченний, то такі інтеграли називають невласними інтегралами Рімана першого роду, або невласними інтегралами на нескінченному проміжку. При цьому припускається, що функція інтегрована на будь-якому скінченому проміжку, який є частиною нескінченого.

Якщо проміжок інтегрування скінчений, а функція необмежена на ньому, то такі інтеграли називають невласними інтегралами Рімана другого роду, або невласними інтегралами на скінченому проміжку.

§ 1. Означення невласних інтегралів Рімана, приклади

Означення 1. Нехай функція визначена на проміжку і інтегруєма на будь-якому відрізку , де .

Символ 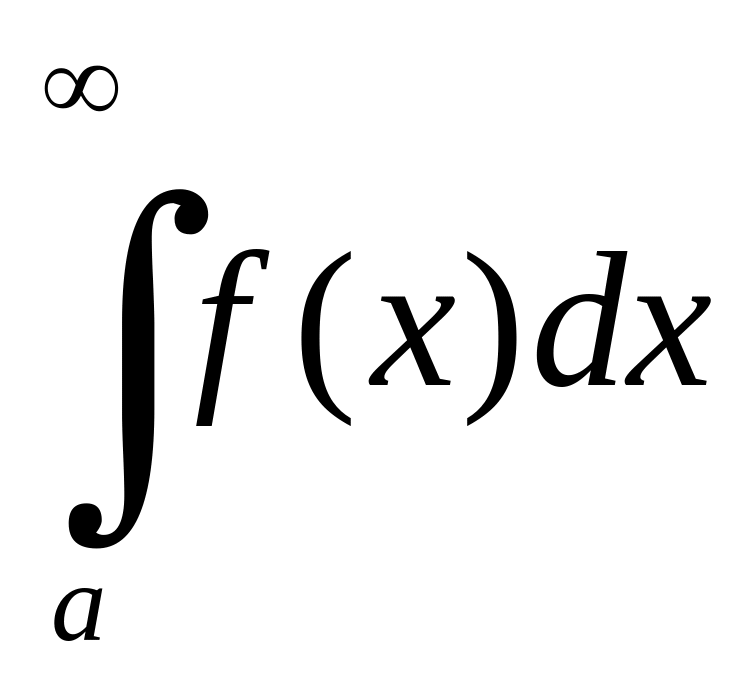називають невласним інтегралом на нескінченному проміжку (або невласним інтегралом першого роду), його розуміють як границю:

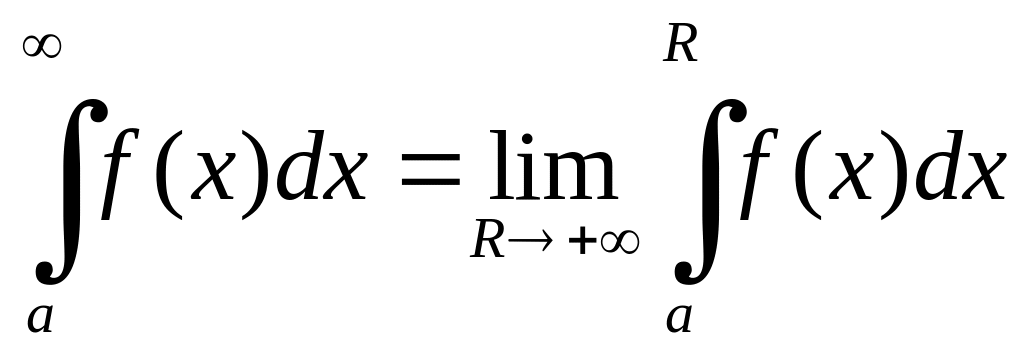
і кажуть, що невласний інтеграл збігається, якщо існує скінчена границя (1.1) і його величина дорівнює цій границі. Якщо границя не існує, зокрема, дорівнює , то кажуть, що невласний інтеграл є розбіжним (інтеграл розбігається).

Таким чином, невласний інтеграл буде визначеним, якщо існує скінчена границя (1.1).

Приклад 1.1. Дослідити, при яких значеннях параметра збігається (або буде визначений ) невласний інтеграл

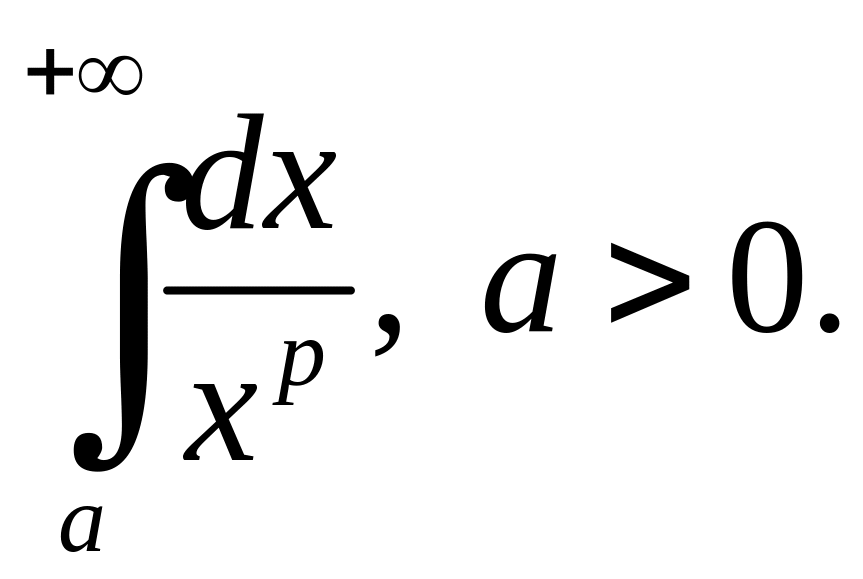
Оскільки

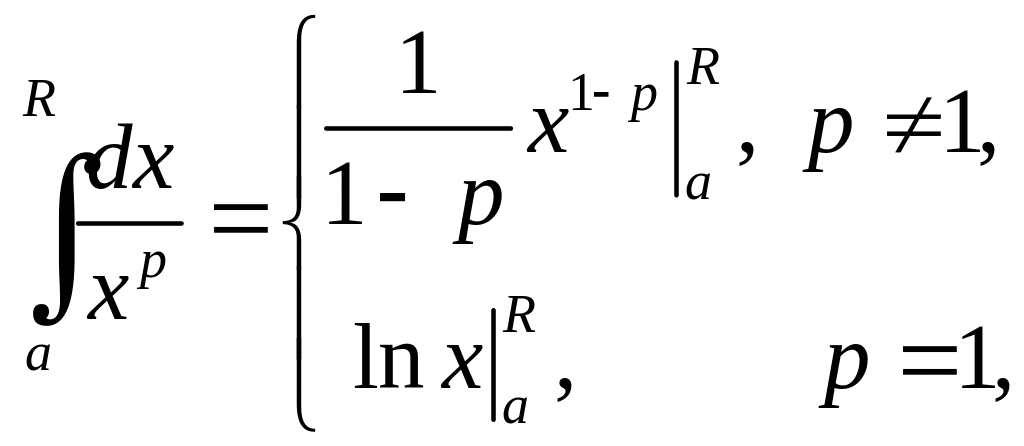
то границя

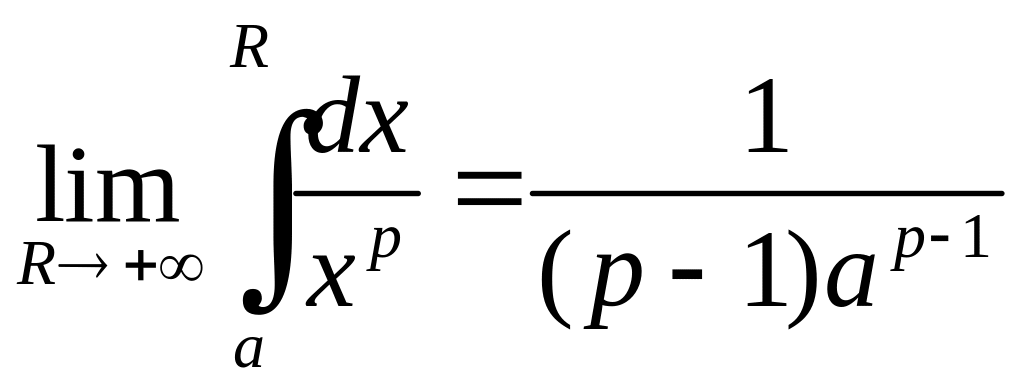
існує тільки при . Таким чином,

, , ,

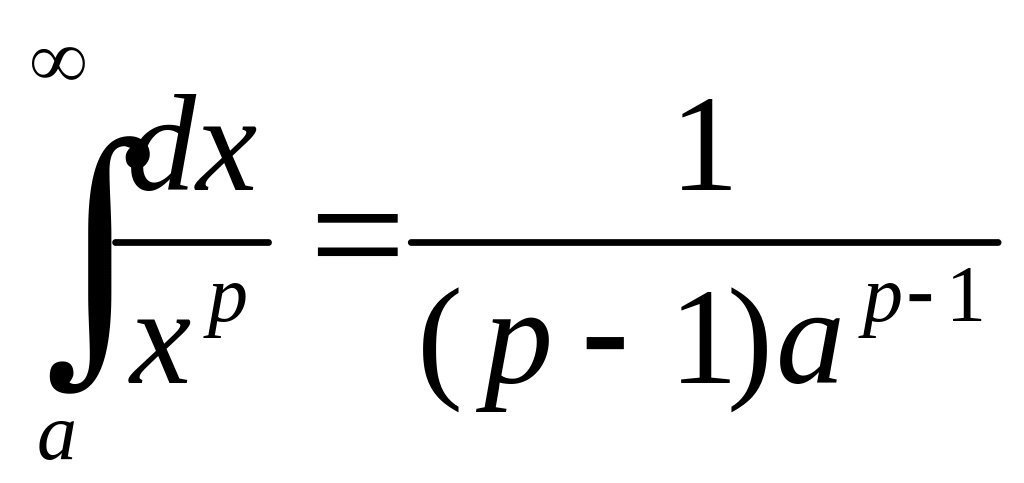а при других значеннях параметра інтеграл (1.2) розбігається, тобто не визначається.

Неважко зрозуміти, що символом 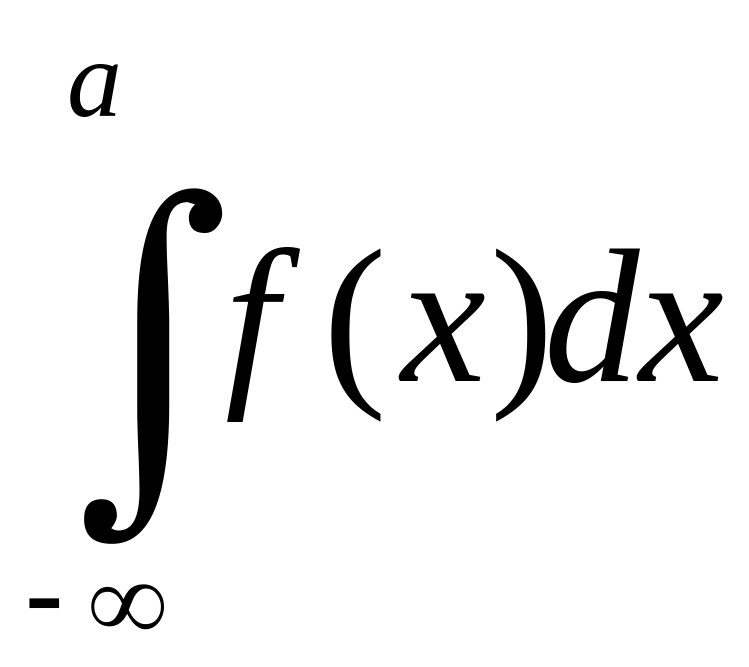позначають границю

,

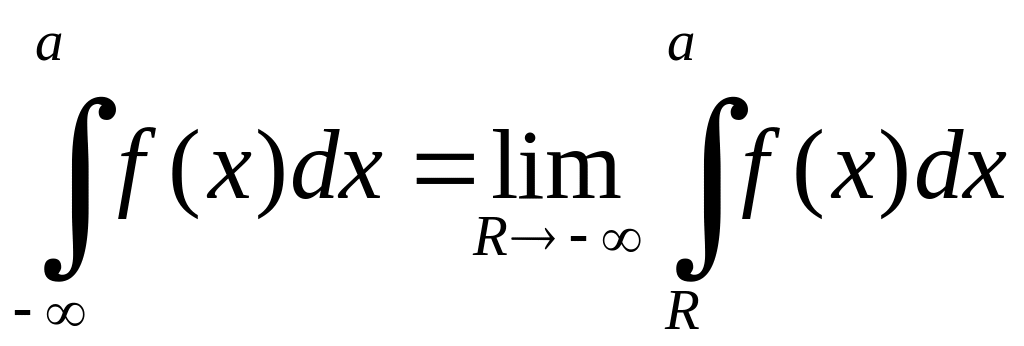де за умовою функція інтегрована на будь-якому проміжку .

За означенням

,

де невласний інтеграл зліва збігається тільки тоді, коли існують обидві границі справа в (1.4).

Таким чином, невласний інтеграл 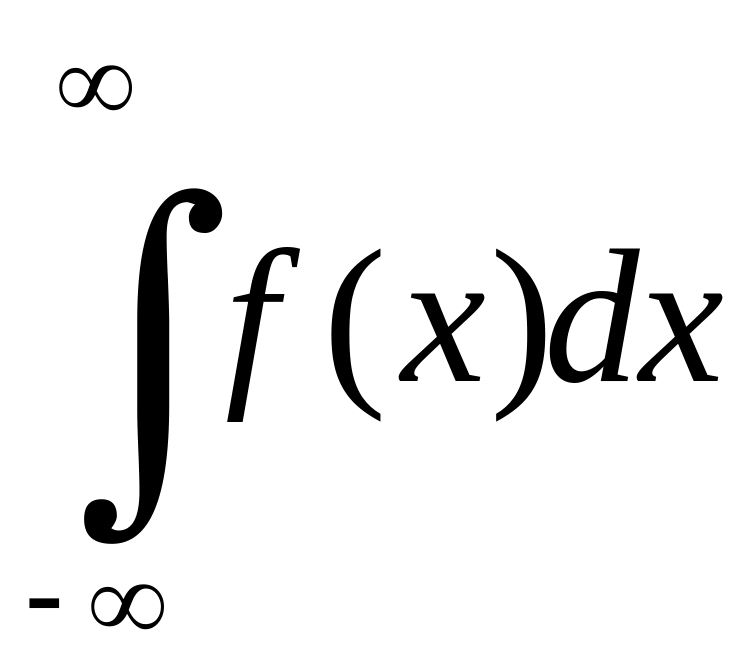збігається, якщо збігаються невласні інтеграли та 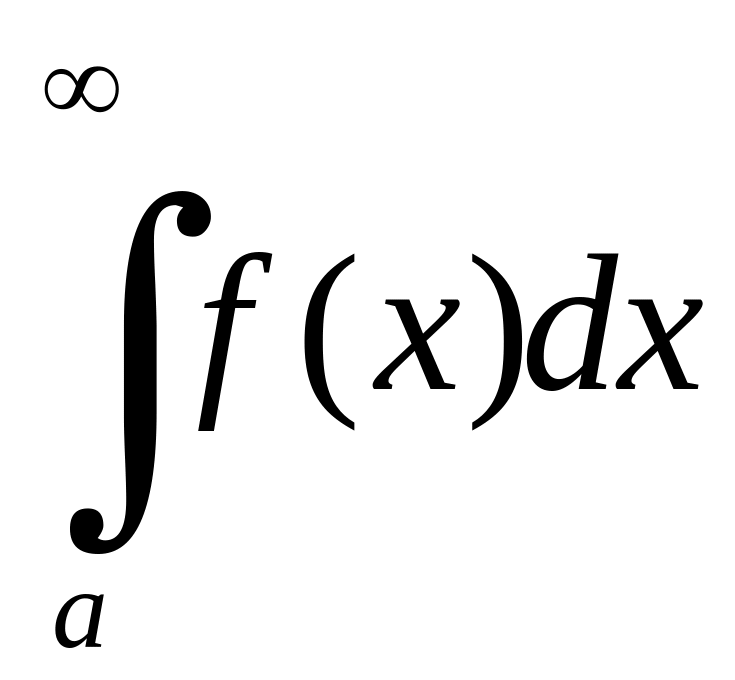. Часто беруть рівним 0.

Приклад 1.2. Дослідити на збіжність

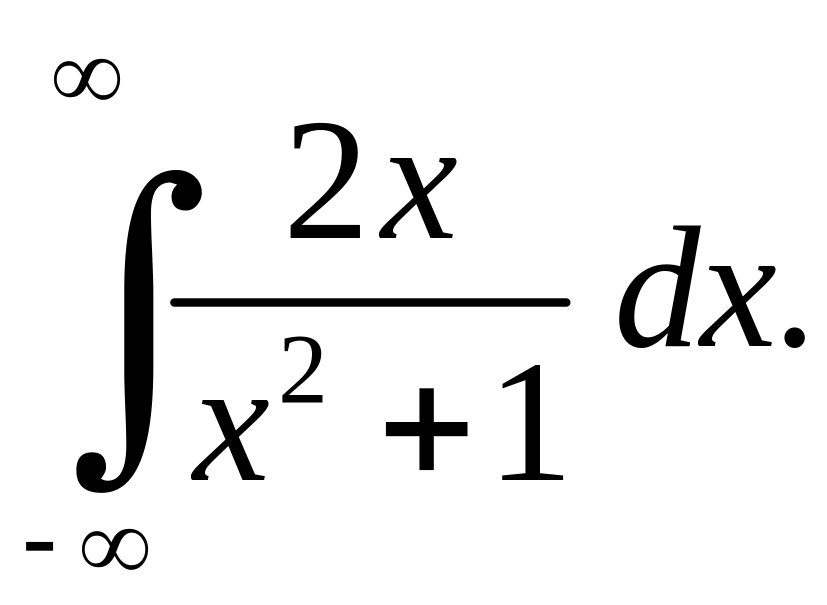
Розв'язання. Розглянемо інтеграл

,

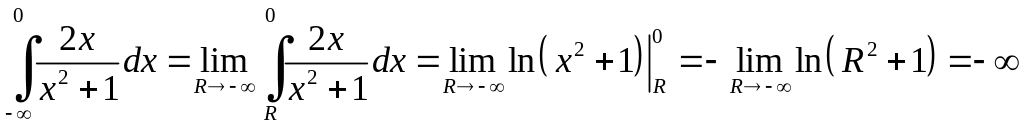а тому невласний інтеграл 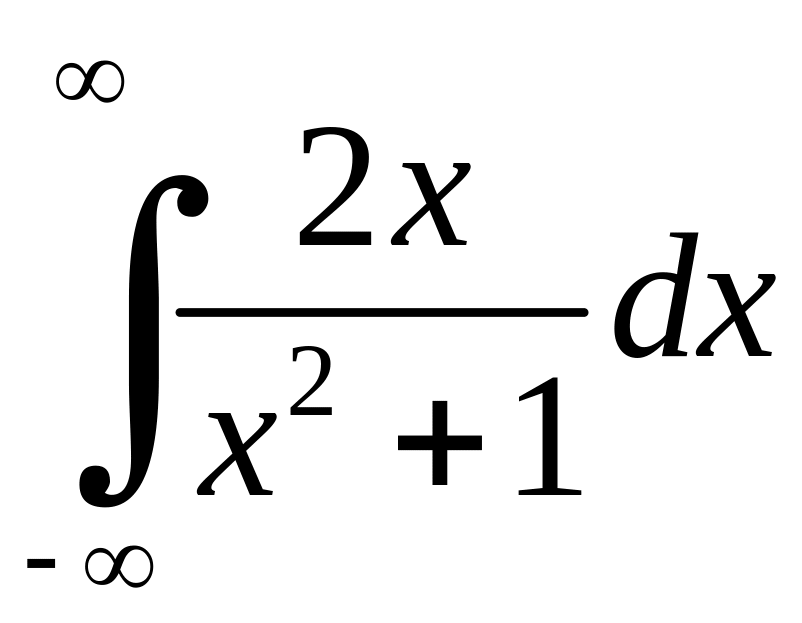розбігається.

Приклад 1.3. Дослідити на збіжність .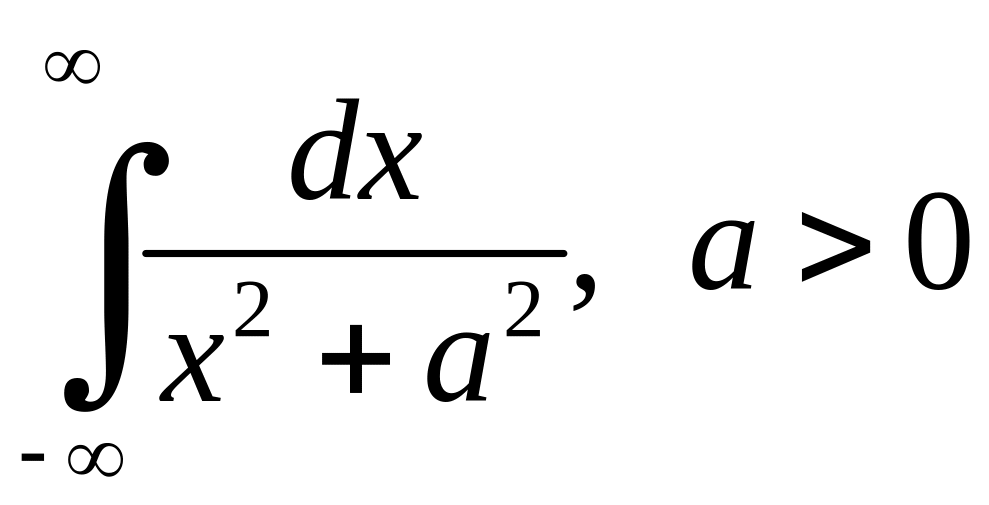

Розв'язання. Окремо розглянемо невласні інтеграли та :

.

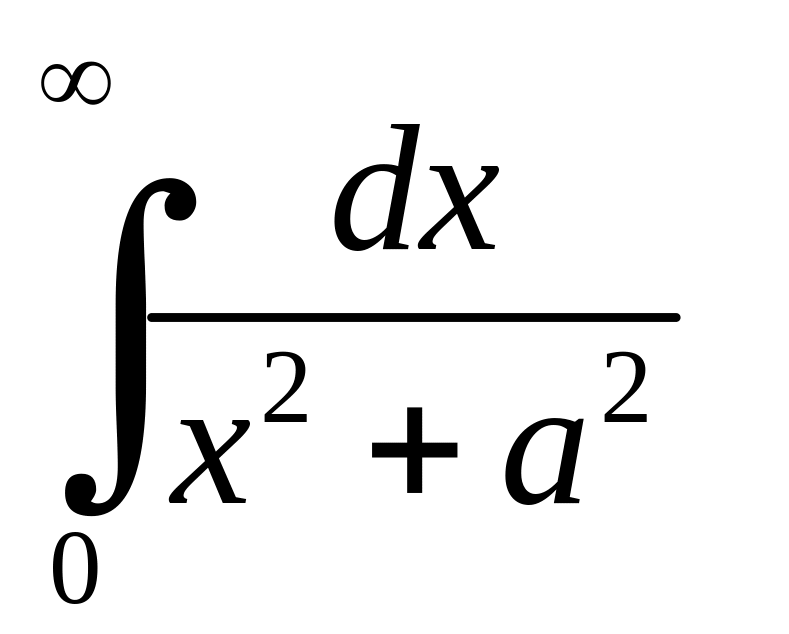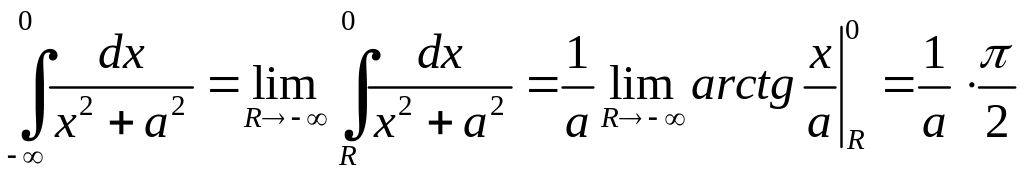Аналогічно,

.

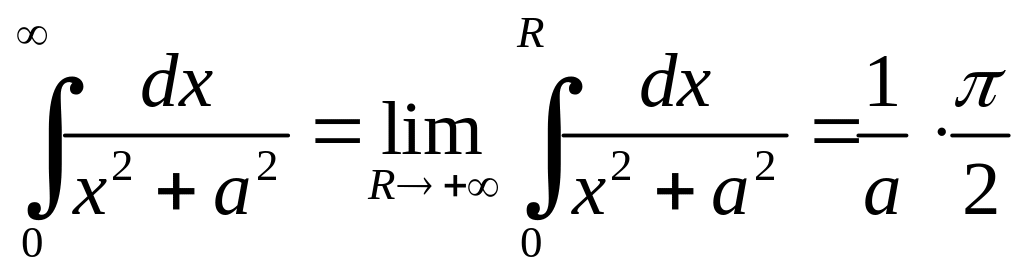Отже, невласний інтеграл 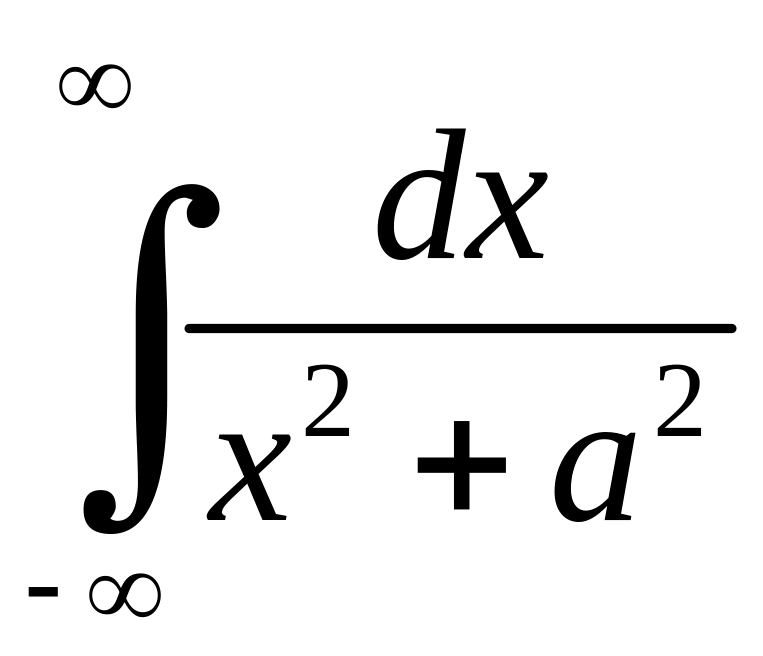збігається і його величина дорівнює :

, .

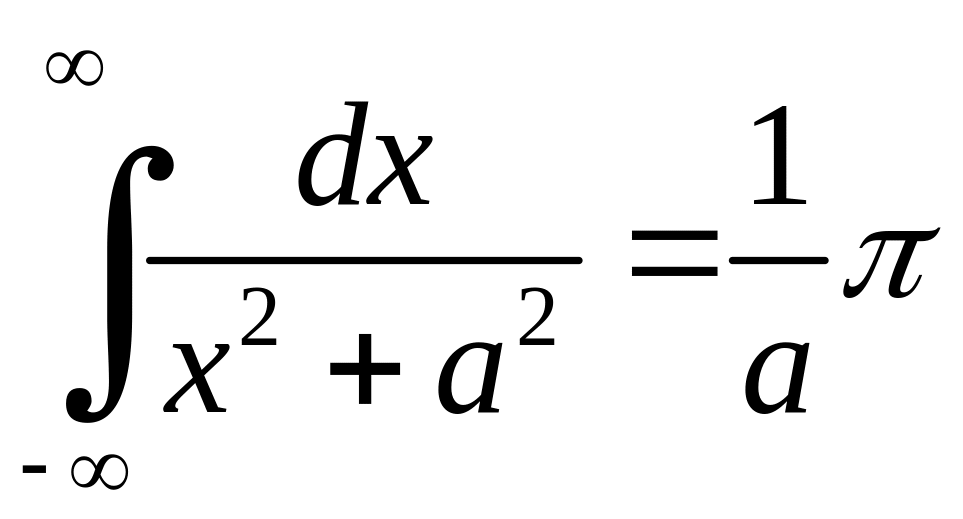Приклад 1.4. Дослідити .

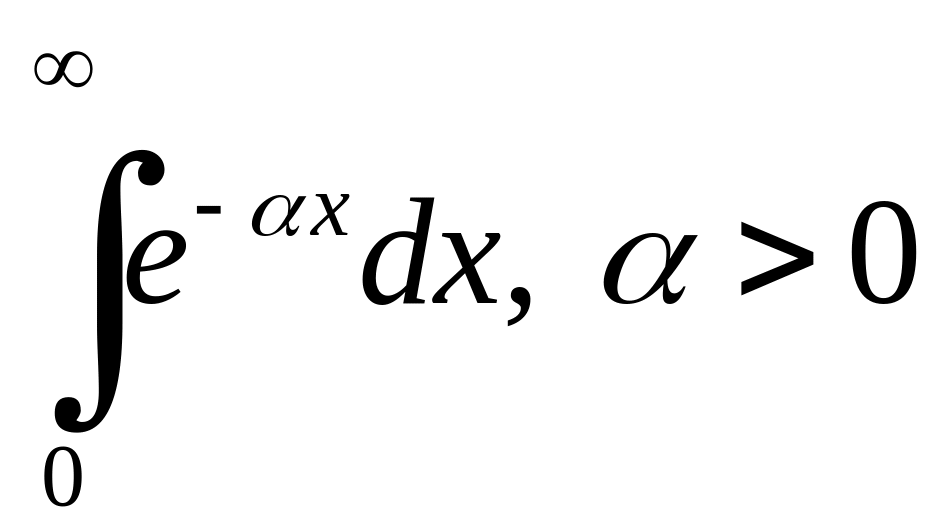Розв'язання. За означенням

.

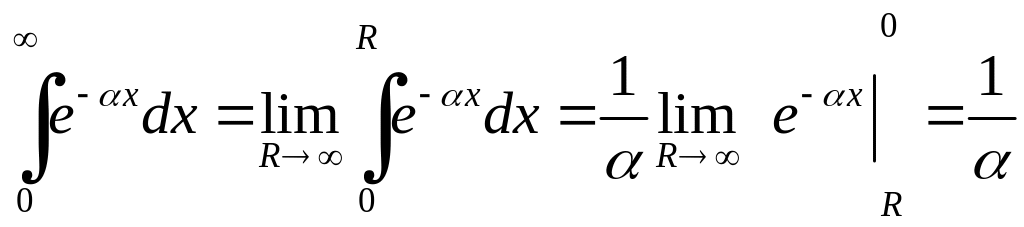Отже, невласний інтеграл збігається і його величина дорівнює .

Відмітимо, що невласний інтеграл (1.2) (а також (1.3)) досліджували в два етапи: спочатку знаходили визначений інтеграл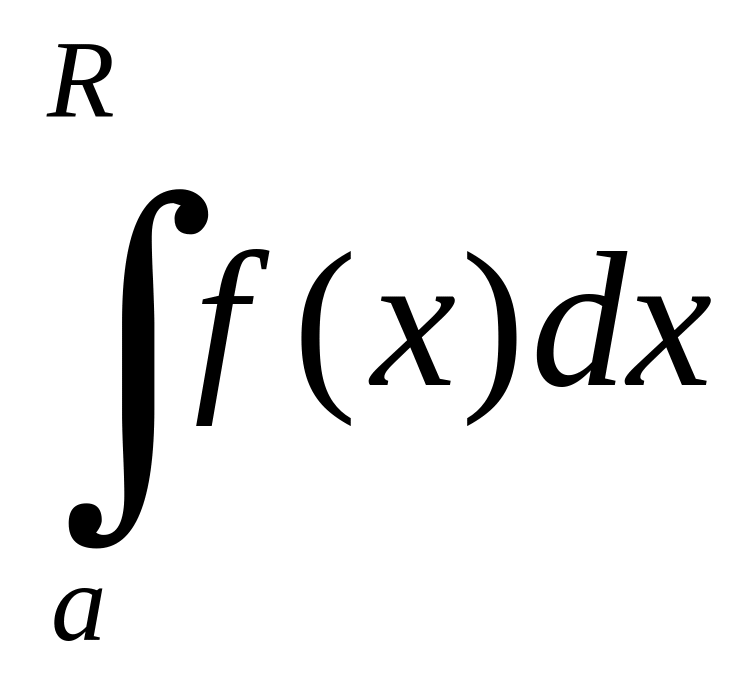 , а потім виконували граничний перехід. Якщо існує первісна для функції на всьому проміжку , то, як правило, пишуть

,

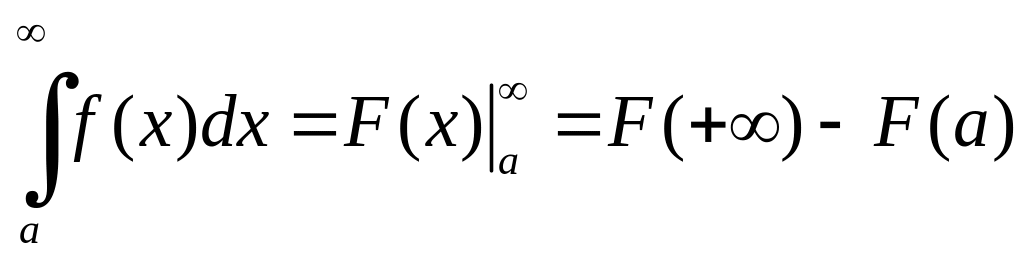де . При цьому маємо на увазі, що границя існує.

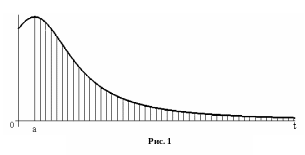
Якщо , то інтеграл , за умовою, що він збігається, допускає геометричну інтерпретацію: його величина визначає площу фігури, обмеженої графіком функції , прямою і віссю (рис.1).

Приклад 1.5. Обчислимо площу фігури, обмеженої графіком функції та віссю .

Розв'язання.

.

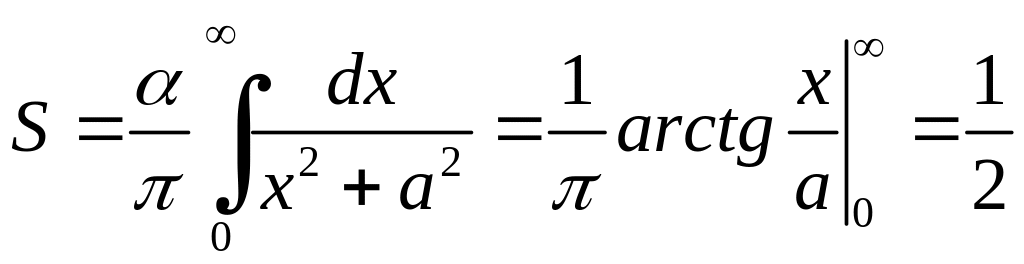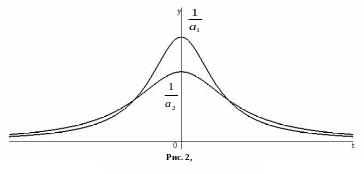
Отже, площа фігури дорівнює . Функцію називають функцією Коші і її графік в залежності від параметра зображений на рисунку (рис. 2).

Означення 2. Нехай функція визначена на проміжку і інтегрована на будь-якому проміжку . Величина

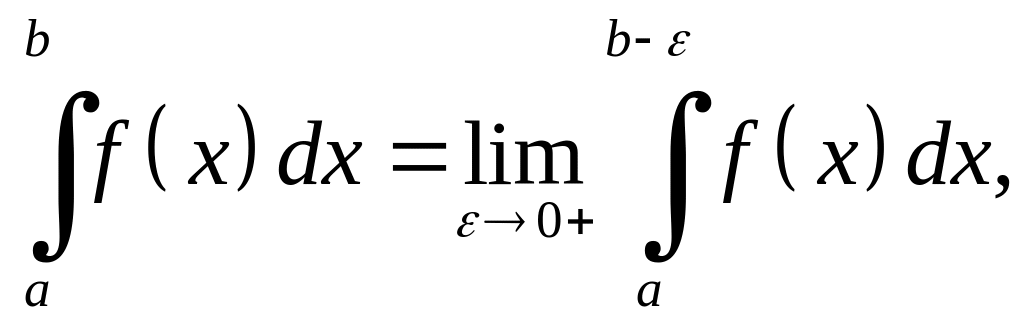
якщо вказана границя існує, називається невласним інтегралом від функції на проміжку або невласним інтегралом другого роду.

Із означення слідує, що в будь-якому околі точки функція може бути необмеженою.

Аналогічно, якщо функція необмежена в околі точки , але інтегрована на відрізку , де довільне (досить мале) число, то невласний інтеграл від функції на проміжку розуміють як границю

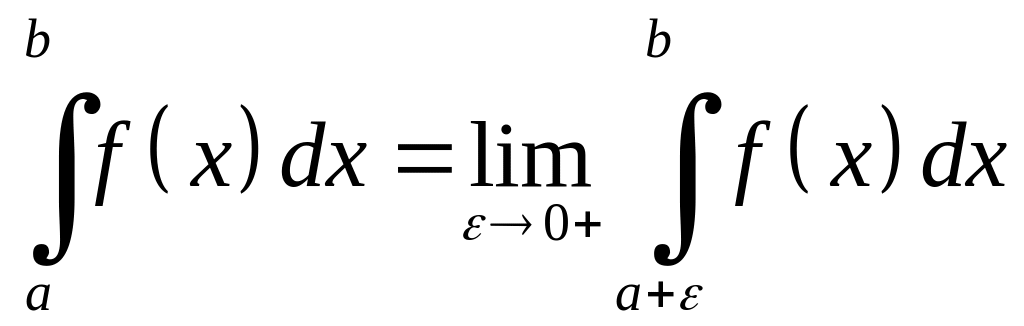
Якщо функція необмежена в околі точки , то за означенням маємо

,

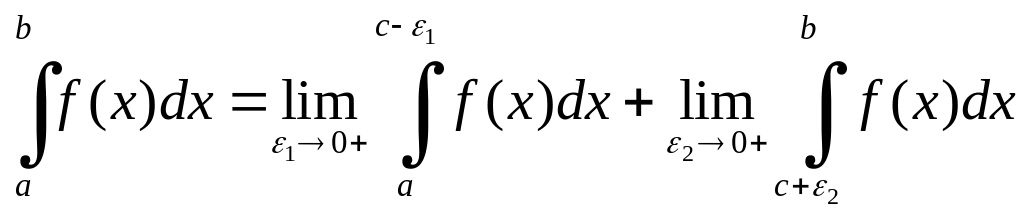причому зліва невласний інтеграл від функції буде визначений тільки, коли існують обидві границі справа в (1.7).

Приклад 1.6. Дослідити, при яких значеннях параметра збігається інтеграл

,

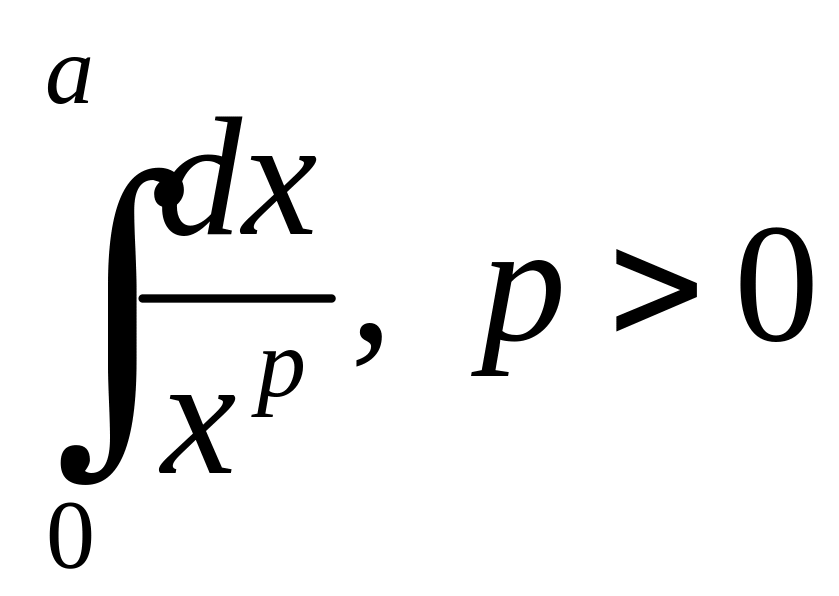Розв'язання. Оскільки функція необмежена в околі точки , коли і

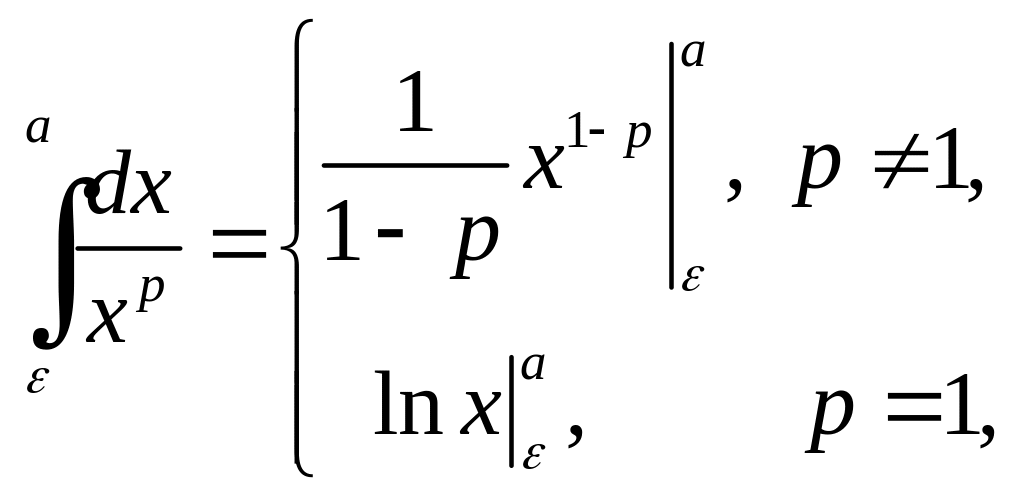
то границя

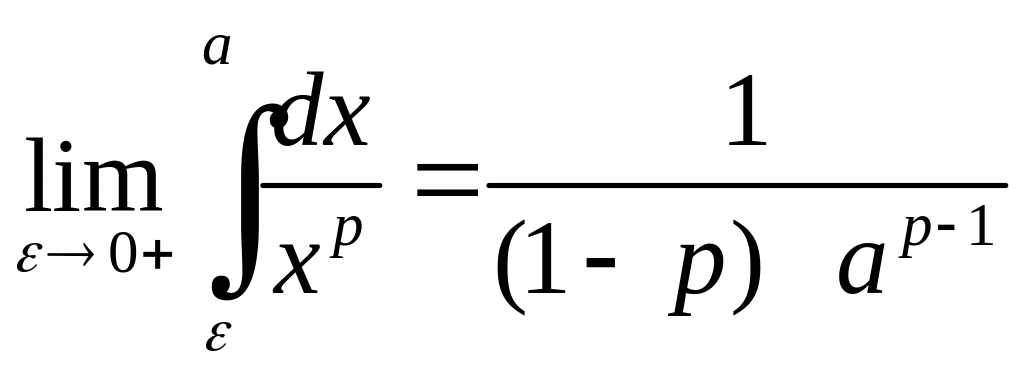
існує тільки при .

Отже, інтеграл (1.8) визначається тільки при .

Приклад 1.7. Обчислити інтеграл .

Розв'язання. Такий інтеграл не визначається, оскільки

.

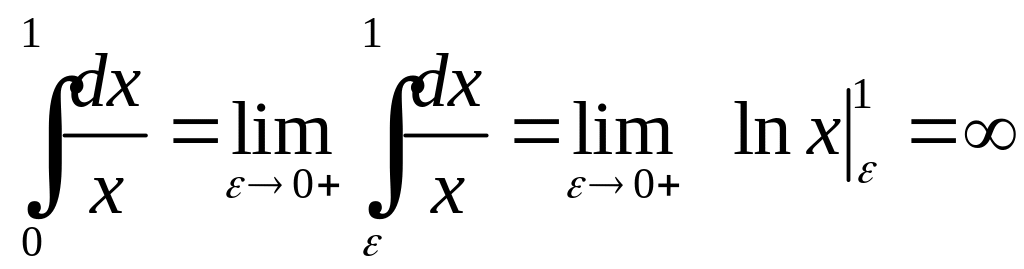Приклад 1.8. Функція обмежена на будь-якому проміжку , але . Розглянемо невласний інтеграл

.

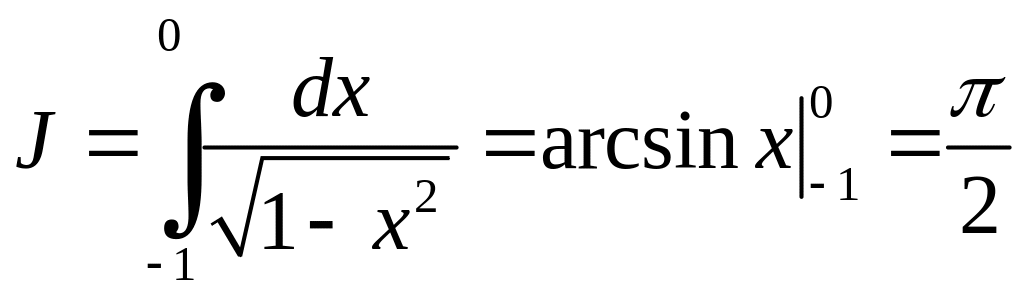Інтеграл збігається і його значення дорівнює . При цьому первісна для функції 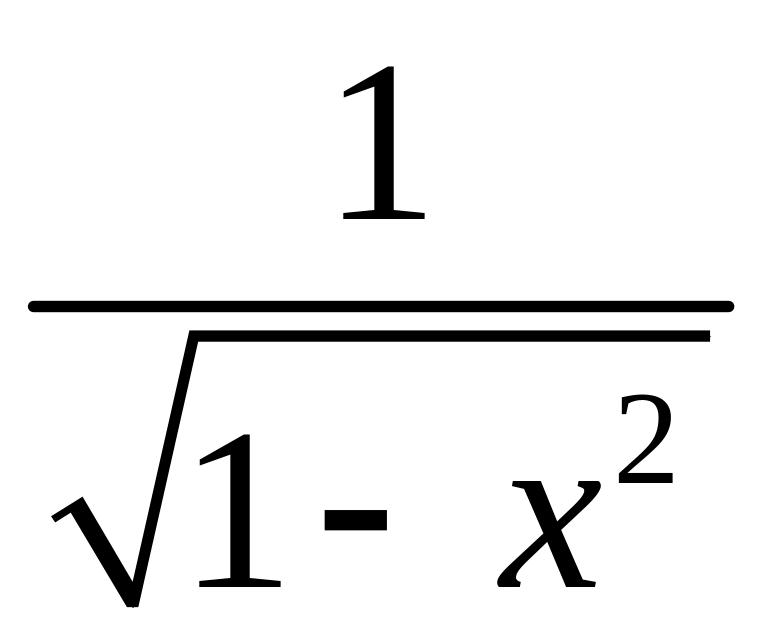неперервна справа в точці .

Отже, якщо в особій точці (або ) існує границя (або ), то будемо писати

.
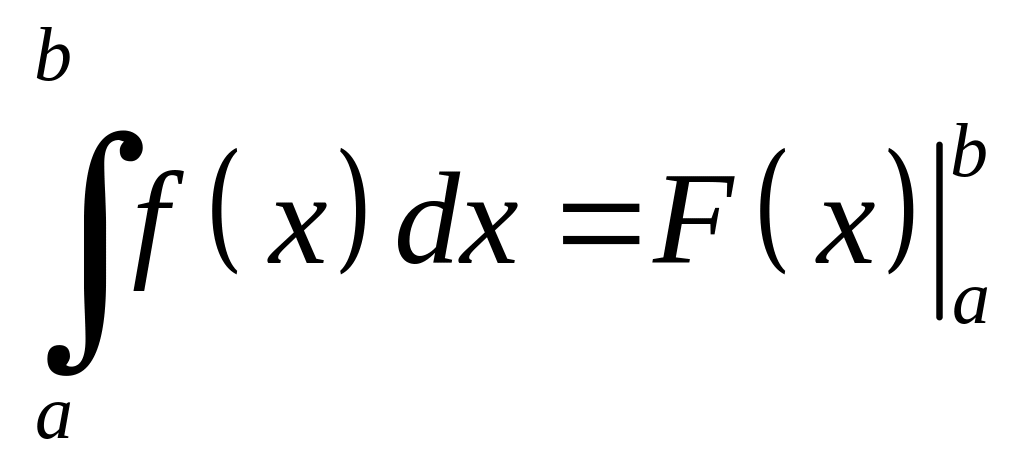